湖北省襄阳市枣阳市吴店镇第二中学2023-2024学年九年级下学期数学期中试题
试卷更新日期:2024-05-14 类型:期中考试
一、选择题(每小题3分,共30分)
-
1. 在 , ,0, 这四个数中,为无理数的是 ( )A、 B、 C、0 D、2. 几何体中,俯视图是三角形的是( )A、
 B、
B、 C、
C、 D、
D、 3. “五一”假期,宜昌旅游市场接待游客万人次,实现旅游总收入亿元.数据“亿”用科学记数法表示为( ).A、 B、 C、 D、4. 下列计算正确的是( )A、 B、 C、 D、5. 下列说法正确的是( )A、“三角形的外角和是360°”是不可能事件 B、调查某批次汽车的抗撞击能力适合用全面调查 C、了解北京冬奥会的收视率适合用抽样调查 D、从全校1500名学生中抽取100名调查了解寒假阅读情况,抽取的样本容量为15006. 把抛物线y=﹣2x2先向右平移1个单位长度,再向上平移2个单位长度后,所得函数的表达式为( )A、y=﹣2(x+1)2+2 B、y=﹣2(x+1)2﹣2 C、y=﹣2(x﹣1)2+2 D、y=﹣2(x﹣1)2﹣27. 若 且 ,则函数 的图象可能是( )A、
3. “五一”假期,宜昌旅游市场接待游客万人次,实现旅游总收入亿元.数据“亿”用科学记数法表示为( ).A、 B、 C、 D、4. 下列计算正确的是( )A、 B、 C、 D、5. 下列说法正确的是( )A、“三角形的外角和是360°”是不可能事件 B、调查某批次汽车的抗撞击能力适合用全面调查 C、了解北京冬奥会的收视率适合用抽样调查 D、从全校1500名学生中抽取100名调查了解寒假阅读情况,抽取的样本容量为15006. 把抛物线y=﹣2x2先向右平移1个单位长度,再向上平移2个单位长度后,所得函数的表达式为( )A、y=﹣2(x+1)2+2 B、y=﹣2(x+1)2﹣2 C、y=﹣2(x﹣1)2+2 D、y=﹣2(x﹣1)2﹣27. 若 且 ,则函数 的图象可能是( )A、 B、
B、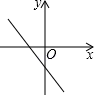 C、
C、 D、
D、 8. 对于反比例函数 , 下列说法不正确的是( )A、图象分布在第二、四象限 B、图象关于原点对称 C、图象经过点(1,) D、若点 , 都在该函数图象上,且 , 则9. 如图,四边形ABCD内接于⊙O,若四边形ABCO是平行四边形,则∠ADC的大小为( )
8. 对于反比例函数 , 下列说法不正确的是( )A、图象分布在第二、四象限 B、图象关于原点对称 C、图象经过点(1,) D、若点 , 都在该函数图象上,且 , 则9. 如图,四边形ABCD内接于⊙O,若四边形ABCO是平行四边形,则∠ADC的大小为( ) A、45° B、50° C、60° D、75°10. 如图,已知抛物线 的对称轴为直线 .给出下列结论:
A、45° B、50° C、60° D、75°10. 如图,已知抛物线 的对称轴为直线 .给出下列结论: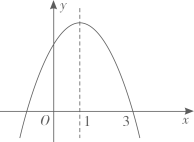
① ; ② ; ③ ; ④ .
其中,正确的结论有( )
A、1个 B、2个 C、3个 D、4个二、填空题(每小题3分,共15分)
-
11. 已知一元二次方程的两个实数根为 , 若 , 则实数 .12. 在“庆五四·展风采”的演讲比赛中,7位同学参加决赛,演讲成绩依次为:77,80,79,77,80,79,80.这组数据的中位数是 .13. 不等式组的解集为 .14. 某校团支部组织部分共青团员开展学雷锋志愿者服务活动,每个志愿者都可以从以下三个项目中任选一项参加:①敬老院做义工;②文化广场地面保洁;③路口文明岗值勤.则小明和小慧选择参加同一项目的概率是 .15. 如图,在正方形ABCD中,E是CD边上一点,将△ADE沿AE翻折至△AD'E , 延长ED',交BC于点F . 若AB=15,DE=10,则tan∠EFC的值是 .

三、解答题(本大题共9个小题,共75分)
-
16. 计算: .17. 如图,在 中, , .
 (1)、通过观察尺规作图的痕迹,可以发现直线 是线段 的 , 射线 是 的;(2)、在(1)所作的图中,求 的度数.18. 某工厂现在平均每天比原计划多生产50台机器,现在生产600台机器所需时间与原计划生产450机器所需时间相同,求该工厂原来平均每天生产多少台机器?19. 如图,矩形的对角线 , 相交于点O, .
(1)、通过观察尺规作图的痕迹,可以发现直线 是线段 的 , 射线 是 的;(2)、在(1)所作的图中,求 的度数.18. 某工厂现在平均每天比原计划多生产50台机器,现在生产600台机器所需时间与原计划生产450机器所需时间相同,求该工厂原来平均每天生产多少台机器?19. 如图,矩形的对角线 , 相交于点O, . (1)、求证:四边形是菱形;(2)、若 , 求四边形的面积.20. 如图,一次函数与反比例函数的图像在第一、第三象限分别交于 , 两点,连接、 .
(1)、求证:四边形是菱形;(2)、若 , 求四边形的面积.20. 如图,一次函数与反比例函数的图像在第一、第三象限分别交于 , 两点,连接、 . (1)、求一次函数和反比例函数解析式;(2)、求的面积;(3)、观察不等式的解集为: .21. 如图,是的直径,点E , C在上,点C是的中点,垂直于过C点的直线 , 垂足为D , 的延长线交直线于点F .
(1)、求一次函数和反比例函数解析式;(2)、求的面积;(3)、观察不等式的解集为: .21. 如图,是的直径,点E , C在上,点C是的中点,垂直于过C点的直线 , 垂足为D , 的延长线交直线于点F . (1)、求证:是的切线;(2)、若 , , ①求的半径;②求线段的长.22. “五一”前夕,某超市销售一款商品,进价每件75元,售价每件140元,每天销售40件,每销售一件需支付给超市管理费5元.从五月一日开始,该超市对这款商品开展为期一个月的“每天降价1元”的促销活动,即从第一天(5月1日)开始每天的售价均比前一天降低1元.通过市场调查发现,该商品的日销售量y(件)与第x天( , 且x为整数)之间存在一次函数关系,x , y之间的部分数值对应关系如下表:
(1)、求证:是的切线;(2)、若 , , ①求的半径;②求线段的长.22. “五一”前夕,某超市销售一款商品,进价每件75元,售价每件140元,每天销售40件,每销售一件需支付给超市管理费5元.从五月一日开始,该超市对这款商品开展为期一个月的“每天降价1元”的促销活动,即从第一天(5月1日)开始每天的售价均比前一天降低1元.通过市场调查发现,该商品的日销售量y(件)与第x天( , 且x为整数)之间存在一次函数关系,x , y之间的部分数值对应关系如下表:第x天
5
10
15
20
日销售量y(件)
50
60
70
80
(1)、直接写出y与x的函数关系式;(2)、设第x天的利润为W元,试求出W与x之间的函数关系式,并求出哪一天的利润最大?最大利润是多少元?(3)、销售20天后,由于某种原因,该商品的进价从第21天开始每件下降4元,其他条件保持不变,求超市在这一个月中,该商品的日销售利润不低于3430元的共有多少天?23.(1)、如图1,在中, , 点分别在边上,且 , 若 , 则的值是; (2)、如图2,在(1)的条件下,将绕点A逆时针方向旋转一定的角度,连接和 , 的值变化吗?若变化,请说明理由;若不变化,请求出不变的值;
(2)、如图2,在(1)的条件下,将绕点A逆时针方向旋转一定的角度,连接和 , 的值变化吗?若变化,请说明理由;若不变化,请求出不变的值; (3)、如图3,在中, , , 点分别在边上,且 , 现将绕点A逆时针方向旋转到位置,连接和 , 若 , 请直接写出线段的长.
(3)、如图3,在中, , , 点分别在边上,且 , 现将绕点A逆时针方向旋转到位置,连接和 , 若 , 请直接写出线段的长. 24. 在平面直角坐标系中,已知抛物线与x轴交于点两点,与y轴交于点 , 点P是抛物线上的一个动点.
24. 在平面直角坐标系中,已知抛物线与x轴交于点两点,与y轴交于点 , 点P是抛物线上的一个动点. (1)、求抛物线的表达式;(2)、当点P在直线上方的抛物线上时,连接交于点D.如图1.当的值最大时,求点P的坐标及的最大值;(3)、过点P作x轴的垂线交直线于点M,连接 , 将沿直线翻折,当点M的对应点恰好落在y轴上时,请直接写出此时点M的坐标.
(1)、求抛物线的表达式;(2)、当点P在直线上方的抛物线上时,连接交于点D.如图1.当的值最大时,求点P的坐标及的最大值;(3)、过点P作x轴的垂线交直线于点M,连接 , 将沿直线翻折,当点M的对应点恰好落在y轴上时,请直接写出此时点M的坐标.