(通用版)2024年中考数学重点知识冲刺训练---不等式与不等式组
试卷更新日期:2024-05-14 类型:三轮冲刺
一、选择题
-
1. 小霞原有存款52元,小明原有存款70元从这个月开始,小霞每月存15元零花钱,小明每月存12元零花钱,设经过n个月后小霞的存款超过小明,可列不等式为( )A、52+15n>70+12n B、52+15n<70+12n C、52+12n>70+15n D、52+12n<70+15n2. 若 , 则下列不等式一定成立的是( )A、 B、 C、 D、3. 不等式组的解在数轴上表示正确的是( )A、
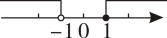 B、
B、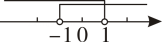 C、
C、 D、
D、 4. 已知 , 则一定有 , “”中应填的符号是( )A、> B、< C、 D、5. 关于的一元一次不等式的解集在数轴上的表示如图所示,则的值为( )
4. 已知 , 则一定有 , “”中应填的符号是( )A、> B、< C、 D、5. 关于的一元一次不等式的解集在数轴上的表示如图所示,则的值为( ) A、3 B、2 C、1 D、06. 关于x的一元一次不等式的解集为( )A、x B、x C、x D、x7. 如图,数轴上的点A和点B分别在原点的左侧和右侧,点A、B对应的实数分别是a、b,下列结论一定成立的是( )
A、3 B、2 C、1 D、06. 关于x的一元一次不等式的解集为( )A、x B、x C、x D、x7. 如图,数轴上的点A和点B分别在原点的左侧和右侧,点A、B对应的实数分别是a、b,下列结论一定成立的是( )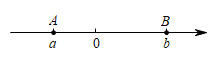 A、 B、 C、 D、8. 若关于x的不等式组的解集是 , 则a的取值范围是( )A、 B、 C、 D、9. 如图,函数 的图象经过点 ,与函数 的图象交于点 ,则不等式 的解集为( )
A、 B、 C、 D、8. 若关于x的不等式组的解集是 , 则a的取值范围是( )A、 B、 C、 D、9. 如图,函数 的图象经过点 ,与函数 的图象交于点 ,则不等式 的解集为( )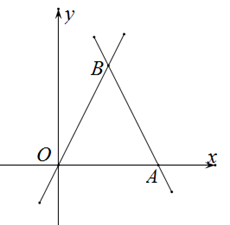 A、 B、 C、 D、10. 如图,将一枚跳棋放在七边形ABCDEFG的顶点A处,按顺时针方向移动这枚跳棋2020次.移动规则是:第k次移动k个顶点(如第一次移动1个顶点,跳棋停留在B处,第二次移动2个顶点,跳棋停留在D处),按这样的规则,在这2020次移动中,跳棋不可能停留的顶点是( )
A、 B、 C、 D、10. 如图,将一枚跳棋放在七边形ABCDEFG的顶点A处,按顺时针方向移动这枚跳棋2020次.移动规则是:第k次移动k个顶点(如第一次移动1个顶点,跳棋停留在B处,第二次移动2个顶点,跳棋停留在D处),按这样的规则,在这2020次移动中,跳棋不可能停留的顶点是( )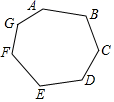 A、C、E B、E、F C、G、C、E D、E、C、F
A、C、E B、E、F C、G、C、E D、E、C、F二、填空题
-
11. 不等式组的解集是 .12. 用一组 , , 的值说明命题“若 ,则 ”是错误的,这组值可以是 , , .13. 某商品进价4元,标价5元出售,商家准备打折销售,但其利润率不能少于10%,则最多可打折.14. 经历了漫长艰难的体训,初三学子即将迎来中考体考,初三某班的家长为孩子们准备了脉动饮料、士力架和葡萄糖口服液.已知脉动饮料、士力架和葡萄糖口服液的单价之和为22元,计划购买脉动饮料、士力架和葡萄糖口服液的数量总共不超过200,其中葡萄糖口服液的单价为10元,计划购买50支.脉动饮料的数量不多于士力架数量的一半,但至少购买30瓶.在做预算时,将脉动饮料和士力架的单价弄反了,结果在实际购买时,总费用比预算多了160元.若脉动饮料、士力架和葡萄糖口服液的单价均为整数,则实际购买脉动饮料、士力架和葡萄糖口服液的总费用最多需要花费元.
三、解答题
-
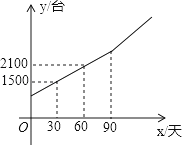
15. 解不等式组 ,并写出满足不等式组的所有整数解.16. 对于任意实数 , ,定义关于“ ”的一种运算如下: .例如: ,(1)、若 ,求 的值;(2)、若 ,求 的取值范围.17. 某班为了丰富学生的课外活动和体育健身,计划购买10个足球和20根跳绳,共花费980元,其中足球的价格是跳绳价格的3倍多8元.(1)、求跳绳和足球的单价;(2)、在实际课外活动中,发现如果全班同学根据自身的爱好总有部分学生无法玩足球或跳绳,若使用剩余班费233元,并要求至少购买一个足球,那么最多可购买多少根跳绳?18. 为丰富学生课余生活,提高学生运算能力,数学小组设计了如下的解题接力游戏:(1)、解不等式组:;(2)、当m取(1)的一个整数解时,解方程.19. 佳衣服装厂给某中学用同样的布料生产 , 两种不同款式的服装,每套款服装所用布料的米数相同,每套款服装所用布料的米数相同,若套款服装和套款服装需用布料米,套款服装和套款服装需用布料米.(1)、求每套款服装和每套款服装需用布料各多少米;(2)、该中学需要 , 两款服装共套,所用布料不超过米,那么该服装厂最少需要生产多少套款服装?20. 随着生活质量的提高,人们健康意识逐渐增强,安装净水设备的百姓家庭越来越多.某厂家从去年开始投入生产净水器,生产净水器的总量y(台)与今年的生产天数x(天)的关系如图所示.今年生产90天后,厂家改进了技术,平均每天的生产数量达到30台.
(1)求y与x之间的函数表达式;
(2)已知该厂家去年平均每天的生产数量与今年前90天平均每天的生产数量相同,求厂家去年生产的天数;
(3)如果厂家制定总量不少于6000台的生产计划,那么在改进技术后,至少还要多少天完成生产计划?
四、综合题
-
21. 倡导健康生活,推进全民健身,某社区要购进A,B两种型号的健身器材若干套,A,B两种型号健身器材的购买单价分别为每套310元,460元,且每种型号健身器材必须整套购买.(1)、若购买A,B两种型号的健身器材共50套,且恰好支出20000元,求A,B两种型号健身器材各购买多少套?(2)、若购买A,B两种型号的健身器材共50套,且支出不超过18000元,求A种型号健身器材至少要购买多少套?22. 李叔叔批发甲、乙两种蔬菜到菜市场去卖,已知甲、乙两种蔬菜的批发价和零售价如下表所示:
品名
甲蔬菜
乙蔬菜
批发价/(元/kg)
零售价/(元/kg)
(1)、若他批发甲、乙两种蔬菜共花元.求批发甲乙两种蔬菜各多少千克?(列方程或方程组求解)(2)、若他批发甲、乙两种蔬菜共花m元,设批发甲种蔬菜 , 求m与n的函数关系式;(3)、在(2)的条件下,全部卖完蔬菜后要保证利润不低于元,至少批发甲种蔬菜多少千克?23. 如图,在平面直角坐标系中,抛物线交轴于点 , 顶点坐标为 . 抛物线交轴于点 , 顶点坐标为 . (1)、连接 , 求线段的长;(2)、点在抛物线上,点在抛物线上.比较大小:;(3)、若点在抛物线上, , 求的取值范围.
(1)、连接 , 求线段的长;(2)、点在抛物线上,点在抛物线上.比较大小:;(3)、若点在抛物线上, , 求的取值范围.