湖南省长沙市浏阳市2023-2024学年八年级下学期数学期中试卷

试卷更新日期：2024-05-14 类型：期中考试

进入出卷网下载

一、选择题：本题共10小题，每小题3分，共30分。在每小题给出的选项中，只有一项是符合题目要求的。

1. 下列各式是最简二次根式的是（）

A、 $\sqrt{\frac{1}{2}}$ B、 $\sqrt{8}$ C、 $\frac{\sqrt{5}}{3}$ D、 $\sqrt{0.6}$

查看试题解析
2. 如图，点 $M (- 3,4)$ 到原点的距离是( )

A、 $3$ B、 $4$ C、 $5$ D、 $7$

查看试题解析
3. 下列计算正确的是( )

A、 $3 \sqrt{2} - \sqrt{2} = \sqrt{2}$ B、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ C、 $\sqrt{3} \times \sqrt{5} = \sqrt{15}$ D、 $\sqrt{6} \div \sqrt{3} = \sqrt{3}$

查看试题解析
4. 如图，为测量池塘边 $A$ 、 $B$ 两点的距离，小宇同学在池塘的一侧选取一点 $O$ ，测得 $O A$ 、 $O B$ 的中点分别是点 $D$ 、 $E$ ，且 $D E = 18$ 米，则 $A$ 、 $B$ 两点的距离是( )

A、 $9$ 米 B、 $18$ 米 C、 $36$ 米 D、 $54$ 米

查看试题解析
5. 如图，平行四边形 $A B C D$ 中，若 $∠ B = 2 ∠ A$ ，则 $∠ C$ 的度数为( )

A、 $30 °$ B、 $40 °$ C、 $50 °$ D、 $60 °$

查看试题解析
6. 如图，已知线段 $A B$ 、 $A D$ 和射线 $B P$ ，且 $A D / / B P$ ，在射线 $B P$ 上找一点 $C$ ，使得四边形 $A B C D$ 是平行四边形，下列作法不一定可行的是( )

A、过点 $D$ 作 $D C / / A B$ 与 $B P$ 交于点 $C$ B、在 $A D$ 下方作 $∠ A D C$ 与 $B P$ 交于点 $C$ ，使 $∠ A D C = ∠ A B P$ C、在 $B P$ 上截取 $B C$ ，使 $B C = A D$ ，连接 $D C$ D、以点 $D$ 为圆心， $A B$ 长为半径画弧，与 $B P$ 交于点 $C$ ，连接 $D C$

查看试题解析
7. 如图，在四边形 $A B C D$ 中， $∠ A B C$ 为直角， $A B / / C D$ ， $A B = C D$ ，对角线 $A C$ 、 $B D$ 相交于点 $O$ ， $A B = 5$ ， $A O = 6.5$ ，则四边形 $A B C D$ 的面积为( )

A、 $60$ B、 $30$ C、 $90$ D、 $96$

查看试题解析
8. 如图， $△ A B C$ 中， $∠ C = 90 °$ ， $A C = 8$ ， $B C = 6$ ，线段 $D E$ 的两个端点 $D$ 、 $E$ 分别在边 $A C$ ， $B C$ 上滑动，且 $D E = 6$ ，若点 $M$ 、 $N$ 分别是 $D E$ 、 $A B$ 的中点，则 $M N$ 的最小值为( )

A、 $2$ B、 $2.5$ C、 $3$ D、 $3.5$

查看试题解析
9. 如图，在 $△ A B C$ 中，点 $D$ ， $E$ ， $F$ 分别在边 $B C$ ， $A B$ ， $A C$ 上，且 $D E / / C A$ ， $D F / / B A$ ，下列说法不正确是( )

A、若 $A D = E F$ ，那么四边形 $A E D F$ 是矩形 B、若 $A D$ 平分 $∠ B A C$ ，那么四边形 $A E D F$ 是菱形 C、若 $A D ⊥ B C$ 且 $A B = A C$ ，那么四边形 $A E D F$ 是菱形 D、若 $∠ A D C = 90 °$ ，那么四边形 $A E D F$ 是矩形

查看试题解析
10. 如图，在矩形纸片 $A B C D$ 中， $A B = 3$ ， $A D = 9$ ，将其折叠，使点 $D$ 与点 $B$ 重合，折痕为 $E F .$ 则 $E F$ 的长为( )

A、 $4$ B、 $\frac{10}{3}$ C、 $2 \sqrt{3}$ D、 $\sqrt{10}$

查看试题解析

二、填空题：本题共6小题，每小题3分，共18分。

11. 要使二次根式 $\sqrt{x - 2024}$ 有意义，实数 $x$ 的取值范围是．

查看试题解析
12. 已知菱形的两条对角线分别是 $4$ 和 $6$ ，则其面积是．

查看试题解析
13. 若 $x$ ， $y$ 为实数，且 $\sqrt{x - 3} + (y + 2)^{2} = 0$ ，则 $x y =$ ．

查看试题解析
14. 古今中外的不少学者对三角形面积的计算做出了诸多思考，尤其值得一提的是古希腊几何学家海伦和我国南宋数学家秦九韶均提出了类似的计算办法：若三角形三边长分别为相 $a$ 、 $b$ 、 $c$ ，记 $p = \frac{a + b + c}{2}$ ，则三角形的面积为 $s = \sqrt{p (p - a) (p - b) (p - c)}$ ，因此后人将他们的发现合称为海伦 $-$ 秦九韶公式，请你利用海伦 $-$ 秦九韶公式计算以下 $△ A B C$ 的面积为．

查看试题解析
15. 如图，我国古代数学家赵爽的“勾股图”是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形 $.$ 如果大正方形的面积是 $12$ ，小正方形的面积是 $3$ ，直角三角形的两直角边分别为 $a$ ， $b$ ，那么 $a + b$ 的值是．

查看试题解析
16. 如图所示的网格是正方形网格，则 $∠ D A B + ∠ D B A =$ $° . ($ 点 $D$ ， $A$ ， $B$ 是网格线交点 $)$

查看试题解析

三、解答题：本题共9小题，共72分。解答应写出文字说明，证明过程或演算步骤。

17. 计算：

(1)、 $\sqrt{18} - \sqrt{32}$ ；

(2)、 $2 \sqrt{12} \times \frac{\sqrt{3}}{4}$ ．

查看试题解析
18. 如图，在 $△ A B C$ 中， $A B = A C$ ， $D$ 为边 $B C$ 上一点，以 $A B$ ， $B D$ 为邻边作平行四边形 $A B D E$ ，连接 $A D$ 、 $C E$ ．

(1)、求证： $△ A C D$ ≌ $△ E D C$ ；

(2)、若点 $D$ 是 $B C$ 中点，说明四边形 $A D C E$ 是矩形．

查看试题解析
19. 我国古代数学著作《九章算术》中的一个问题．原文是：今有池方一丈，葭生其中央，出水尺．引葭赴岸，适与岸齐问水深、葭长各几何译文大意是：如图，有一个水池，水面是一个边长为10尺的正方形，在水池正中央有一根芦苇，它高出水面1尺．如果把这根芦苇拉向水池边的中点，它的顶端恰好到达池边的水面．问水的深度与这根芦苇的长度分别是多少？

查看试题解析
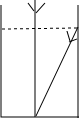20. 先化简，再求值： $a + \sqrt{1 - 2 a + a^{2}}$ ，其中 $a = 1007 .$ 如图是小亮和小芳的解答过程．

(1)、的解法是错误的；

(2)、错误的原因在于未能正确地运用二次根式的性质：；

(3)、先化简，再求值： $a + 2 \sqrt{a^{2} - 6 a + 9}$ ，其中 $a = - 2024$ ．

查看试题解析
21. 如图，每个小正方形的边长都是1， $A$ ， $B$ ， $C$ ， $D$ 均在网格的格点上．

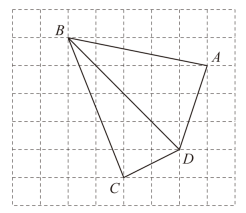(1)、判断 $∠ B C D$ 是否为直角：．（填写“是”或“不是”）

(2)、直接写出四边形 $A B C D$ 的面积为．

(3)、找到格点 $E$ ，并画出四边形 $A B E D$ （一个即可），使得其面积与四边形 $A B C D$ 面积相等．

查看试题解析
22. 如图，在 $△ A B C$ 中， $D$ 是 $B C$ 的中点， $E$ 是 $A D$ 的中点，过点 $A$ 作 $A F / / B C$ ， $A F$ 与 $C E$ 的延长线相交于点 $F$ ，连接 $B F$ ．

(1)、求证：四边形 $A F B D$ 是平行四边形；

(2)、当 $△ A B C$ 满足什么条件时，四边形 $A F B D$ 是菱形？请说明理由．

查看试题解析
23. 如图，矩形 $A E B O$ 的对角线 $A B$ 、 $O E$ 交于点 $F$ ，延长 $A O$ 到点 $C$ ，使 $O C = O A$ ，延长 $B O$ 到点 $D$ ，使 $O D = O B$ ，连接 $A D$ 、 $D C$ 、 $B C$ ．

(1)、求证：四边形 $A B C D$ 是菱形．

(2)、若 $O E = 20$ ， $∠ B C D = 60 °$ ，则菱形 $A B C D$ 的面积为．

查看试题解析
24. 如图，四边形 $A B C D$ 是正方形，点 $E$ 是 $B C$ 的中点， $∠ A E F = 90 °$ ， $E F$ 交正方形外角的平分线 $C F$ 于 $F .$ 求证： $A E = E F$ ．

查看试题解析
25. 若四边形的一条对角线把四边形分成两个等腰三角形，则这条对角线叫做这个四边形的“巧分线”，这个四边形叫“巧妙四边形”，若一个四边形有两条巧分线，则称为“绝妙四边形”．

(1)、下列四边形一定是巧妙四边形的是； $($ 填序号点 $①$ 平行四边形； $②$ 矩形； $③$ 菱形； $④$ 正方形．

(2)、初步应用
在绝妙四边形 $A B C D$ 中， $A C$ 垂直平分 $B D$ ，若 $∠ B A D = 80 °$ ，则 $∠ B C D =$ ；

(3)、深入研究
如图，在梯形 $A B C D$ 中， $A D / / B C$ ， $A B = A D = C D$ ， $∠ B = 72 °$ ．
求证：梯形 $A B C D$ 是绝妙四边形．

(4)、在巧妙四边形 $A B C D$ 中， $A B = A D = C D$ ， $∠ A = 90 °$ ， $A C$ 是四边形 $A B C D$ 的巧分线，请直接写出 $∠ B C D$ 的度数．

查看试题解析