2024年中考数学精选压轴题之四边形综合探究(二)
试卷更新日期:2024-05-13 类型:三轮冲刺
一、实践探究题
-
1.
 (1)、问题提出
(1)、问题提出如图①,在Rt△ABC中,∠A=90°,AB=3,AC=4,在BC上找一点D , 使得AD将△ABC分成面积相等的两部分,作出线段AD , 并求出AD的长度;
(2)、问题探究如图②,点A、B在直线a上,点M、N在直线b上,且a∥b , 连接AN、BM交于点O , 连接AM、BN , 试判断△AOM与△BON的面积关系,并说明你的理由;
(3)、解决问题如图③,刘老伯有一个形状为筝形OACB的养鸡场,在平面直角坐标系中,O(0,0)、A(4,0)、B(0,4)、C(6,6),是否在边AC上存在一点P , 使得过B、P两点修一道笔直的墙(墙的宽度不计),将这个养鸡场分成面积相等的两部分?若存在,请求出直线BP的表达式;若不存在,请说明理由.
2. 已知四边形是菱形,直线经过点 , 且点右侧的部分在的下方,过点作于点 , 点是直线上一点且在点的右侧,连接 , . (1)、数学思考:
(1)、数学思考:如图①,当的边都在的右侧时,线段之间的数量关系为;
(2)、猜想证明:如图②,当的边分别在的两侧时,(1)中的结论是否依然成立?若成立,请给出证明;若不成立,请说明理由;
(3)、拓展延伸:若菱形的边长为13, , , 请直接写出线段的长.
3. 如图 (1)、【问题发现】
(1)、【问题发现】如图1,在正方形中,为对角线上的动点,过点作的垂线,过点作的垂线,两条垂线交于点 , 连接 , 求证: .
(2)、【类比探究】如图2,在矩形中,为对角线上的动点,过点作的垂线,过点作的垂线,两条垂线交于点 , 且 , 连接 , 求的值.
(3)、【拓展延伸】如图3,在(2)的条件下,将改为直线上的动点,其余条件不变,取线段的中点 , 连接 . 若 , 则当是直角三角形时,求的长.
4. 如图 (1)、问题提出如图(1),在正方形ABCD中,E为AD中点,BF⊥CE,求的值;(2)、问题探究如图(2),在等腰Rt△ABC中,点E为AB的中点,BF⊥CE,求的值.5. 综合与实践
(1)、问题提出如图(1),在正方形ABCD中,E为AD中点,BF⊥CE,求的值;(2)、问题探究如图(2),在等腰Rt△ABC中,点E为AB的中点,BF⊥CE,求的值.5. 综合与实践问题情境:“综合实践课”上,老师画出了如图1所示的矩形 , (其中),P(不与点A重合)是边上的动点,连接点P与边的中点E , 将沿直线翻折得到 , 延长交于点F(点F不与点C重合),作的平分线 , 交矩形的边于点G . 问与的位置关系?
 (1)、数学思考:
(1)、数学思考:请你解答老师提出的问题,并说明理由.
(2)、深入探究:老师将图1中的图形通过几何画板改动为如图2,在点P运动过程中,连接 , 若E , O , G三点共线,点G与点D刚好重合,求n的值.
(3)、若 , 连接 , 当是以为直角边的直角三角形,且点G落在边上时,请直接写出的值.6. 黄金分割是一种最能引起美感的分割比例,具有严格的比例性、艺术性、和谐性,蕴藏着丰富的美学价值,我们知道:如图1,如果 , 那么称点C为线段AB的黄金分割点. (1)、如图1, , 点C在线段AB上,且 , 请直接写出CB与AC的比值是;(2)、如图2,在中, , , , 则 , 在BA上截取 , 则 , 在AC上截取 , 则的值为;(3)、如图3,用边长为a的正方形纸片进行如下操作:对折正方形ABDE得折痕MN , 连接EN , 把边AE折到线段EN上,即使点A的对应点H落在EN上,得到折痕EC , 请证明:C是线段AB的黄金分割点;(4)、如图4,在边长为2的正方形ABCD中,M为对角线BD上一点,点N在边CD上,且 , 当N为线段CD的黄金分割点时, , 连NM , 延长NM交AD于E , 求DEE的长.7. 综合与实践
(1)、如图1, , 点C在线段AB上,且 , 请直接写出CB与AC的比值是;(2)、如图2,在中, , , , 则 , 在BA上截取 , 则 , 在AC上截取 , 则的值为;(3)、如图3,用边长为a的正方形纸片进行如下操作:对折正方形ABDE得折痕MN , 连接EN , 把边AE折到线段EN上,即使点A的对应点H落在EN上,得到折痕EC , 请证明:C是线段AB的黄金分割点;(4)、如图4,在边长为2的正方形ABCD中,M为对角线BD上一点,点N在边CD上,且 , 当N为线段CD的黄金分割点时, , 连NM , 延长NM交AD于E , 求DEE的长.7. 综合与实践【问题情境】
为了研究折纸过程中蕴涵的数学知识,老师发给每位同学完全相同的纸片,纸片形状如图1,在四边形中(), , .

图1
【探究实践】
老师引导同学们在边上任取一点E , 连接 , 将沿翻折,点C的对应点为H , 然后将纸片展平,连接并延长,分别交 , 于点M , G .
老师让同学们探究:当点E在不同位置时,能有哪些发现?
经过思考和讨论,小莹、小明向同学们分享了自己发现.

 (1)、如图2,小莹发现:“当折痕与夹角为时,则四边形是平行四边形.”(2)、如图3,小明发现:“当E是的中点时,延长交于点N , 连接 , 则N是的中点.
(1)、如图2,小莹发现:“当折痕与夹角为时,则四边形是平行四边形.”(2)、如图3,小明发现:“当E是的中点时,延长交于点N , 连接 , 则N是的中点.请你分别判断两人的结论是否正确,并说明理由.
(3)、【拓展应用】如图4,小慧在小明发现的基础上,经过进步思考发现:“延长交于点F . 当给出和的长时,就可以求出的长.”
老师肯定了小慧同学结论的正确性.若 , , 请你帮小慧求出的长.
8. 学完勾股定理后,小宇碰到了一道题:如图1,在四边形ABCD中,AC⊥BD , 垂足为O , 若AB=5,CD=4,BC=6,则AD的长为 ▲ .他不会做,去问同桌小轩,小轩通过思考后,耐心地对小宇讲道:“因为AC⊥BD , 垂足为O , 那么在四边形ABCD中有四个直角三角形,利用勾股定理可得AD2=OA2+OD2 , BC2=OB2+OC2 , AB2=OA2+OB2 , CD2=OC2+OD2...”小轩话没讲完,小宇就讲道:“我知道了,原来AD2+BC2与AB2+CD2之间有某种数量关系.”并对小轩表示感谢.
 (1)、请你直接写出AD的长.(2)、如图2,分别在△ABC的边BC和边AB上向外作等腰Rt△BCQ和等腰Rt△ABP , 连接PC , PQ .
(1)、请你直接写出AD的长.(2)、如图2,分别在△ABC的边BC和边AB上向外作等腰Rt△BCQ和等腰Rt△ABP , 连接PC , PQ .①若AC=4,BC=8,连接AQ , 交PC于点D , 当∠ACB=90°时,求PQ的长;
②如图3,若AB=10,BC=8,PC= , 当∠ACB≠90°时,求△ABC的面积.
9. 我们定义:有一组邻边相等且有一组对角互补的凸四边形叫做等补四边形. (1)、如图1,是等边三角形,在上任取一点D(B、C除外),连接 , 我们把绕点A逆时针旋转60°,则与重合,点D的对应点E.请根据给出的定义判断,四边形(选择是或不是)等补四边形.(2)、如图2,等补四边形中, , , 若 , 求的长.(3)、如图3,四边形中, , , , 求四边形面积的最大值.10. 已知四边形ABCD中,E , F分别是AB , AD边上的点,DE与CF交于点G , 令=k .
(1)、如图1,是等边三角形,在上任取一点D(B、C除外),连接 , 我们把绕点A逆时针旋转60°,则与重合,点D的对应点E.请根据给出的定义判断,四边形(选择是或不是)等补四边形.(2)、如图2,等补四边形中, , , 若 , 求的长.(3)、如图3,四边形中, , , , 求四边形面积的最大值.10. 已知四边形ABCD中,E , F分别是AB , AD边上的点,DE与CF交于点G , 令=k .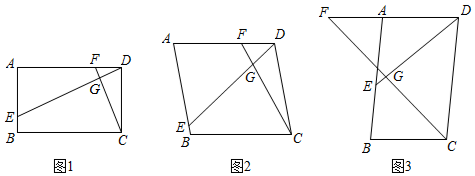 (1)、特例解析:如图1,若四边形ABCD是矩形,且DE⊥CF , 求证:=k;(2)、类比探究:如图2,若四边形ABCD是平行四边形,当∠B与∠EGC满足什么关系时,=k仍然成立?并证明你的结论;(3)、拓展延伸:如图3,在(2)的条件下, , ∠AED=45°,求DE的长.11. 通过对下面数学模型的研究学习,解决下列问题:.
(1)、特例解析:如图1,若四边形ABCD是矩形,且DE⊥CF , 求证:=k;(2)、类比探究:如图2,若四边形ABCD是平行四边形,当∠B与∠EGC满足什么关系时,=k仍然成立?并证明你的结论;(3)、拓展延伸:如图3,在(2)的条件下, , ∠AED=45°,求DE的长.11. 通过对下面数学模型的研究学习,解决下列问题:.
 (1)、【模型呈现】某兴趣小组在从汉代数学家赵爽的弦图(如图1,由外到内含三个正方形)中提炼出两个三角形全等模型图(如图2),即“一线三等角”模型和“K字”模型.
(1)、【模型呈现】某兴趣小组在从汉代数学家赵爽的弦图(如图1,由外到内含三个正方形)中提炼出两个三角形全等模型图(如图2),即“一线三等角”模型和“K字”模型.请在上图2中选择其中一个模型进行证明 .
(2)、【模型应用】如图3,正方形ABCD中,AE⊥DE,DE-4,求△CDE的面积.(3)、如图4,四边形ABCD中, , AB⊥BC,AD=2,BC=3, , DE=DC,求△ADE的面积.12. 综合与实践在一次综合实践活动课上,王老师给每位同学各发了一张正方形纸片,请同学们思考如何仅通过折纸的方法来确定正方形一边上的一个三等分点.


【操作探究】
“乘风”小组的同学经过一番思考和讨论交流后,进行了如下操作:
第1步:如图1所示,先将正方形纸片ABCD对折,使点A与点B重合,然后展开铺平,折痕为EF;
第2步:将BC边沿CE翻折到GC的位置;
第3步:延长EG交AD于点H,则点H为AD边的三等分点.
证明过程如下:连接CH,
∵正方形ABCD沿CE折叠,
∴∠D=∠B=∠CGH=90°, ① ,
又∵CH=CH
∴△CGH≌△CDH,
∴GH=DH.
由题意可知E是AB的中点,设AB=6(个单位),DH=x,则AE=BE=EG=3,
在Rt△AEH中,可列方程: ② , (方程不要求化简)解得:DH= ③ , 即H是AD边的三等分点.
“破浪”小组是这样操作的:
第1步:如图2所示,先将正方形纸片对折,使点A与点B重合,然后展开铺平,折痕为EF;
第2步:再将正方形纸片对折,使点B与点D重合,再展开铺平,折痕为AC,沿DE翻折得折痕DE交AC于点G;
第3步:过点G折叠正方形纸片ABCD,使折痕MNIIAD.
【过程思考】
(1)、“乘风”小组的证明过程中,三个空的所填的内容分别是: ① , ②: , ③: ;(2)、结合“破浪”小组操作过程,判断点M是否为AB边的三等分点,并证明你的结论;(3)、【拓展提升】如图3,在菱形ABCD中,AB=5,BD=6,E是BD上的一个三等分点,记点D关于AE的对称点为D',射线ED'与菱形ABCD 的边交于点F,请直接写出D'F的长.13. (1)、【问题情境】如图1,小明把三角板EFG()放置到矩形ABCD中,使得顶点E、F、G分别落在AD、CD、AB上,你发现线段ED与AG有什么数量关系?
(1)、【问题情境】如图1,小明把三角板EFG()放置到矩形ABCD中,使得顶点E、F、G分别落在AD、CD、AB上,你发现线段ED与AG有什么数量关系?直接写出结论:(不用证明).
(2)、【变式探究】如图2,小明把三角板EFG()放置到矩形ABCD中,使得顶点E、F、G分别在AD、BC、AB边上,若 , , 求BG的长.(3)、【拓展应用】如图3,小明把三角形EFG放置到平行四边形ABCD中,使得顶点E、F、G分别落在AD、BC、AB边上,若 , , , 求出的值.14. (1)、【观察与猜想】
(1)、【观察与猜想】如图1,点是矩形内一点,过点的直线 , 分别交矩形的边为点 . 若 , 则;
(2)、【类比探究】如图2,在平行四边形中,点分别在边上,连接与交于点 . 求证:;
(3)、【拓展延伸】如图3,在四边形中, , 在边上,连接与交于点 , 当时,求的值.
15. (1)、【知识呈现】如图①,已知矩形ABCD的对角线AC的垂直平分线与边AD、BC分别交于点E、F.求证:四边形AFCE是菱形;(2)、【知识应用】如图②,直线EF分别交矩形ABCD的边AD、BC于点E、F , 将矩形ABCD沿EF翻折,使点C的对称点与点A重合,点D的对称点为G , 若 , , 则EF的长为;(3)、【知识拓展】如图③,直线EF分别交平行四边形ABCD的边AD、BC于点E、F , 将平行四边形ABCD沿EF翻折,使点C的对称点与点A重合,点D的对称点为G , 若 , , , 则四边形AFCE的面积为.16.
(1)、【知识呈现】如图①,已知矩形ABCD的对角线AC的垂直平分线与边AD、BC分别交于点E、F.求证:四边形AFCE是菱形;(2)、【知识应用】如图②,直线EF分别交矩形ABCD的边AD、BC于点E、F , 将矩形ABCD沿EF翻折,使点C的对称点与点A重合,点D的对称点为G , 若 , , 则EF的长为;(3)、【知识拓展】如图③,直线EF分别交平行四边形ABCD的边AD、BC于点E、F , 将平行四边形ABCD沿EF翻折,使点C的对称点与点A重合,点D的对称点为G , 若 , , , 则四边形AFCE的面积为.16.[温故知新]
在证明“三角形的中位线平行于第三边,且等于第三边的一半”时,小明结合图1给出如下证明思路:作CF∥AD交DE的延长线于点F,再证△ADE≌△CFE,再证四边形DBCF是平行四边形,即可证明定理.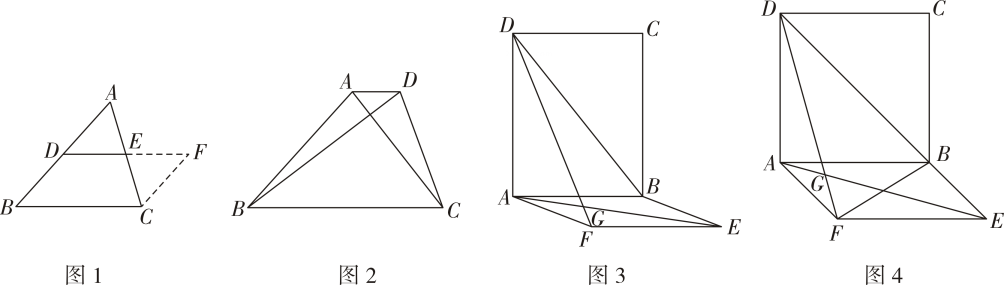 (1)、[新知体验]
(1)、[新知体验]小明思考后发现:作平行线可以构成全等三角形或平行四边形,以达到解决问题的目的.如图2,在四边形ABCD中,AD∥BC,AC⊥BD,若AC=3,BD=4,AD=1,则BC的值为
(2)、[灵活运用]如图3,在矩形ABCD和ABEF中,连接DF、AE交于点G,连接DB.若AE=DF=DB,求∠FGE的度数;
(3)、[拓展延伸]如图4在第(2)题的条件下,连接BF,若AB=4D= , 求△BEF的面积.
17. (1)、【探究证明】某班数学课题学习小组对矩形内两条互相垂直的线段与矩形两邻边的数量关系进行探究,提出下列问题,请你给出证明:
(1)、【探究证明】某班数学课题学习小组对矩形内两条互相垂直的线段与矩形两邻边的数量关系进行探究,提出下列问题,请你给出证明:如图①,在矩形中, , 分别交于点E、F,分别交于点G、H,求证:;
(2)、【结论应用】如图②,将矩形沿折叠,使得点B和点D重合,若 , 求折痕的长;(3)、【拓展运用】如图③,将矩形沿折叠.使得点D落在边上的点G处,点C落在点P处,得到四边形 , 若 , 求的长.18. (1)、【探究发现】
(1)、【探究发现】如图1,正方形ABCD的对角线交于点O , E是AD边上一点,作OF⊥OE交AB于点F . 学习小队发现,不论点E在AD边上运动过程中,△AOE与△BOF恒全等.请你证明这个结论;
(2)、【类比迁移】如图2,矩形ABCD的对角线交于点O , ∠ABD=30°,E是BA延长线上一点,将OE绕点O逆时针旋转60°得到OF , 点F恰好落在DA的延长线上,求的值;
(3)、【拓展提升】如图3,等腰△ABC中,AB=AC , ∠BAC=120°,BC=12,点E是BC边上一点,以BE为边在BC的上方作等边△BEF , 连接CF , 取CF的中点M , 连接AM , 当AM=时,直接写出BE的长.
19. 在正方形中,、分别为边上的两点,连接、并延长交于点 , 连接 , 为上一点,连接、 . (1)、如图 , 若为的中点,且 , , 求线段的长;(2)、如图 , 过点作 , 且 , 连接 , 刚好交的中点 , 当时,求证:;(3)、如图 , 在的条件下,点为线段上一动点,连接 , 作于点 , 将沿翻折得到 , 点、分别为线段、上两点,且 , , 连接、交于点 , 连接 , 请直接写出面积的最大值.20. 在正方形 中,等腰直角 , ,连接 ,H为 中点,连接 、 、 ,发现 和 为定值.
(1)、如图 , 若为的中点,且 , , 求线段的长;(2)、如图 , 过点作 , 且 , 连接 , 刚好交的中点 , 当时,求证:;(3)、如图 , 在的条件下,点为线段上一动点,连接 , 作于点 , 将沿翻折得到 , 点、分别为线段、上两点,且 , , 连接、交于点 , 连接 , 请直接写出面积的最大值.20. 在正方形 中,等腰直角 , ,连接 ,H为 中点,连接 、 、 ,发现 和 为定值.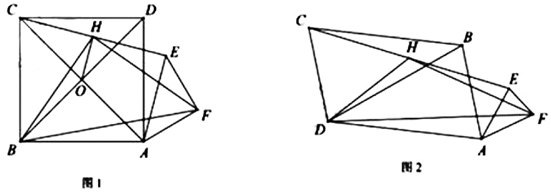 (1)、① ▲ ;
(1)、① ▲ ;② ▲ .
③小明为了证明①②,连接 交 于O , 连接 ,证明了 和 的关系,请你按他的思路证明①②.
(2)、小明又用三个相似三角形(两个大三角形全等)摆出如图2, , ( )求① (用k的代数式表示)
② (用k、 的代数式表示)
21. 在矩形中,点是射线上一动点,连接 , 过点作于点 , 交直线于点 . (1)、当矩形是正方形时,以点为直角顶点在正方形的外部作等腰直角三角形 , 连接 .
(1)、当矩形是正方形时,以点为直角顶点在正方形的外部作等腰直角三角形 , 连接 .①如图1,若点在线段上,则线段与之间的数量关系是 ▲ , 位置关系是 ▲ ;
②如图2,若点在线段的延长线上,①中的结论还成立吗?如果成立,请给予证明;如果不成立,请说明理由;
(2)、如图3,若点在线段上,以和为邻边作平行四边形 , 是中点,连接 , , , 求的最小值.22. 已知矩形 , 点E、F分别在、边上运动,连接、 , 记、交于点P .-
 (1)、如图1,若 , , , 求线段的长度;(2)、如图2,若 , , 求;(3)、如图3,连接 , 若 , , , 求的长度.23. 在菱形和菱形中, .
(1)、如图1,若 , , , 求线段的长度;(2)、如图2,若 , , 求;(3)、如图3,连接 , 若 , , , 求的长度.23. 在菱形和菱形中, . (1)、如图1,若点分别在边上,点F在菱形内部,连接 , 直接写出的长度为;(2)、如图2,把菱形绕点B顺时针旋转 , 连接 , 判断与的数量关系,并给出证明;(3)、如图3,①把菱形继续绕点B顺时针旋转,连接为的中点,连接 , 试探究与的关系;②直接写出菱形绕B点旋转过程中的取值范围.24. 已知 , AB=AC , AB>BC .
(1)、如图1,若点分别在边上,点F在菱形内部,连接 , 直接写出的长度为;(2)、如图2,把菱形绕点B顺时针旋转 , 连接 , 判断与的数量关系,并给出证明;(3)、如图3,①把菱形继续绕点B顺时针旋转,连接为的中点,连接 , 试探究与的关系;②直接写出菱形绕B点旋转过程中的取值范围.24. 已知 , AB=AC , AB>BC .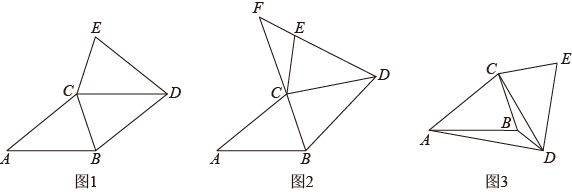 (1)、如图1,CB平分∠ACD , 求证:四边形ABDC是菱形;(2)、如图2,将(1)中的△CDE绕点C逆时针旋转(旋转角小于∠BAC),BC , DE的延长线相交于点F , 用等式表示∠ACE与∠EFC之间的数量关系,并证明;(3)、如图3,将(1)中的△CDE绕点C顺时针旋转(旋转角小于∠ABC),若 , 求∠ADB的度数.
(1)、如图1,CB平分∠ACD , 求证:四边形ABDC是菱形;(2)、如图2,将(1)中的△CDE绕点C逆时针旋转(旋转角小于∠BAC),BC , DE的延长线相交于点F , 用等式表示∠ACE与∠EFC之间的数量关系,并证明;(3)、如图3,将(1)中的△CDE绕点C顺时针旋转(旋转角小于∠ABC),若 , 求∠ADB的度数.