2024年中考数学精选压轴题之圆(二)
试卷更新日期:2024-05-12 类型:三轮冲刺
一、实践探究题
-
1. 已知点 , , , 是上的四个点,且弦 , 于点.
 (1)、如图1,点是的中点,在探究 , , 之间的数量关系时,圆圆同学提出解决的思路:在上截取 , 连结 , 可以通过证明三角形全等,从而得到有关线段的等量关系.请你帮圆圆同学写出完整的探究过程.(2)、如图2,是等边三角形,若 , , 利用(1)的结论,求的周长.(3)、如图3,若 , , , , 连结 , 求的度数.2. 综合探究
(1)、如图1,点是的中点,在探究 , , 之间的数量关系时,圆圆同学提出解决的思路:在上截取 , 连结 , 可以通过证明三角形全等,从而得到有关线段的等量关系.请你帮圆圆同学写出完整的探究过程.(2)、如图2,是等边三角形,若 , , 利用(1)的结论,求的周长.(3)、如图3,若 , , , , 连结 , 求的度数.2. 综合探究如图1,是的内接三角形,是上的一点,连接交于点 , 点在上,满足 , 交于点 , , 连接 .
 (1)、求证: .(2)、求证: .(3)、如图2,为的直径,设 , 当的长为2时,求的长.3. 【定义新知】
(1)、求证: .(2)、求证: .(3)、如图2,为的直径,设 , 当的长为2时,求的长.3. 【定义新知】如图1,是上两点,且在直径的上方,若直径上存在一点 , 连接 , 满足 , 则称是的“幸运角”.
 (1)、【问题探究】如图2,是的直径,弦是上的一点,连接交于点 , 连接 .
(1)、【问题探究】如图2,是的直径,弦是上的一点,连接交于点 , 连接 .①是的“幸运角”吗?请说明理由;
②设所对的圆心角为 , 请用含的式子表示的“幸运角”的度数;
(2)、【拓展延伸】如图3,在(1)的条件下,若直径 , 的“幸运角”为 , , 求的长.4. 综合与实践数学活动课上,老师出示了一个问题:如图,已知三只蚂蚁A、、在半径为的上静止不动,第四只蚂蚁在上的移动,并始终保持 .
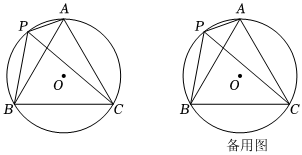 (1)、请判断的形状;“数学希望小组”很快得出结论,请你回答这个结论:是三角形;(2)、“数学智慧小组”继续研究发现:当第四只蚂蚁在上的移动时,线段、、三者之间存在一种数量关系:请你写出这种数量关系: ▲ , 并加以证明;(3)、“数学攀峰小组”突发奇想,深入探究发现:若第五只蚂蚁同时随着蚂蚁的移动而移动,且始终位于线段的中点,在这个运动过程中,线段的长度一定存在最小值,请你求出线段的最小值是(不写解答过程,直接写出结果).5. 如图
(1)、请判断的形状;“数学希望小组”很快得出结论,请你回答这个结论:是三角形;(2)、“数学智慧小组”继续研究发现:当第四只蚂蚁在上的移动时,线段、、三者之间存在一种数量关系:请你写出这种数量关系: ▲ , 并加以证明;(3)、“数学攀峰小组”突发奇想,深入探究发现:若第五只蚂蚁同时随着蚂蚁的移动而移动,且始终位于线段的中点,在这个运动过程中,线段的长度一定存在最小值,请你求出线段的最小值是(不写解答过程,直接写出结果).5. 如图 (1)、课本再现:如图1, 是的一个外角,写出与 , 的数量关系(2)、类比探究:如图2,是与的公共边, , .
(1)、课本再现:如图1, 是的一个外角,写出与 , 的数量关系(2)、类比探究:如图2,是与的公共边, , .①与的数量关系是 ▲ ;
②求证
(3)、拓展应用:如图3,点D是正方形内一点,且在以O 为圆心, 为半径的圆弧上,若 , , 直接写出线段的长.6. 如图1,扇形AOB中,∠AOB=90°,OA=6,点P在半径OB上,连接AP . (1)、把△AOP沿AP翻折,点O的对称点为点Q .
(1)、把△AOP沿AP翻折,点O的对称点为点Q .①当点Q刚好落在弧AB上,求弧AQ的长;
②如图2,点Q落在扇形AOB外,AQ与弧AB交于点C , 过点Q作QH⊥OA , 垂足为H ,
探究OH、AH、QC之间的数量关系,并说明理由;
(2)、如图3,记扇形AOB在直线AP上方的部分为图形W , 把图形W沿着AP翻折,点B的对称点为点E , 弧AE与OA交于点F , 若OF=2,求PO的长.7. 【我们画不出一个完美的圆,但完美的圆是存在的,虽不能至,心向往之罗翔】已知四边形是半径为的内接四边形,弦的长度是 , 点是劣弧上的一个动点.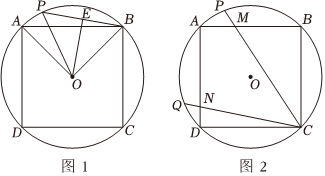 (1)、填空:的度数是 ,并判断平行四边形是否会是正方形 填“是”或“不是”;(2)、如图 , 若点是弦的中点,连接 , , 当点沿着劣弧从点开始,顺时针运动到点时,求的外心所经过的路径的长度;(3)、如图 , 点是劣弧另一个动点,并始终满足 , 、分别交弦 , 于点、 , 连接记的面积为 , 的面积为 , 的面积为 .
(1)、填空:的度数是 ,并判断平行四边形是否会是正方形 填“是”或“不是”;(2)、如图 , 若点是弦的中点,连接 , , 当点沿着劣弧从点开始,顺时针运动到点时,求的外心所经过的路径的长度;(3)、如图 , 点是劣弧另一个动点,并始终满足 , 、分别交弦 , 于点、 , 连接记的面积为 , 的面积为 , 的面积为 .直接写出 , , 之间的数量关系;不必进行证明
令 , , 若满足 , 求 , 的值.
8. 小辉同学观看2022卡塔尔世界杯时发现,优秀的球员通常都能选择最优的点射门(仅从射门角度大小考虑).这引起了小辉同学的兴趣,于是他展开了一次有趣的数学探究.
【提出问题】如图所示.球员带球沿直线奔向球门 ,
探究:是否存在一个位置,使得射门角度最大.
【分析问题】因为线段长度不变,我们联想到圆中的弦和圆周角.
如图1,射线与相交,点M,点A,点N分别在圆外、圆上、圆内,连接 .
【解决问题】
 (1)、如图1,比较的大小:(用“<”连接起来).(2)、如图2,点A是射线上一动点(点A不与点B重合).证明:当的外接圆与射线相切时,最大.(3)、【延伸拓展】在(2)的条件下,如果 . 当最大时.证明: .9.
(1)、如图1,比较的大小:(用“<”连接起来).(2)、如图2,点A是射线上一动点(点A不与点B重合).证明:当的外接圆与射线相切时,最大.(3)、【延伸拓展】在(2)的条件下,如果 . 当最大时.证明: .9. (1)、【证明体验】
(1)、【证明体验】如图1,⊙O是等腰△ABC的外接圆,AB=AC , 在上取一点P , 连结AP , BP , CP . 求证:∠APB=∠PAC+∠PCA;
(2)、【思考探究】如图2,在(1)条件下,若点P为的中点,AB=6,PB=5,求PA的值;
(3)、【拓展延伸】如图3,⊙O的半径为5,弦BC=6,弦CP=5,延长AP交BC的延长线于点E , 且∠ABP=∠E , 求AP•PE的值.
10. 如图1, 中, 边上的中线 ,延长 交 的外接圆于点 ,过点 作DE BC交圆于点 ,延长 交 的延长线于点 ,连结 . (1)、【特殊尝试】若 , ,求 和 的长;(2)、【规律探索】
(1)、【特殊尝试】若 , ,求 和 的长;(2)、【规律探索】①求证: ;
②设 , ,求 关于 的函数表达式:
(3)、【拓展应用】如图2,作 交线段 于 ,连结 ,当 的面积是 面积的6倍时,求 的值.
11. 阅读资料:如图1,在平面之间坐标系中, , 两点的坐标分别为 , , 由勾股定理得 , 所以 , 两点间的距离为 . 我们知道,圆可以看成到圆心距离等于半径的点的集合,如图2,在平面直角坐标系中,为圆上任意一点,则到原点的距离的平方为 , 当的半径为时,的方程可写为: .问题拓展:如果圆心坐标为 , 半径为 , 那么的方程可以写为 .
综合应用:如图3,与轴相切于原点 , 点坐标为 , 是上一点,连接 , 使 , 作 , 垂足为 , 延长交轴于点 , 连接 .
 (1)、求证是的切线;(2)、是否存在到四点 , , , 距离都相等的点?若存在,求点坐标,并写出以为圆心,以为半径的的方程;若不存在,说明理由.12. 阅读材料,某个学习小组成员发现:在等腰中,AD平分 , ∵ , , ∴ , 他们猜想:在任意中,一个内角角平分线分对边所成的两条线段与这个内角的两边对应成比例.
(1)、求证是的切线;(2)、是否存在到四点 , , , 距离都相等的点?若存在,求点坐标,并写出以为圆心,以为半径的的方程;若不存在,说明理由.12. 阅读材料,某个学习小组成员发现:在等腰中,AD平分 , ∵ , , ∴ , 他们猜想:在任意中,一个内角角平分线分对边所成的两条线段与这个内角的两边对应成比例.
【证明猜想】如图1所示,在中,AD平分 , 求证:.
丹丹认为,可以通过构造相似三角形的方法来证明;
思思认为,可以通过比较和面积的角度来证明.
(1)、请你从上面的方法中选择一种进行证明.(2)、【尝试应用】如图2,是的外接圆,点E是上一点(与B不重合,且 , 连结 , 并延长AE,BC交于点D,H为AE的中点,连结BH交AC于点G,求的值.(3)、【拓展提高】如图3,在(2)的条件下,延长交于点F,若 , , 求的直径(用x的代数式表示).二、综合题
-
13. 如图1,直线与轴交于点 , 与轴交于点 , 点是线段上一动点.以点为圆心,长为半径作交轴于另一点 , 交直线于点和点 , 连接并延长交于点.

 (1)、如图1, , ;(2)、如图2,连接 , 当时,求证:;(3)、当点在线段上运动时,求的最大值.14. 如图1,E点为x轴正半轴上一点,交x轴于A、B两点,交y轴于C、D两点,P点为劣弧上一个动点,且、 .
(1)、如图1, , ;(2)、如图2,连接 , 当时,求证:;(3)、当点在线段上运动时,求的最大值.14. 如图1,E点为x轴正半轴上一点,交x轴于A、B两点,交y轴于C、D两点,P点为劣弧上一个动点,且、 . (1)、的度数为;(2)、如图2,连结 , 取中点G,连结 , 则的最大值为;(3)、如图3,连接、、、 . 若平分交于Q点,求的长;(4)、如图4,连接、 , 当P点运动时(不与B、C两点重合),求证:为定值,并求出这个定值.15. 如图1,内接于 , 为直径,点D为上一点,连接交于点G,于点F交于点E.
(1)、的度数为;(2)、如图2,连结 , 取中点G,连结 , 则的最大值为;(3)、如图3,连接、、、 . 若平分交于Q点,求的长;(4)、如图4,连接、 , 当P点运动时(不与B、C两点重合),求证:为定值,并求出这个定值.15. 如图1,内接于 , 为直径,点D为上一点,连接交于点G,于点F交于点E.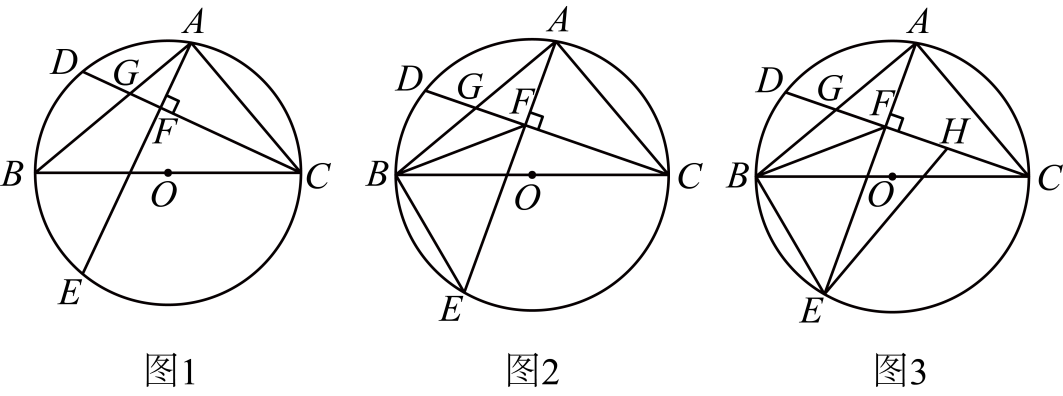 (1)、求证:;(2)、如图2,连接 , 若 , 求证:;(3)、在(2)的条件下,如图3,点H是上一点,连接 , , 若 , 求线段的长.16. 如图1,四边形内接于 , 为直径,上存在点 , 满足 , 连接并延长交的延长线于点 , 与交于点 .
(1)、求证:;(2)、如图2,连接 , 若 , 求证:;(3)、在(2)的条件下,如图3,点H是上一点,连接 , , 若 , 求线段的长.16. 如图1,四边形内接于 , 为直径,上存在点 , 满足 , 连接并延长交的延长线于点 , 与交于点 . (1)、若 , 请用含的代数式表示;(2)、如图2,连接 , . 求证:;(3)、如图3,在(2)的条件下,连接 , , 求的最小值.17. 如图1,C,D是半圆ACB上的两点,若直径AB上存在一点P,确足∠APC=∠BPD,则称∠CPD是的“美丽角”.
(1)、若 , 请用含的代数式表示;(2)、如图2,连接 , . 求证:;(3)、如图3,在(2)的条件下,连接 , , 求的最小值.17. 如图1,C,D是半圆ACB上的两点,若直径AB上存在一点P,确足∠APC=∠BPD,则称∠CPD是的“美丽角”. (1)、如图2,AB是⊙O的直径,弦CE⊥AB,D是上一点,连结ED交AB于点P,连结CP,∠CPD是的“美丽角”吗?请说明理由;(2)、设的度数为α,请用含α的式子表示的“美丽角”度数;(3)、如图3,在(1)的条件下,若直径AB=5,的“美丽角”为90°,当时,求CE的长.18. 如图,△ABC内接于⊙O , 弦CD、BE相交于点F , ∠DFB﹣∠EDC=90﹣∠ACD .
(1)、如图2,AB是⊙O的直径,弦CE⊥AB,D是上一点,连结ED交AB于点P,连结CP,∠CPD是的“美丽角”吗?请说明理由;(2)、设的度数为α,请用含α的式子表示的“美丽角”度数;(3)、如图3,在(1)的条件下,若直径AB=5,的“美丽角”为90°,当时,求CE的长.18. 如图,△ABC内接于⊙O , 弦CD、BE相交于点F , ∠DFB﹣∠EDC=90﹣∠ACD . (1)、如图1,求证:AB为⊙O的直径;(2)、如图2,过点D作DG∥BE , 求证:=;(3)、如图3,在(2)的条件下,CD与AB相交于点H , 连接GH并延长交⊙O于点K , 连接DK , 沿DK所在直线作劣弧DK的轴对称图形经过点H , DG=5,AC=8,求线段DE的长.19. 已知:的两条弦 , 相交于点M,且.
(1)、如图1,求证:AB为⊙O的直径;(2)、如图2,过点D作DG∥BE , 求证:=;(3)、如图3,在(2)的条件下,CD与AB相交于点H , 连接GH并延长交⊙O于点K , 连接DK , 沿DK所在直线作劣弧DK的轴对称图形经过点H , DG=5,AC=8,求线段DE的长.19. 已知:的两条弦 , 相交于点M,且. (1)、如图1,连接.求证:.(2)、如图2,若 , 点E为弧上一点, , 交于点F,连接、.
(1)、如图1,连接.求证:.(2)、如图2,若 , 点E为弧上一点, , 交于点F,连接、.①求的度数(用含的代数式表示).
②若 , , 求的面积.
20. 如图1,AC为▱ABCD的对角线,△ABC的外接圆⊙O交CD于点E (1)、求证:∠BAC=∠ABE;(2)、如图2,当AB=AC时,连接OA、OB , 求证△GOB∽△GBA;(3)、如图3,在(2)的条件下,记AC、BE的交点为点F,当时,求sin∠EAG的值.
(1)、求证:∠BAC=∠ABE;(2)、如图2,当AB=AC时,连接OA、OB , 求证△GOB∽△GBA;(3)、如图3,在(2)的条件下,记AC、BE的交点为点F,当时,求sin∠EAG的值.
21. 已知内接于 , 点F是弧AC的中点,连接OF交AC于点H . (1)、如图1,求证:;(2)、如图2,AD是的高,延长AD交于点K , 若 , 求证:;(3)、如图3,在(2)的条件下,延长FO交BD于点E , 连接EK , 点M在CH上,连接OM . 若 , 求HF的长.22. 在中,弦交于点 , 连接于点.
(1)、如图1,求证:;(2)、如图2,AD是的高,延长AD交于点K , 若 , 求证:;(3)、如图3,在(2)的条件下,延长FO交BD于点E , 连接EK , 点M在CH上,连接OM . 若 , 求HF的长.22. 在中,弦交于点 , 连接于点. (1)、求证:;(2)、为弦BC中点,过点作 , 连接HF,并延长HF交AC于 , 求证:;(3)、在(2 )的条件下,若 , 求的直径。23. 已知点 , 过点作轴于点 , 伷于点 , 以为圆心,长为半径作圆交于点 , 连接并延长交于点 .
(1)、求证:;(2)、为弦BC中点,过点作 , 连接HF,并延长HF交AC于 , 求证:;(3)、在(2 )的条件下,若 , 求的直径。23. 已知点 , 过点作轴于点 , 伷于点 , 以为圆心,长为半径作圆交于点 , 连接并延长交于点 .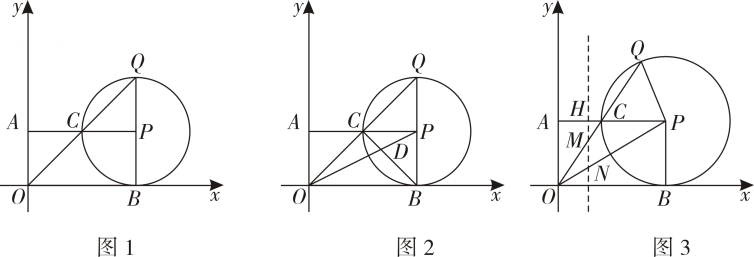 (1)、当点、、在同一条直线上时.
(1)、当点、、在同一条直线上时.①如图1,点是否为线段的中点?若是,请证明:若不是,请说明理由.
②如图2,连接、 , 两线交于点 , 当 , 时,求的长;
(2)、如图3,点为线段上一动点,过点作轴的平行线,分别交、于点、 . 若(为定值),试探究在点运动的过程中,的值是否为定值?如果是,请求出这个定值(用含的代数式表示);如果不是,请说明理由.24. 如图,已知是的直径, , 切于点 , 过点作交于点 , 若 . (1)、如图1,连接 , 求证:;(2)、如图2,是上一点,在上取一点 , 使 , 连接 . 请问:三条线段有怎样的数量关系?并证明你的结论.
(1)、如图1,连接 , 求证:;(2)、如图2,是上一点,在上取一点 , 使 , 连接 . 请问:三条线段有怎样的数量关系?并证明你的结论.