(通用版)2024年中考数学重点知识冲刺训练---代数式
试卷更新日期:2024-05-10 类型:三轮冲刺
一、选择题
-
1. 据国家医保局最新消息,全国统一的医保信息平台已全面建成,在全国31个省份和新疆生产建设兵团全域上线,为1360 000 000参保人提供医保服务,医保信息化标准化取得里程碑式突破.数1360 000 000用科学记数法表示为( )A、1.36×107 B、13.6×108 C、1.36×109 D、0.136×10102. 计算 的结果是( )A、 B、 C、1 D、3. 某种商品m千克的售价为n元,那么这种商品8千克的售价为( )A、 (元) B、 (元) C、 (元) D、 (元)4. 若分式的值为0,则x的值为( )A、-3 B、-2 C、0 D、25. 计算的结果为( )A、 B、 C、 D、6. 关于x,y的方程组的解满足 , 则的值是( )A、1 B、2 C、4 D、87. 在函数y=中,自变量x的取值范围是( )A、x≥3 B、x≥﹣3 C、x≥3且x≠0 D、x≥﹣3且x≠08. 已知 , 则与最接近的整数为( )A、2 B、3 C、4 D、59. 下面的计算过程中,从哪一步开始出现错误( ).
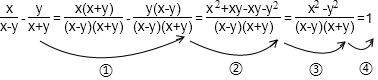 A、① B、② C、③ D、④10. 我们将如图所示的两种排列形式的点的个数分别称作“三角形数”(如1,3,6,10,⋯)和“四边形数”(如1,4,9,16,…),在小于200的数中,设最大的“三角形数”为a,最大的“四边形数”为b,则a+b的值为( )
A、① B、② C、③ D、④10. 我们将如图所示的两种排列形式的点的个数分别称作“三角形数”(如1,3,6,10,⋯)和“四边形数”(如1,4,9,16,…),在小于200的数中,设最大的“三角形数”为a,最大的“四边形数”为b,则a+b的值为( ) A、33 B、301 C、386 D、571
A、33 B、301 C、386 D、571二、填空题
-
11. 计算的结果是.12. 若式子在实数范围内有意义,则x的取值范围是 .13. 已知x,y为实数,且满足 , 记的最大值为M,最小值为m,则M+m=.14. 人们把 这个数叫做黄金比,著名数学家华罗庚优选法中的“0.618法”就应用了黄金比.设 , ,记 , ,…, ,则 .
三、解答题
-
15. 先化简,再求值: , 从 , , , , 中取一个合适的数作为的值代入求值.16. 计算:17. 请先将下式化简,再选择一个使原式有意义的数代入求值.
( ﹣1)÷ .
18. 已知求的值。19. 已知与(为常数)成正比例,且当时, , 当时,.(1)、求关于的函数表达式.(2)、若点在(1)中函数的图象上,求的值.20. 我们知道,任意一个正整数n都可以进行这样的分解:n=p×q(p,q是正整数,且p≤q),在n的所有这种分解中,如果p,q两因数之差的绝对值最小,我们就称p×q是n的最佳分解.并规定:F(n)= .例如12可以分解成1×12,2×6或3×4,因为12﹣1>6﹣2>4﹣3,所以3×4是12的最佳分解,所以F(12)= .
(Ⅰ)如果一个正整数m是另外一个正整数n的平方,我们称正整数m是完全平方数.
求证:对任意一个完全平方数m,总有F(m)=1;
(Ⅱ)如果一个两位正整数t,t=10x+y(1≤x≤y≤9,x,y为自然数),交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为36,那么我们称这个数t为“吉祥数”,求所有“吉祥数”;
(Ⅲ)在(2)所得“吉祥数”中,求F(t)的最大值.
四、综合题
-
21. 如图是2019年1月份的日历.任意选择图中的菱形框部分,将每个菱形框部分中去掉中间位置的数之后,相对的两对数分别相乘,再相减,例如:9×11-3×17=48,13×15-7×21=48.不难发现,结果都是48
 (1)、请证明发现的规律;(2)、小明说:他用一个如图所示菱形框,框出5个数字,其中最小数与最大数的积是120,请判断他的说法是否符合题意.22. 如图1,将长为2a+3,宽为2a的矩形分割成四个全等的直角三角形,拼成“赵爽弦图”(如图2),得到大小两个正方形,
(1)、请证明发现的规律;(2)、小明说:他用一个如图所示菱形框,框出5个数字,其中最小数与最大数的积是120,请判断他的说法是否符合题意.22. 如图1,将长为2a+3,宽为2a的矩形分割成四个全等的直角三角形,拼成“赵爽弦图”(如图2),得到大小两个正方形,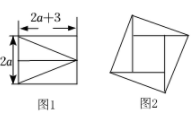 (1)、用关于a的代数式表示图2中小正方形的边长(2)、当a=3时,该小正方形的面积是多少?23. 在平面直角坐标系中,给出如下定义:为图形上任意一点,如果点到直线的距离等于图形上任意两点距离的最大值时,那么点称为直线的“伴随点”.
(1)、用关于a的代数式表示图2中小正方形的边长(2)、当a=3时,该小正方形的面积是多少?23. 在平面直角坐标系中,给出如下定义:为图形上任意一点,如果点到直线的距离等于图形上任意两点距离的最大值时,那么点称为直线的“伴随点”.例如:如图1,已知点 , , 在线段上,则点是直线:轴的“伴随点”.
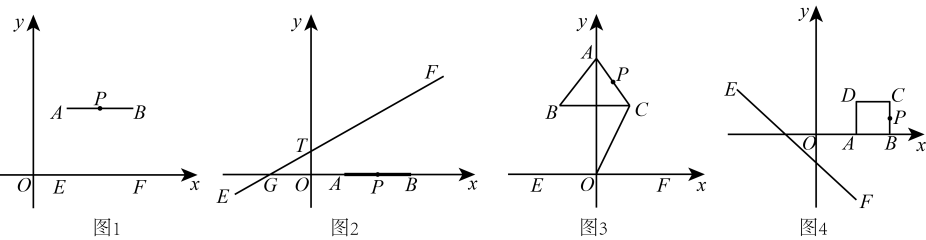 (1)、如图2,已知点 , , 是线段上一点,直线过 , 两点,当点是直线的“伴随点”时,求点的坐标;(2)、如图3,轴上方有一等边三角形 , 轴,顶点在轴上且在上方, , 点是上一点,且点是直线:轴的伴随点 . 当点到轴的距离最小时,求等边三角形的边长;(3)、如图4,以 , , 为顶点的正方形上始终存在点 , 使得点是直线:的伴随点 . 请直接写出的取值范围.
(1)、如图2,已知点 , , 是线段上一点,直线过 , 两点,当点是直线的“伴随点”时,求点的坐标;(2)、如图3,轴上方有一等边三角形 , 轴,顶点在轴上且在上方, , 点是上一点,且点是直线:轴的伴随点 . 当点到轴的距离最小时,求等边三角形的边长;(3)、如图4,以 , , 为顶点的正方形上始终存在点 , 使得点是直线:的伴随点 . 请直接写出的取值范围.