（通用版）2024年中考数学重点知识冲刺训练---有理数、实数

试卷更新日期：2024-05-10 类型：三轮冲刺

进入出卷网下载

一、选择题

1. 2022的相反数是（）

A、2022 B、 $- 2022$ C、 $\frac{1}{2022}$ D、 $- \frac{1}{2022}$

查看试题解析
2. 下列各数中，正整数是（）

A、3 B、2.1 C、0 D、-2

查看试题解析
3. 我国古代数学名著《九章算术》中对正负数的概念注有“今两算得失相反，要令正负以名之”、如：粮库把运进30吨粮食记为“ $+ 30$ ”，则“ $- 30$ ”表示（）

A、运出30吨粮食 B、亏损30吨粮食 C、卖掉30吨粮食 D、吃掉30吨粮食

查看试题解析
4. 下列二次根式中，与 $\sqrt{2}$ 是同类二次根式的是（）

A、 $\sqrt{4}$ B、 $\sqrt{6}$ C、 $\sqrt{8}$ D、 $\sqrt{12}$

查看试题解析
5. 面积为9的正方形，其边长等于（）

A、9的平方根 B、9的算术平方根 C、9的立方根 D、 $\sqrt{9}$ 的算术平方根

查看试题解析
6. 我们可用数轴直观研究有理数及其运算.如图，将物体从点A向左平移5个单位到点B，可以描述这一变化过程的算式为（）.

A、 $2 + (- 5)$ B、 $2 - (- 5)$ C、 $2 \times (- 5)$ D、 $2 \div (- 5)$

查看试题解析
7. 我国的珠穆朗玛峰高于海平面 $8848.86 m$ ，可记为 $+ 8848.86 m$ ，吐鲁番盆地大部分地面低于海平面 $500 m$ ，应记为（）

A、 $500 m$ B、 $- 500 m$ C、 $8348.86 m$ D、 $- 8348.86 m$

查看试题解析
8. 对于二次根式的乘法运算，一般地，有 $\sqrt{a} \cdot \sqrt{b} = \sqrt{a b}$ ．该运算法则成立的条件是（）

A、 $a > 0 ， b > 0$ B、 $a < 0 ， b < 0$ C、 $a \leq 0 ， b \leq 0$ D、 $a \geq 0 ， b \geq 0$

查看试题解析
9. 要使 $\sqrt{x - 2}$ 有意义，则 $x$ 的值可以是（）

A、0 B、-1 C、-2 D、2

查看试题解析
10. 定义一种新运算： $a * b = a^{2} - 3 b$ ，如 $2 * 1 = 2^{2} - 3 \times 1 = 1$ ，则 $(3 * 2) * (- 1)$ 的结果为（）

A、 $6$ B、 $12$ C、 $- 12$ D、 $- 6$

查看试题解析

二、填空题

11. 若式子 $\frac{\sqrt{x + 1}}{x - 2}$ 在实数范围内有意义，则x的取值范围是．

查看试题解析
12. 计算 $\sqrt{{(- 2)}^{2}}$ 的结果是.

查看试题解析
13. 若a，b互为相反数，c为8的立方根，则2a＋2b-c=.

查看试题解析
14. 已知点A（﹣2，b）与点B（a，3）关于原点对称，则a﹣b =.

查看试题解析

三、解答题

15. 计算 $| \sqrt{2} - 2 | - 2 \cos 45^{\circ} + {(- 1)}^{- 2} + \sqrt{8}$ ．

查看试题解析
16. 如图，点 $A$ 、 $B$ 在数轴上，它们对应的数分别为 $- 2$ ， $\frac{x}{x + 1}$ ，且点 $A$ 、 $B$ 到原点的距离相等.求 $x$ 的值.

查看试题解析
17. 我国南宋著名数学家秦九韶在他的著作《数书九章》一书中，给出了著名的秦九韶公式，也叫三斜求积公式，即若一个三角形的三边长分别为 $a$ ， $b$ ， $c$ ，则该三角形的面积 $S$ 满足公式：
$S = \sqrt{\frac{1}{4} [a^{2} b^{2} - {(\frac{a^{2} + b^{2} - c^{2}}{2})}^{2}]}$ .
现已知△ABC的三边长分别为1，3， $\sqrt{5}$ ，求△ABC的面积.

查看试题解析
18. 在5张相同的小纸条上，分别写有：① $\sqrt{2}$ ；② $\sqrt{8}$ ；③1；④乘法；⑤加法．将这5张小纸条做成5支签，①、②、③放在不透明的盒子A中搅匀，④、⑤放在不透明的盒子B中搅匀．

(1)、从盒子 $A$ 中任意抽出 $1$ 支签，抽到无理数的概率是；

(2)、先从盒子 $A$ 中任意抽出 $2$ 支签，再从盒子 $B$ 中任意抽出 $1$ 支签，求抽到的 $2$ 个实数进行相应的运算后结果是无理数的概率．

查看试题解析
19. 如图，小明在研究性学习活动中，对自己家所在的小区进行调查后发现，小区汽车入口宽AB为3.2m，在入口的一侧安装了停止杆CD，其中AE为支架．当停止杆仰起并与地面成60°角时，停止杆的端点C恰好与地面接触．此时CA为0.7m．在此状态下，若一辆货车高3m，宽2.5m，入口两侧不能通车，那么这辆货车在不碰杆的情况下，能从入口内通过吗？请你通过估算说明．（参考数据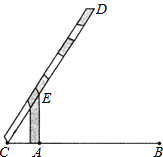： $\sqrt{3}$ ≈1.7）

查看试题解析
20. 如图，C为线段BD上的一个动点，分别过点B，D在BD两侧作BA⊥BD，DE⊥BD，连结AC，CE.已知AB=5，DE=9，BD=8，设BC= $x$ .

(1)、用含 $x$ 的代数式表示AC+CE的长.

(2)、当点C满足什么条件时，AC+CE的值最小?

(3)、根据(2)中的结论，请构图求出代数式 $\sqrt{x^{2} + 4} + \sqrt{(12 - x)^{2} + 9}$ 的最小值.

查看试题解析

四、综合题

21. 在一节数学课上，刘老师请同学心里想一个非零的有理数，然后把这个数按照下面的程序进行计算后，刘老师立刻说出计算结果．

(1)、小明同学心里想的数是8，列出了下面的算式，请你计算出最后的结果：[（8+2）²﹣（8﹣2）²]×（﹣25）÷8；

(2)、小明又试了几个数进行计算，发现结果都相等，于是小明把心里想的这个数记作a（a≠0），并按照程序通过计算进行验证，请你写出这个验证过程．

查看试题解析
22. 给某气球充满一定质量的气体，在温度不变时，气球内气体的气压 $p$ $（ K P a ）$ 是气体体积 $V$ （ $m^{3}$ ）的反比例函数，其图象如图所示．

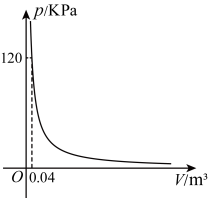(1)、当气球内的气压超过 $150 K P a$ 时，气球会爆炸．若将气球近似看成一个球体，试估计气球的半径至少为多少时气球不会爆炸（球体的体积公式 $V = \frac{4}{3} π r^{3}$ ， $π$ 取3）；

(2)、请你利用 $p$ 与 $V$ 的关系试解释为什么超载的车辆容易爆胎．

查看试题解析
23. 我们约定：若关于x的二次函数 $y_{1} = a_{1} x^{2} + b_{1} x + c_{1}$ 与 $y_{2} = a_{2} x^{2} + b_{2} x + c_{2}$ 同时满足 $\sqrt{a_{2} - c_{1}} + （ b_{2} + b_{1} ）^{2} + | c_{2} - a_{1} | = 0 ， b_{1} - {b_{2}}^{2023} \neq 0$ ，则称函数 $y_{1}$ 与函数 $y_{2}$ 互为“美美与共”函数．根据该约定，解答下列问题：

(1)、若关于x的二次函数 $y_{1} = 2 x^{2} + k x + 3$ 与 $y_{2} = m x^{2} + x + n$ 互为“美美与共”函数，求k，m，n的值；

(2)、对于任意非零实数r，s，点 $P (r ， t)$ 与点 $Q (s ， t) (r \neq s)$ 始终在关于x的函数 $y_{1} = x^{2} + 2 r x + s$ 的图像上运动，函数 $y_{1}$ 与 $y_{2}$ 互为“美美与共”函数．
①求函数 $y_{2}$ 的图像的对称轴；
②函数 $y_{2}$ 的图像是否经过某两个定点？若经过某两个定点，求出这两个定点的坐标；否则，请说明理由；

(3)、在同一平面直角坐标系中，若关于x的二次函数 $y_{1} = a x^{2} + b x + c$ 与它的“美美与共”函数 $y_{2}$ 的图像顶点分别为点A，点B，函数 $y_{1}$ 的图像与x轴交于不同两点C，D，函数 $y_{2}$ 的图像与x轴交于不同两点E，F．当 $C D = E F$ 时，以A，B，C，D为顶点的四边形能否为正方形？若能，求出该正方形面积的取值范围；若不请说明理由．

查看试题解析