浙江省杭州市第十五中学2023-2024学年九年级下学期3月月考数学试题
试卷更新日期:2024-05-10 类型:月考试卷
一、选择题(共10小题,满分30分,每小题3分)
-
1. 的结果是( )A、 B、 C、 D、2. tan45°的值等于( )A、 B、 C、 D、13. 下列图形中,不是中心对称图形的是( )A、圆 B、菱形 C、矩形 D、等边三角形4. 年春节期间,杭州东站一天的客流量为人次.将用科学记数法表示应为( )A、 B、 C、 D、5. 如图,一个几何体由5个大小相同的正方体搭成,则这个立体图形的俯视图是( )
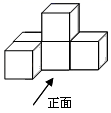 A、
A、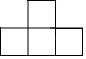 B、
B、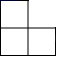 C、
C、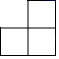 D、
D、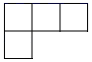 6. 如图,点是的劣弧上一点, , 则的度数为( )
6. 如图,点是的劣弧上一点, , 则的度数为( ) A、192° B、120° C、132° D、150°7. 若点 , , , 在反比例函数的图象上,则 , , 的大小关系是( )A、 B、 C、 D、8. 下图是甲乙丙三位同学在一次长跑练习中所用时间与路程之间的函数图象,其中最先到达终点和平均速度最快的分别是( )
A、192° B、120° C、132° D、150°7. 若点 , , , 在反比例函数的图象上,则 , , 的大小关系是( )A、 B、 C、 D、8. 下图是甲乙丙三位同学在一次长跑练习中所用时间与路程之间的函数图象,其中最先到达终点和平均速度最快的分别是( ) A、甲和乙 B、甲和丙 C、丙和甲 D、丙和乙9. 如图,已知正方形的边长为1,连接、 , 平分交于点 , 则长( )
A、甲和乙 B、甲和丙 C、丙和甲 D、丙和乙9. 如图,已知正方形的边长为1,连接、 , 平分交于点 , 则长( ) A、 B、 C、 D、10. 如图,抛物线与轴交于、两点,与轴交于点 , 且 , 是抛物线的顶点,三角形的面积等于1,则以下结论:①;②;③;④ , 其中正确的结论是( )
A、 B、 C、 D、10. 如图,抛物线与轴交于、两点,与轴交于点 , 且 , 是抛物线的顶点,三角形的面积等于1,则以下结论:①;②;③;④ , 其中正确的结论是( ) A、②④ B、①②④ C、①③④ D、①②③④
A、②④ B、①②④ C、①③④ D、①②③④二、填空题(共6小题,满分18分,每小题3分)
-
11. 化简: .12. 一个不透明的口袋中有除颜色外完全相同的5个小球.其中黄球有2个,红球有2个,蓝球有1个,随机摸出一个小球为红球的概率是 .13. 若把代数式化为的形式,其中 , 为常数,则 .14. 如图,是圆锥的高,是底面半径,如果圆锥底面周长为厘米, , 那么圆锥的高为 .
 15. 已知关于 , 的方程组 , 则 .16. 如图,中, , , 点D为AB的中点,点P为AC上一个动点,将沿DP折叠得到 , 点A的对应点为点Q , 当时,的度数为 .
15. 已知关于 , 的方程组 , 则 .16. 如图,中, , , 点D为AB的中点,点P为AC上一个动点,将沿DP折叠得到 , 点A的对应点为点Q , 当时,的度数为 .
三、解答题(共8小题,满分72分)
-
17. 下面是小清与小北两位同学解分式方程的过程:
小清:
去分母,得: ,
解得: ,
检验:当时, ,
∴分式方程的解为 .
小北:
去分母,得:
解得: ,
检验:当时, ,
∴分式方程无解.
请判断小清与小北的解法是否正确?如果不正确,写出你的解答过程.
18. 在全民读书月活动中,某校随机抽样调查了一部分学生本学期计划购买课外书的费用情况,根据图中的相关信息,解答下面问题; (1)、这次调查获取的样本容量是;(2)、由统计图可知,这次调查获取的样本数据的众数是;中位数是;(3)、若该校共有1000名学生,根据样本数据,估计该校本学期计划购买课外书的总花费.19. 如图,在 ABCD中,F是AD的中点,延长BC到点E,使CE= BC,连结DE,CF。
(1)、这次调查获取的样本容量是;(2)、由统计图可知,这次调查获取的样本数据的众数是;中位数是;(3)、若该校共有1000名学生,根据样本数据,估计该校本学期计划购买课外书的总花费.19. 如图,在 ABCD中,F是AD的中点,延长BC到点E,使CE= BC,连结DE,CF。 (1)、求证:四边形CEDF是平行四边形;(2)、若AB=4,AD=6,∠B=60°,求DE的长。20. 如图,为了测量某建筑物的高度,先在地面上用测角仪自处测得建筑物顶部的仰角 , 然后在水平地面上向建筑物走到B点处,此时自处测得建筑物顶部的仰角 . 已知测角仪的高度是 .
(1)、求证:四边形CEDF是平行四边形;(2)、若AB=4,AD=6,∠B=60°,求DE的长。20. 如图,为了测量某建筑物的高度,先在地面上用测角仪自处测得建筑物顶部的仰角 , 然后在水平地面上向建筑物走到B点处,此时自处测得建筑物顶部的仰角 . 已知测角仪的高度是 . (1)、若 , , ,计算出该建筑物的高度.(2)、若 , , , 计算出该建筑物的高度(用含 的代数式表示)21. 如图,中, , , D为边上一点, .
(1)、若 , , ,计算出该建筑物的高度.(2)、若 , , , 计算出该建筑物的高度(用含 的代数式表示)21. 如图,中, , , D为边上一点, . (1)、求证:;(2)、如果 , 求的长.22. 关于的一元二次方程有两个不相等的实数根.(1)、求的取值范围;(2)、当取满足条件的最大整数时,求方程的根.
(1)、求证:;(2)、如果 , 求的长.22. 关于的一元二次方程有两个不相等的实数根.(1)、求的取值范围;(2)、当取满足条件的最大整数时,求方程的根.

