浙江省台州市路桥区十校联盟2023-2024学年七年级下学期数学期中考试试卷

试卷更新日期：2024-05-10 类型：期中考试

进入出卷网下载

一、选择题：本大题有10个小题，每小题3分，共30分．在每小题给出的四个选项中，只有一项最符合题目要求

1. 下列各数中，是无理数的是（）

A、 $\sqrt{2}$ B、 $\sqrt{0.64}$ C、 $\frac{5}{3}$ D、1.414

查看试题解析
2. 如图，直线a，b被直线c所截，则∠1与∠2是（）

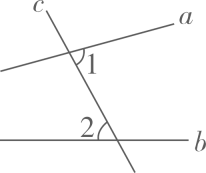A、对顶角 B、同位角 C、同旁内角 D、内错角

查看试题解析
3. 台风是一种破坏性极大的自然灾害，气象台为了预报台风，首先应确定台风中心的位置．下列表述能确定台风中心位置的是（）

A、在沿海地区 B、台湾省以东的洋面上 C、距离台州200km D、北纬28°，东经120°

查看试题解析
4. 下列各组数是方程 $x + y = 2$ 解的是（）

A、 ${\begin{array}{l} x = 2 \\ y = 0 \end{array}$ B、 ${\begin{array}{l} x = 1 \\ y = - 3 \end{array}$ C、 ${\begin{array}{l} x = 1 \\ y = 2 \end{array}$ D、 ${\begin{array}{l} x = 2 \\ y = 2 \end{array}$

查看试题解析
5. 在平面直角坐标系中，点 $P (- 2, 3)$ 位于（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
6. 利用加减消元法解方程组 ${\begin{array}{l} 2 x + 3 y = 6 ① \\ 5 x - 2 y = 9 ② \end{array}$ ，下列做法正确的是（）

A、要消去x ，可以将① $\times 5 +$ ② $\times 2$ B、要消去y ，可以将① $\times 5 -$ ② $\times 3$ C、要消去x ，可以将① $\times 5 -$ ② $\times 2$ D、要消去y ，可以将① $\times 2 -$ ② $\times 3$

查看试题解析
7. 若 $m = \sqrt{10} - 1$ ，则估计m的值所在范围是（）

A、 $1 < m < 2$ B、 $2 < m < 3$ C、 $3 < m < 4$ D、 $4 < m < 5$

查看试题解析
8. 如图，下列条件中能判断 $B C ∥ E F$ 的是（）
① $∠ 1 = ∠ E$ ② $∠ B = ∠ E$ ③ $∠ B = ∠ 2$ ④ $∠ E + ∠ E G C = 180 °$

A、①② B、①③ C、①④ D、①②④

查看试题解析
9. 在平面直角坐标系 $x O y$ 中，已知 $A (a, 0), B (1, - 2)$ ，那么线段 $A B$ 长度的最小值为（）

A、1 B、2 C、3 D、 $| a |$

查看试题解析
10. 有一个数值转换器，原理如图所示，若输出的y为 $\sqrt{3}$ 时，则输入的x值是（）

A、3 B、3或9 C、 $3^{n}$ （n为正整数） D、3或 $3^{2^{n}}$ （n为正整数）

查看试题解析

二、填空题：本大题有6个小题．每小题4分，共24分．

11. 3的平方根是

查看试题解析
12. 如图，从人行横道线上的点P处过马路，沿线路PB行走距离最短，其依据的几何学原理是.

查看试题解析
13. 要说明命题“一个正数的算术平方根一定小于这个数”是假命题，可以按以下举反例说明：当 $a =$ 时， $\sqrt{a} =$ ，得 $\sqrt{a}$ a ，所以这是一个假命题．

查看试题解析
14. 如图，把三角尺的直角顶点放在直尺的一边上，若 $∠ 1 = 160 °$ ，则 $∠ 2$ 的度数为．

查看试题解析
15. 我国民间流传着许多趣味算题，它们多以顺口溜的形式表达，其中《孙子算经》中记我了这样一个数学问题：一群老人去赶集，半路买了一堆梨，一人一个多一梨，一人两个少二梨，请问君子知道否，几个老人几个梨？若设有x个老人，y个梨，则可列出的方程组为．

查看试题解析
16. 在平面直角坐标系 $x O y$ 中，线段CD是由线段AB平移所得，已知 $A (- 3, 0), B (0, - 2), C (2, 0)$ ，则下列4个结论中，正确的有．（填序号）
① $A D ∥ B C$ ；② $∠ A D C = ∠ A B C$ ；③四边形ABCD的面积为10；④点D坐标为 $(- 1, 3)$ ．

查看试题解析

三、解答题：本大题有8个小题，共66分．解答应写出文字说明、证明过程或演算步骤．

17. 计算：

(1)、 $\sqrt{16} - \sqrt[3]{8} + \sqrt{\frac{1}{9}}$ ；

(2)、 $2 \sqrt{2} + | \sqrt{3} - \sqrt{2} |$ ．

查看试题解析
18. 解下列方程（组）：

(1)、 $(x - 1)^{2} = 25$ ；

(2)、 ${\begin{array}{l} 2 x - 3 y = 3 \\ x + 2 y = - 2 \end{array}$ ．

查看试题解析
19. 光线在不同介质中传播速度不同，从一种介质射向另一种介质时会发生折射．如图，水面 $A B$ 与水杯下沿 $C D$ 平行，光线 $E F$ 从空气射向水中时发生折射，光线变成 $F G$ ，点H在光线 $E F$ 所在的直线上，已知 $∠ E F A = 40 °, ∠ F G C = 61 °$ ，求 $∠ G F H$ 的度数．

查看试题解析
20. 如图，平面直角坐标系 $x O y$ 中，三角形 $A B C$ 的三个顶点坐标分别是 $A (4, 3), B (3, 1), C (1, 2)$ ，现将三角形 $A B C$ 平移，使点B与坐标原点O重合，点A与点 $A_{1}$ 重合，得到三角形 $A_{1} O C_{1}$ ．

(1)、画出三角形 $A_{1} O C_{1}$

(2)、写出点 $A_{1}, C_{1}$ 的坐标；

(3)、求三角形 $A_{1} O C_{1}$ 的面积：

查看试题解析
21. 如图，已知 $∠ A = ∠ B, A B ∥ C E$ ．求证： $C E$ 平分 $∠ A C D$ ．
证明： $∵ A B ∥ C E$ （    ），
$∠ B =$      ▲     （    ），
$∠ A =$      ▲  （    ），
$∵ ∠ A = ∠ B$ （已知），
$∴$      ▲  =     ▲  （等量代换）．
$∴ C E$ 平分 $∠ A C D$ （    ），

查看试题解析
22. 已知二元一次方程 $2 x + 5 y = 24$ ．

(1)、写出此方程的所有正整数解．

(2)、若二元一次方程组 ${\begin{array}{l} 2 x + 5 y = 24 \\ _________ \end{array}$ 存在x ， y互为相反数的解，请在横线处补上一个方程，并求出此方程组的解．

查看试题解析
23. 如图， $∠ A = 90 °$ ， $D$ 在 $A B$ 上， $C D$ 平分 $∠ A C B$ ， $M$ 是线段 $B D$ 上的点（不与 $B$ ， $D$ 重合），过点 $M$ 作 $M E ⊥ A B$ ，与 $B C$ 交于点 $E$ ，与直线 $C D$ 交于点 $F$ ．

(1)、依据题意补全图形：

(2)、若 $∠ C F E = 25 °$ ，则 $∠ B E F =$ $°$ ；

(3)、判断 $∠ C F E$ 与 $∠ B E F$ 有怎样的数量关系，并证明．

查看试题解析
24. 阅读下列材料：
我们知道，二元一次方程 $x - y = - 2$ 有无数组解，若我们把每一组解用有序数对 $(x, y)$ 表示，就可以标出一些以方程 $x - y = - 2$ 的解为坐标的点，过这些点中的任意两点可以作一条直线，发现其它点也都在这条直线上．反之，在这条直线上任意取一点，发现这个点的坐标是方程 $x - y = - 2$ 的解．我们把以方程 $x - y = - 2$ 的解为坐标的所有点组成的图形叫做方程 $x - y = - 2$ 的图象，记作直线 $l_{1}$ ．
请解答以下问题：

(1)、在所给的平面直角坐标系 $x O y$ 中描出点 $A (- 1, 1)$ ，并计算说明点A在方程 $x - y = - 2$ 的图象 $l_{1}$ 上；

(2)、在所给的平面直角坐标系 $x O y$ 中画出方程 $2 x + y = 5$ 的图象 $l_{2}$ ；

(3)、若直线 $l_{1}$ 与（2）中的 $l_{2}$ 相交于点B ，求点B的坐标；

(4)、结合坐标网格，直接写出 $O A$ ， $O B$ 的长度．

查看试题解析