浙江省宁波市北仑区精准联盟2023-2024年八年级下学期数学期中考试试卷

试卷更新日期：2024-05-10 类型：期中考试

进入出卷网下载

一、选择题（每小题3分，共30分）

1. “琴棋书画”的棋是指围棋，围棋起源于中国，至今已有四千多年的历史．下列由黑、白棋子摆成的图案中，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列各式中，正确的是（　　）

A、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ B、 $\sqrt{12} = 4 \sqrt{3}$ C、 $\sqrt{2} \times \sqrt{3} = 6$ D、 $\frac{\sqrt{12}}{\sqrt{2}} = \sqrt{6}$

查看试题解析
3. 甲、乙、丙、丁四个小组的同学参加了班里组织的中华古诗词知识竞赛，在相同条件下各小组的成绩情况如表格所示，若要从中选择出一个最优秀的小组参加年级的比赛，那么应选（）

甲
乙
丙
丁
平均分
87
90
88
90
方差
3.5
3.5
4
4.2

A、甲组 B、乙组 C、丙组 D、丁组

查看试题解析
4. 用配方法解方程 $x^{2} - 6 x - 4 = 0$ ，下列配方正确的是（）

A、 $(x + 3)^{2} = 13$ B、 $(x - 3)^{2} = 13$ C、 $(x - 6)^{2} = 4$ D、 $(x - 3)^{2} = 5$

查看试题解析
5. 如图，四边形 $A B C D$ 是平行四边形，添加下列条件，能判定这个四边形是矩形的是（）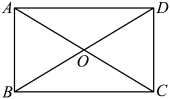

A、 $∠ B A D = ∠ A B C$ B、 $A B ⊥ B D$ C、 $A C ⊥ B D$ D、 $A B = B C$

查看试题解析
6. 用反证法证明“四边形至少有一个角是钝角或直角”时，应先假设（）

A、四边形中每个角都是锐角 B、四边形中每个角都是钝角或直角 C、四边形中有三个角是锐角 D、四边形中有三个角是钝角或直角

查看试题解析
7. 如图，平行四边形纸片ABCD和EFGH上下叠放， $A D ∥ E H$ 且 $A D = E H$ ， CE交GH于点O ，已知 $S_{▱ A B C D} = a, S_{▱ E F G H} = b (a < b)$ ，则阴影部分面积S为（）

A、 $\frac{1}{2} a$ B、 $\frac{1}{2} (b - a)$ C、 $\frac{1}{2} b$ D、 $b - a$

查看试题解析
8. 如图，在矩形ABCD中，AD＝3，AB＝4，M为线段BD上一动点，MP⊥CD于点P，MQ⊥BC于点Q，则PQ的最小值为（）

A、 $\frac{12}{5}$ B、3 C、 $\frac{24}{5}$ D、 $\frac{5}{2}$

查看试题解析
9. 对于一元二次方程 $a x^{2} + b x + c = 0 (a \neq 0)$ ，下列说法：
①若 $a + b + c = 0$ ，则 $b^{2} - 4 a c \geq 0$ ；
②若方程 $a x^{2} + c = 0$ 有两个不相等的实根，则方程 $a x^{2} + b x + c = 0$ 必有两个不相等的实根；
③若c是方程 $a x^{2} + b x + c = 0$ 的一个根，则一定有 $a c + b + 1 = 0$ 成立；
④若 $x_{0}$ 是一元二次方程 $a x^{2} + b x + c = 0$ 的根，则 $b^{2} - 4 a c = {(2 a x_{0} + b)}^{2}$ .
其中正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
10. 如图，点E是矩形ABCD内一点，连结AE，DE，AC，EC，BE，知道下列哪个选项的值就能要求△AEC的面积（）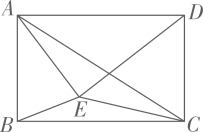

A、△ABE与△BEC面积之差 B、△ADE与△BEC面积之差 C、△DEC与△BEC面积之差 D、△ADC与△DEC面积之差

查看试题解析

二、填空题（每小题4分，共24分）

11. 要使 $\sqrt{2 x - 6}$ 有意义，则x的取值范围为.

查看试题解析
12. 一个多边形的每一个外角都等于72°，则这个多边形是边形．

查看试题解析
13. 已知a ， b是方程 $x^{2} + 3 x - 5 = 0$ 的两个实数根，则 $a^{2} - 3 b + 2020$ 的值是。

查看试题解析
14. 如图，在 $R t △ A B C$ 中， $∠ A C B = 90 ° ， A C = B C = 3$ ，点D在边AC上， $A D = 1$ ，过点D作 $D E ∥ A B$ 交边BC于点E ，连接BD ，点O是线段BD的中点，连接OE ，则OE的长为。

查看试题解析
15. 如图，已知四边形ABCD和四边形BCEF均为平行四边形， $∠ D = 60 °$ ，连接AF ，并延长交BE于点P ，若 $A P ⊥ B E ， A B = 3 ， B C = 2 ， A F = 1$ ，则BE的长为．

查看试题解析
16. 如图，在矩形ABCD中， $A B = \sqrt{3} ， B C = 1$ ，将 $△ A B D$ 沿射线DB平移得到 $△ A^{'} B^{'} D^{'}$ ，连接 $B^{'} C$ ， $D^{'} C$ ，则 $B^{'} C + D^{'} C$ 的最小值是。

查看试题解析

三、解答题（本大题共8小题，共66分）

17.

(1)、计算题： $\sqrt{(- 3)^{2}} + \sqrt[3]{27} - \sqrt{\frac{16}{9}}$ ；

(2)、解方程： $x^{2} - 4 x - 3 = 0$ 。

查看试题解析
18. 作图题
图①、图②均为 $7 \times 6$ 的正方形网格，点A、B、C在格点上．
图① 图②

(1)、在图①中确定格点D ，并画出以A、B、C、D为顶点的四边形，使其为轴对称图形．（画一个即可）

(2)、在图②中确定格点E ，并画出以A、B、C、E为顶点的四边形，使其为中心对称图形．（画一个即可）

查看试题解析
19. 先化简，再求值： $a + \sqrt{1 - 2 a + a^{2}}$ ，其中 $a = 1007$ ．
如图是小亮和小芳的解答过程．
解：原式 $= a + \sqrt{(1 - a)^{2}}$
$= a + 1 - a$
$= 1$
解：原式 $= a + \sqrt{(1 - a)^{2}}$
$= a + a - 1$
$= 2013$

(1)、的解答过程是错误的；

(2)、先化简，再求值： $m + 2 \sqrt{m^{2} - 6 m + 9}$ ，其中 $m = - 2024$ ．

查看试题解析
20. 已知关于x的方程 $x^{2} - 7 x + (12 - a) = 0$ 有两个不相等的实数根．

(1)、求a的取值范围；

(2)、当a取满足条件的最小整数值时，求方程的根．

查看试题解析
21. 某学校从九年级同学中任意选取40人，随机分成甲、乙两个小组（每组20人）进行“引体向上”体能测试，根据测试成绩绘制出下面的统计表和统计图．
甲组成绩统计表
成绩
7
8
9
10
人数
1
9
5
5
乙组成绩统计图
请根据上面的信息，解答下列问题：

(1)、甲组成绩的中位数是，乙组成绩的众数是；

(2)、请求出乙组成绩的平均数；

(3)、已知甲组成绩的方差为 $S_{甲}^{2} = 0 ． 81$ ，请求乙组成绩的方差，并判断哪个小组的成绩更加稳定．

查看试题解析
22. 如图，将 $▱ A B C D$ 的边AB延长到点E ，使 $B E = A B$ ，连结DE ，交边BC于点F ．

(1)、求证： $△ B E F ≌ △ C D F$ ．

(2)、连结BD ， CE ．若 $∠ B F D = 2 ∠ A$ ，求证：四边形BECD是矩形．

查看试题解析

23. 根据以下素材，探索完成任务．

如何设计实体店背景下的网上销售价格方案？
素材1	某公司在网上和实体店同时销售一种自主研发的小商品，成本价为40元/件．
素材2	该商品的网上销售价定为60元/件，平均每天销售量是200件，在实体店的销售价定为80元/件，平均每天销售量是100件．按公司规定，实体店的销售价保持不变，网上销售价可按实际情况进行适当调整，需确保网上销售价始终高于成本价．
素材3	据调查，网上销售价每降低1元，网上销售每天平均多售出20件，实体店的销售受网上影响，平均每天销售量减少2件，
问题解决
任务1	计算所获利润	当该商品网上销售价为50元/件时，求公司在网上销售该商品每天的毛利润与实体店销售该商品每天的毛利润各是多少元？
任务2	拟定价格方案	公司要求每天的总毛利润（总毛利润=网上毛利润+实体店毛利润）达到8160元，求每件商品的网上销售价是多少元？

查看试题解析

24. 在平行四边形ABCD中，点O是对角线BD的中点，点E在边BC上，EO的延长线与边AD交于点F ，连接BF、DE如图1．

(1)、求证：四边形BEDF是平行四边形；

(2)、若 $D E = D C ， ∠ C B D = 45 °$ ，过点C作DE的垂线，与DE、BD、BF分别交于点G、H、P如图2．
①当 $C D = 6$ ． $C E = 4$ 时，求BE的长；
②求证： $C D = C H$ ．

查看试题解析

	甲	乙	丙	丁
平均分	87	90	88	90
方差	3.5	3.5	4	4.2

成绩	7	8	9	10
人数	1	9	5	5