2024年江苏省苏州市中考数学仿真模拟卷
试卷更新日期:2024-05-10 类型:中考模拟
一、选择题:本大题共8小题,每小题3分,共24分.在每小题给出的四个选项中,只有一项是符合题目要求的.请将选择题的答案用rId8铅笔涂在答题卡相对应的位置上.
-
1. 如图,数轴上点A所表示的数的相反数为( )
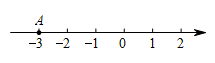 A、-3 B、3 C、 D、2. 在以下四个标志中,既是轴对称图形又是中心对称图形的有( )A、
A、-3 B、3 C、 D、2. 在以下四个标志中,既是轴对称图形又是中心对称图形的有( )A、 B、
B、 C、
C、 D、
D、 3. 如图:能判断 的条件是 )
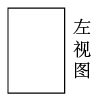
3. 如图:能判断 的条件是 )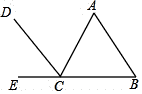 A、 B、 C、 D、4. 如图,是一个正三棱柱的三视图,则这个三棱柱摆放方式正确的是( )
A、 B、 C、 D、4. 如图,是一个正三棱柱的三视图,则这个三棱柱摆放方式正确的是( )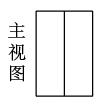
 A、
A、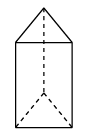 B、
B、 C、
C、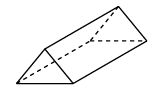 D、
D、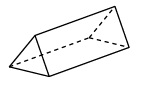 5. 下列运算正确的是( )A、 B、 C、 D、6. 一只小狗在如图的方砖上走来走去,最终停在阴影方砖上的概率是( )
5. 下列运算正确的是( )A、 B、 C、 D、6. 一只小狗在如图的方砖上走来走去,最终停在阴影方砖上的概率是( )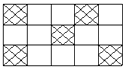 A、 B、 C、 D、7. 如图,O为坐标原点,△ABO的两个顶点A(6,0),B(6,6),点D在边AB上,AD=5BD,点C为OA的中点,点P为边OB上的动点,则使四边形PCAD周长最小的点P的坐标为( )
A、 B、 C、 D、7. 如图,O为坐标原点,△ABO的两个顶点A(6,0),B(6,6),点D在边AB上,AD=5BD,点C为OA的中点,点P为边OB上的动点,则使四边形PCAD周长最小的点P的坐标为( ) A、(3,3) B、( , ) C、( , ) D、(5,5)8. 如图①,在矩形 中,当直角三角板 的直角顶点 在 上移动时,直角边 始终经过点 ,设直角三角板的另一直角边 与 相交于点 .在运动过程中线段 的长度为 ,线段 的长为 , 与 之间的函数关系如图②所示.则 的长为( )
A、(3,3) B、( , ) C、( , ) D、(5,5)8. 如图①,在矩形 中,当直角三角板 的直角顶点 在 上移动时,直角边 始终经过点 ,设直角三角板的另一直角边 与 相交于点 .在运动过程中线段 的长度为 ,线段 的长为 , 与 之间的函数关系如图②所示.则 的长为( ) A、2.25 B、3 C、4 D、6
A、2.25 B、3 C、4 D、6二、填空题:本大题共8小题,每小题3分,共24分.把答案直接填在答题卡相对应的位置上.
-
9. 从0到9这10个自然数中随机取一个数,能使 有意义的概率是.10. 因式分解: .11. 解方程: 的解是 .12. 第七次全国人口普查结果显示,我国具有大学文化程度的人口超218000000人.数据218000000用科学记数法表示为.13. 要表示一个家庭一年用于“教育”, “服装”,“食品”,“其他”这四项的支出各占家庭本年总支出的百分比,从“扇形统计图”,“条形统计图”,“折线统计图”中选择一种统计图,最适合的统计图是.14. 如果A(﹣1,2),B(2,﹣1),C(m,m)三点在同一条直线上,则m的值等于.15. 若一个圆锥体的底面积是其表面积的 , 则其侧面展开图圆心角的度数为 .16. 如图, 中, , , , 绕顶点O逆时针旋转到 处,此时线段 与BO的交点E为BO的中点,则线段 的长度为.

三、解答题:本大题共11小题,共82分.把解答过程写在答题卡相对应的位置上,解答时应写出必要的计算过程、推演步骤或文字说明.作图时用2B铅笔或黑色墨水签字笔.
-
17. 计算:18. 解不等式组:19. 先化简再求值:(a+1﹣)÷ , 其中a是方程x2+2x﹣3=0的根.20. 如图,在菱形ABCD中,点E,F分别是边AD,AB的中点.
 (1)、求证:△ABE≌△ADF;(2)、若BE= ,∠C=60°,求菱形ABCD的面积.21. 在一个不透明的袋子中,放有四张质地完全相同的卡片,分别标有数字“-3, -2,1, 6”。(1)、随机抽出一张卡片是负数的概率是;(2)、第一次从袋中随机地抽出一张卡片,把所抽到的数字记为横坐标m,不放回袋中,再随机地从中抽出一张,把所抽到的数字记为纵坐标n。请用数状图或列表法求所得的点(m, n)在反比例函.数y= 上的概率。22. 为了解某校学生的身高情况,随机抽取该校男生、女生进行抽样调查.已知抽取的样本中,男生、女生的人数相同,利用所得数据绘制如下统计图表:
(1)、求证:△ABE≌△ADF;(2)、若BE= ,∠C=60°,求菱形ABCD的面积.21. 在一个不透明的袋子中,放有四张质地完全相同的卡片,分别标有数字“-3, -2,1, 6”。(1)、随机抽出一张卡片是负数的概率是;(2)、第一次从袋中随机地抽出一张卡片,把所抽到的数字记为横坐标m,不放回袋中,再随机地从中抽出一张,把所抽到的数字记为纵坐标n。请用数状图或列表法求所得的点(m, n)在反比例函.数y= 上的概率。22. 为了解某校学生的身高情况,随机抽取该校男生、女生进行抽样调查.已知抽取的样本中,男生、女生的人数相同,利用所得数据绘制如下统计图表:身高情况分组表(单位:cm)
组别
身高
A
x<155
B
155≤x<160
C
160≤x<165
D
165≤x<170
E
x≥170

根据图表提供的信息,回答下列问题:
(1)、样本中,男生的身高众数在组,中位数在组;(2)、样本中,女生身高在E组的人数有人;(3)、已知该校共有男生400人,女生380人,请估计身高在160≤x<170之间的学生约有多少人?23. 如图,公园里有一棵大树( )与一棵小树( ),受测量工具、地理环境及安全等因素影响不能直接测量它们的高度之差,小明与小丽手中有一副含 角的直角三角尺和一根皮尺,小明首先在与树根B、D成一条直线的点E处用三角尺测得小树 顶部C的仰角为 ,然后他向后移动调整,在M处用三角尺测得大树 顶部A的仰角也是 ,点M仍然与B、D在一条直线上,然后他俩用皮尺测得 米, 米,求两棵树的高度之差. 24. 环保局对某企业排污情况进行检测,结果显示,所排污水中硫化物的浓度超标,即硫化物的浓度超过最高允许的1.0mg/L,环保局要求该企业立即整改,在15天以内(含15天)排污达标,整改过程中,所排污水中硫化物的浓度γ(mg/L)与时间x(天)的变化规律如图所示,其中线段AB表示前3天的变化规律,从第3天起,所排污水中硫化物的浓度γ与时间x成反比例关系
24. 环保局对某企业排污情况进行检测,结果显示,所排污水中硫化物的浓度超标,即硫化物的浓度超过最高允许的1.0mg/L,环保局要求该企业立即整改,在15天以内(含15天)排污达标,整改过程中,所排污水中硫化物的浓度γ(mg/L)与时间x(天)的变化规律如图所示,其中线段AB表示前3天的变化规律,从第3天起,所排污水中硫化物的浓度γ与时间x成反比例关系 (1)、求整改过程中硫化物的浓度γ与时间x的函数表达式(要求标注自变量x的取值范围)(2)、该企业所排污水中硫化物的浓度,能否在15天以内(含15天)排污达标?为什么?25. 如图, 为 的直径,C为 上一点,连接 ,D是 上的一点,CD=BD, 与 、 分别交于点E、F.
(1)、求整改过程中硫化物的浓度γ与时间x的函数表达式(要求标注自变量x的取值范围)(2)、该企业所排污水中硫化物的浓度,能否在15天以内(含15天)排污达标?为什么?25. 如图, 为 的直径,C为 上一点,连接 ,D是 上的一点,CD=BD, 与 、 分别交于点E、F. (1)、求证: ;(2)、求证: ;(3)、若 ,求 的值.26. 一队学生从学校出发去劳动基地,行进的路程与时间的函数图象如图所示,队伍走了0.8小时后,队伍中的通讯员按原路加快速度返回学校取材料.通讯员经过一段时间回到学校,取到材料后立即按返校时加快的速度追赶队伍,并比学生队伍早18分钟到达基地.如图,线段OD表示学生队伍距学校的路程y(千米)与时间x(小时)之间的函数关系,折线OABC表示通讯员距学校的路程y(千米)与时间x(小时)之间的函数关系,请你根据图象信息,解答下列问题:
(1)、求证: ;(2)、求证: ;(3)、若 ,求 的值.26. 一队学生从学校出发去劳动基地,行进的路程与时间的函数图象如图所示,队伍走了0.8小时后,队伍中的通讯员按原路加快速度返回学校取材料.通讯员经过一段时间回到学校,取到材料后立即按返校时加快的速度追赶队伍,并比学生队伍早18分钟到达基地.如图,线段OD表示学生队伍距学校的路程y(千米)与时间x(小时)之间的函数关系,折线OABC表示通讯员距学校的路程y(千米)与时间x(小时)之间的函数关系,请你根据图象信息,解答下列问题: (1)、图中的 千米, 小时,点B的坐标为;(2)、求通讯员距学校的路程y(千米)与时间x(小时)之间的函数关系式;(3)、若通讯员与学生队伍的距离不超过3千米时能用无线对讲机保持联系,请你直接写出通讯员离开队伍后他们能用对讲机保持联系的时间的取值范围.
(1)、图中的 千米, 小时,点B的坐标为;(2)、求通讯员距学校的路程y(千米)与时间x(小时)之间的函数关系式;(3)、若通讯员与学生队伍的距离不超过3千米时能用无线对讲机保持联系,请你直接写出通讯员离开队伍后他们能用对讲机保持联系的时间的取值范围.答: .
27. 如图,在矩形中, , .点P从点A出发以每秒2个单位的速度沿运动,到点A停止.在点P运动的同时,点Q从点A出发以每秒1个单位的速度沿运动.当点P回到点A停止时,点Q也随之停止运动.设点P的运动时间为t秒. (1)、用含t的代数式表示线段的长.(2)、以为边作矩形 , 使点M与点A在所在直线的两侧,且.
(1)、用含t的代数式表示线段的长.(2)、以为边作矩形 , 使点M与点A在所在直线的两侧,且.①当点Q在边上,且点M落在上时,求t的值.
②当点M在矩形内部时,直接写出t的取值范围.
(3)、点E在边上,且.在线段上只存在一点F,使 , 直接写出t的取值范围.