2024年中考数学精选压轴题之四边形综合探究(一)
试卷更新日期:2024-05-10 类型:三轮冲刺
一、解答题
-
1. 如图,已知正方形ABCD , AB=8,点M为射线DC上的动点,射线AM交BD于E , 交射线BC于F , 过点C作CQ⊥CE , 交AF于点Q .
 (1)、当BE=2DE时,求DM的长.(2)、当M在线段CD上时,若CQ=3,求MF的长.(3)、①当DM=2CM时,作点D关于AM的对称点N , 求tan∠NAB的值.
(1)、当BE=2DE时,求DM的长.(2)、当M在线段CD上时,若CQ=3,求MF的长.(3)、①当DM=2CM时,作点D关于AM的对称点N , 求tan∠NAB的值.②若BE=4DE , 直接写出△CQE与△CMF的面积比 .
2. 对于一个四边形给出如下定义:有一组对角相等且有一组邻边相等,则称这个四边形为奇特四边形. (1)、命题“另一组邻边也相等的奇特四边形为正方形”是(真或假)命题.(2)、如图,在正方形ABCD中,E是AB边上一点,F是AD延长线一点, , 连接EF , EC , FC , 取EF的中点G , 连接CG并延长交AD于点H . 探究:四边形BCGE是否是奇特四边形,如果是证明你的结论,如果不是请说明理由.(3)、在(2)的条件下,若四边形BCGE的面积为16,则的值是多少?3. 如图,的对角线 , 交于点O , 平分 , 交于点E , 且.
(1)、命题“另一组邻边也相等的奇特四边形为正方形”是(真或假)命题.(2)、如图,在正方形ABCD中,E是AB边上一点,F是AD延长线一点, , 连接EF , EC , FC , 取EF的中点G , 连接CG并延长交AD于点H . 探究:四边形BCGE是否是奇特四边形,如果是证明你的结论,如果不是请说明理由.(3)、在(2)的条件下,若四边形BCGE的面积为16,则的值是多少?3. 如图,的对角线 , 交于点O , 平分 , 交于点E , 且. (1)、求证:;(2)、若 , , 连接;
(1)、求证:;(2)、若 , , 连接;①若 , 求平行四边形的面积;
②设 , 试求k与m满足的关系.
4. 在平行四边形中, , , . (1)、若 , 则;(2)、如图 , 当时,求对角线的长(用含的式子表示);(3)、如图 , 四边形 , 四边形都是平行四边形,延长交于点 , 若 , , , , 求的长.5. 在△ABC中,AC=BC , 点D是边AB上不与点B重合的一动点,将△BDC绕点D旋转得到△EDF , 点B的对应点E落在直线BC上,EF与AC相交于点G , 连接AF .
(1)、若 , 则;(2)、如图 , 当时,求对角线的长(用含的式子表示);(3)、如图 , 四边形 , 四边形都是平行四边形,延长交于点 , 若 , , , , 求的长.5. 在△ABC中,AC=BC , 点D是边AB上不与点B重合的一动点,将△BDC绕点D旋转得到△EDF , 点B的对应点E落在直线BC上,EF与AC相交于点G , 连接AF . (1)、如图1,当点D与点A重合时,
(1)、如图1,当点D与点A重合时,①求证:∠C=∠CEF;
②判断AF与BC的位置关系是 ▲ ;
(2)、如图2,当点D不与点A重合,点E在边BC上时,判断AF与BC的位置关系,并写出证明过程;(3)、如图3,当点D是AB的中点,点E在边BC上时,延长BA , CF相交于点P , 若AB=CD=2,求PF的长.6. 如图 , 在矩形中, , , 点在边上,且 , 动点从点出发,沿折线以每秒个单位长度的速度运动,作 , 交边或边于点 , 连接 , 当点与点重合时,点停止运动设点的运动时间为秒 (1)、当点和点重合时,线段的长为;(2)、当点和点重合时,求的比值是多少?(3)、当点在边上运动时,的形状始终是等腰直角三角形,如图 , 请说明理由;(4)、作点关于直线的对称点 , 连接、 , 当四边形和矩形重叠部分图形为轴对称四边形时,请直接写出的取值范围.7. 如图,在矩形中, , , 对角线 , 交于点点从点出发,沿方向匀速运动速度为;同时,点从点出发,沿方向匀速运动,速度为;当一个点停止运动时,另一个点也停止运动连接并延长交于点 , 过点作 , 交于点 , 设运动时间为 , 解答下列问题:
(1)、当点和点重合时,线段的长为;(2)、当点和点重合时,求的比值是多少?(3)、当点在边上运动时,的形状始终是等腰直角三角形,如图 , 请说明理由;(4)、作点关于直线的对称点 , 连接、 , 当四边形和矩形重叠部分图形为轴对称四边形时,请直接写出的取值范围.7. 如图,在矩形中, , , 对角线 , 交于点点从点出发,沿方向匀速运动速度为;同时,点从点出发,沿方向匀速运动,速度为;当一个点停止运动时,另一个点也停止运动连接并延长交于点 , 过点作 , 交于点 , 设运动时间为 , 解答下列问题: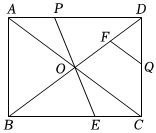 (1)、当为何值时,是等腰三角形;
(1)、当为何值时,是等腰三角形;
(2)、设五边形的面积为 , 试确定与的函数关系式;
(3)、在运动过程中,当::时直接写出的值.8. 已知:在矩形中,把矩形绕点旋转,得到矩形 , 且点落在边上,连接交于点 . (1)、如图 , 连接 .
(1)、如图 , 连接 .求证:平分;
求证:是的中点;
(2)、如图 , 连接 , 若平分 , , 求的长.9. 在中,B在C的左边, , 将关于作轴对称,得四边形 . P是对角线上的动点 , E是直线上的动点 , 且 . (1)、四边形如图1所示,四边形是(填“矩形”或“菱形”或“正方形”);(填“”或“”);(2)、四边形如图2所示,且 , 四边形是 ▲ (填“矩形”或“菱形”或“正方形”);(1)中与之间的数量关系还成立吗?若成立,请说明理由.(3)、四边形如图3所示,若 , , 请直接写出的度数.(用含、的代数式表示)10. 如图1,在边长为2的正方形中,点是射线上一动点,连接 , 以为边在直线右侧作正方形 .
(1)、四边形如图1所示,四边形是(填“矩形”或“菱形”或“正方形”);(填“”或“”);(2)、四边形如图2所示,且 , 四边形是 ▲ (填“矩形”或“菱形”或“正方形”);(1)中与之间的数量关系还成立吗?若成立,请说明理由.(3)、四边形如图3所示,若 , , 请直接写出的度数.(用含、的代数式表示)10. 如图1,在边长为2的正方形中,点是射线上一动点,连接 , 以为边在直线右侧作正方形 .图1
 图2
图2 (1)、当点在线段上,连接 , 求证:;(2)、当点是线段中点,连接 , 求线段的长;(3)、如图2,点在线段的延长线上,连接 , 若的延长线恰好经过的中点 , 求线段的长.11. 如图,在矩形中, , , 点E是边上一点,连接 , 将沿折叠得到 , 边 , 分别交于点M , N .
(1)、当点在线段上,连接 , 求证:;(2)、当点是线段中点,连接 , 求线段的长;(3)、如图2,点在线段的延长线上,连接 , 若的延长线恰好经过的中点 , 求线段的长.11. 如图,在矩形中, , , 点E是边上一点,连接 , 将沿折叠得到 , 边 , 分别交于点M , N . (1)、求证:;(2)、当时.
(1)、求证:;(2)、当时.①求BE的长;
②若点P是边上的动点,连接 , 过点A作的垂线交线段于点Q , 试探究的值是否发生变化,若变化,请说明理由;若不变,请求出的值.
12. 如图,和分别位于两侧,为中点,连接 , . (1)、如图1,若 , 求的长;(2)、如图2,连接交于点F,在上取一点G使得 . 若 , . 猜想与之间存在的数量关系,并证明你的猜想;(3)、如图3,是以为斜边的等腰直角三角形,若 , , 请直接写出当取最大值时的面积.
(1)、如图1,若 , 求的长;(2)、如图2,连接交于点F,在上取一点G使得 . 若 , . 猜想与之间存在的数量关系,并证明你的猜想;(3)、如图3,是以为斜边的等腰直角三角形,若 , , 请直接写出当取最大值时的面积.二、实践探究题
-
13.
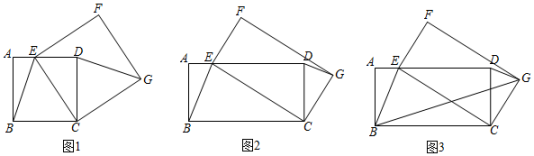 (1)、【问题情境】如图1,四边形ABCD是正方形,点E是AD边上的一个动点,以CE为边在CE的右侧作正方形CEFG,连接DG、BE,则DG与BE的数量关系是;(2)、【类比探究】
(1)、【问题情境】如图1,四边形ABCD是正方形,点E是AD边上的一个动点,以CE为边在CE的右侧作正方形CEFG,连接DG、BE,则DG与BE的数量关系是;(2)、【类比探究】如图2,四边形ABCD是矩形,AB=2,BC=4,点E是AD边上的一个动点,以CE为边在CE的右侧作矩形CEFG,且CG:CE=1:2,连接DG、BE.判断线段DG与BE有怎样的数量关系和位置关系,并说明理由;
(3)、【拓展提升】如图3,在(2)的条件下,连接BG,则2BG+BE的最小值为 .
14. 综合与实践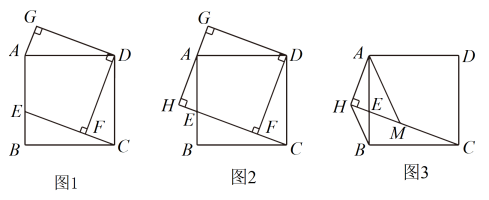 (1)、【思考尝试】
(1)、【思考尝试】数学活动课上,老师出示了一个问题:如图1,在矩形ABCD中,E是边上一点,于点F, , , . 试猜想四边形的形状,并说明理由;
(2)、【实践探究】小睿受此问题启发,逆向思考并提出新的问题:如图2,在正方形中,E是边上一点,于点F,于点H,交于点G,可以用等式表示线段 , , 的数量关系,请你思考并解答这个问题;
(3)、【拓展迁移】小博深入研究小睿提出的这个问题,发现并提出新的探究点:如图3,在正方形中,E是边上一点,于点H,点M在上,且 , 连接 , , 可以用等式表示线段 , 的数量关系,请你思考并解答这个问题.
15. 某校数学活动小组探究了如下数学问题: (1)、问题发现:如图1,中, , . 点P是底边上一点,连接 , 以为腰作等腰 , 且 , 连接、则和的数量关系是;(2)、变式探究:如图2,中, , . 点P是腰上一点,连接 , 以为底边作等腰 , 连接 , 判断和的数量关系,并说明理由;(3)、问题解决:如图3,在正方形中,点是边上一点,以为边作正方形 , 点
(1)、问题发现:如图1,中, , . 点P是底边上一点,连接 , 以为腰作等腰 , 且 , 连接、则和的数量关系是;(2)、变式探究:如图2,中, , . 点P是腰上一点,连接 , 以为底边作等腰 , 连接 , 判断和的数量关系,并说明理由;(3)、问题解决:如图3,在正方形中,点是边上一点,以为边作正方形 , 点是正方形两条对角线的交点,连接 . 若正方形的边长为 , , 请直接写出正方形的边长.
16. 综合与探究.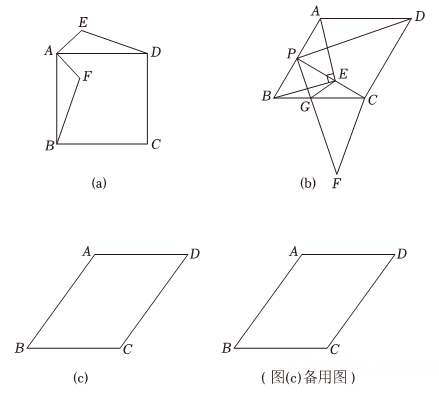 (1)、【特例感知】
(1)、【特例感知】如图(a),E是正方形ABCD外一点,将线段AE绕点A顺时针旋转得到AF , 连接DE , BF . 求证:;
(2)、【类比迁移】如图(b),在菱形ABCD中, , P是AB的中点,将线段PA , PD分别绕点P顺时针旋转得到PE , PF , PF交BC于点G , 连接CE , CF , 求四边形CEGF的面积:
(3)、【拓展提升】如图(c),在平行四边形ABCD中,为锐角且满足 . P是射线BA上一动点,点C , D同时绕点P顺时针旋转得到点 , , 当为直角三角形时,直接写出BP的长.
17. 【操作与发现】
如图①,在正方形ABCD中,点N,M分别在边BC、CD上.连接AM、AN、MN.∠MAN=45°,将△AMD绕点A顺时针旋转90°,点D与点B重合,得到△ABE.易证:△ANM≌△ANE,从而可得:DM+BN=MN.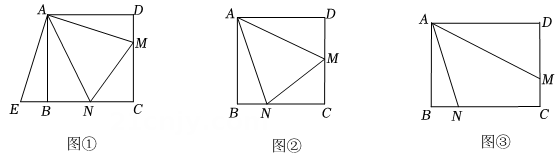 (1)、【实践探究】在图①条件下,若CN=6,CM=8,正方形ABCD的边长是 .(2)、如图②,在正方形ABCD中,点M、N分别在边DC、BC上,连接AM、AN、MN,∠MAN=45°,若tan∠BAN= , ,求证:M是CD的中点.(3)、【拓展】如图③,在矩形ABCD中,AB=12,AD=16,点M、N分别在边DC、BC上,连接AM、AN,已知∠MAN=45°,BN=4,则DM的长是 .18. 问题提出:如图(1),是菱形边上一点,是等腰三角形, , , 交于点 , 探究与的数量关系.问题探究:
(1)、【实践探究】在图①条件下,若CN=6,CM=8,正方形ABCD的边长是 .(2)、如图②,在正方形ABCD中,点M、N分别在边DC、BC上,连接AM、AN、MN,∠MAN=45°,若tan∠BAN= , ,求证:M是CD的中点.(3)、【拓展】如图③,在矩形ABCD中,AB=12,AD=16,点M、N分别在边DC、BC上,连接AM、AN,已知∠MAN=45°,BN=4,则DM的长是 .18. 问题提出:如图(1),是菱形边上一点,是等腰三角形, , , 交于点 , 探究与的数量关系.问题探究: (1)、先将问题特殊化,如图(2),当时,直接写出的大小;(2)、再探究一般情形,如图(1),求与的数量关系;(3)、问题拓展将图(1)特殊化,如图(3),当时,若 , 求的值.19.
(1)、先将问题特殊化,如图(2),当时,直接写出的大小;(2)、再探究一般情形,如图(1),求与的数量关系;(3)、问题拓展将图(1)特殊化,如图(3),当时,若 , 求的值.19. (1)、【问题探究】如图1,正方形ABCD中,点F、G分别在边BC、CD上,且AF⊥BG于点P , 求证:AF=BG;(2)、【知识迁移】如图2,矩形ABCD中,AB=4,BC=8,点E、F、G、H分别在边AB、BC、CD、AD上,且EG⊥FH于点P . 若EG•HF=48,求HF的长;(3)、【拓展应用】如图3,在菱形ABCD中,∠ABC=60°,AB=6,点E在直线AB上,BE=4,AF⊥DE交直线BC于点F . 请直接写出线段FC的长.20.
(1)、【问题探究】如图1,正方形ABCD中,点F、G分别在边BC、CD上,且AF⊥BG于点P , 求证:AF=BG;(2)、【知识迁移】如图2,矩形ABCD中,AB=4,BC=8,点E、F、G、H分别在边AB、BC、CD、AD上,且EG⊥FH于点P . 若EG•HF=48,求HF的长;(3)、【拓展应用】如图3,在菱形ABCD中,∠ABC=60°,AB=6,点E在直线AB上,BE=4,AF⊥DE交直线BC于点F . 请直接写出线段FC的长.20.【活动探究】在数学课上,老师出示了一个问题:如图1,在菱形ABCD中, , 点E,F分别是BC,CD边上一点,若 , 试猜想的形状,不用证明.
【尝试实践】小美受此启发,她尝试将“”改为“”,通过测量验证发现猜想仍然成立,并进一步思考证法:如图2,过点作 , 求证
请你按照小美的思路进一步思考,并解答这个问题.
【拓展应用】小玲在老师问题上进一步改编:如图3,过作于点 , 当EF的中点经过CG时,请直接写出EF的长度.
 21. 定义:把斜边重合,且直角顶点不重合
21. 定义:把斜边重合,且直角顶点不重合 两个直角三角形叫做共边直角三角形.
两个直角三角形叫做共边直角三角形. (1)、概念理解:如图1,在和中, , 说明和是共边直角三角形.(2)、问题探究:如图2,和是共边直角三角形,E、F分别是、的中点,连结 , 求证 .(3)、拓展延伸:如图3,和是共边直角三角形,且 , 连结 , 求证:平分 .22. 综合与探究
(1)、概念理解:如图1,在和中, , 说明和是共边直角三角形.(2)、问题探究:如图2,和是共边直角三角形,E、F分别是、的中点,连结 , 求证 .(3)、拓展延伸:如图3,和是共边直角三角形,且 , 连结 , 求证:平分 .22. 综合与探究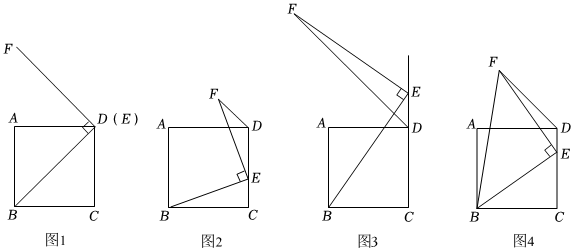
问题情境:数学课上,老师引导同学们以“正方形中线段的旋转”为主题开展数学活动已知正方形中, , 点是射线上一点不与点重合 , 连接将绕点顺时针旋转得到 , 连接 .
(1)、特例分析:如图 , 当点与点重合时,求的度数;
(2)、深入探究:当点不与点重合时,中的结论是否仍然成立?若成立,请在图与图中选择一种情况进行证明:若不成立,请说明理由;
(3)、问题解决:如图 , 当点在线段上,且时,请直接写出线段的长.23. 定义:长宽比为(n为正整数)的矩形称为矩形.下面,我们通过折叠的方式折出一个矩形,如图①所示.操作1:将正方形沿过点的直线折叠,使折叠后的点落在对角线上的点处,折痕为 .
操作2:将沿过点的直线折叠,使点 , 点分别落在边 , 上,折痕为 .
则四边形为矩形.
证明:设正方形的边长为1,则 .
由折叠性质可知 , , 则四边形为矩形,
∴ , ∴ .
∴ , 即 , ∴ , ∴ ,
∴四边形为矩形.

阅读以上内容,回答下列问题:
(1)、在图①中,所有与相等的线段是、 , 的值是;(2)、已知四边形为矩形,模仿上述操作,得到四边形 , 如图②,求证:四边形为矩形;(3)、将图②中的矩形沿用(2)中的方式操作3次后,得到一个“矩形”,则的值是 .24. 【提出问题】如图 , 在等腰中, , 分别以 , 为边作等边和等边 , 与相交于点 , 连接 .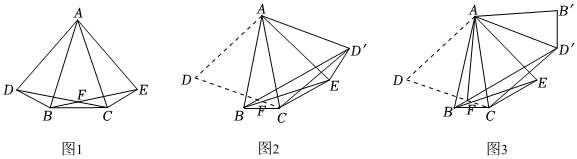 (1)、【初步探究】如图 , 连接 , 求证:≌ .(2)、【深入探究】如图 , 将沿翻折得到 , 连接 , , 类比的探究方法发现:
(1)、【初步探究】如图 , 连接 , 求证:≌ .(2)、【深入探究】如图 , 将沿翻折得到 , 连接 , , 类比的探究方法发现:
结论:_▲_≌;
结论: .
请证明结论 .(3)、如图、在的情况下将线段沿翻折得到线段 , 连接 , , 试判断线段与的位置关系.