2024年中考数学精选压轴题之平行四边形与特殊的平行四边形
试卷更新日期:2024-05-10 类型:三轮冲刺
一、选择题(每题3分,共36分)
-
1. 如图,在边长为2的等边三角形ABC的外侧作正方形ABED,过点D作DF⊥BC,垂足为F,则DF的长为( )
 A、2+2 B、5- C、3- D、+12. 如图,在四边形ABCD中,∠A=∠B=90°,AD=10cm,BC=8cm,点P从点D出发,以1cm/s的速度向点A运动,点M从点B同时出发,以相同的速度向点C运动,当其中一个动点到达端点时,两个动点同时停止运动.设点P的运动时间为t(单位:s),下列结论正确的是 ( )
A、2+2 B、5- C、3- D、+12. 如图,在四边形ABCD中,∠A=∠B=90°,AD=10cm,BC=8cm,点P从点D出发,以1cm/s的速度向点A运动,点M从点B同时出发,以相同的速度向点C运动,当其中一个动点到达端点时,两个动点同时停止运动.设点P的运动时间为t(单位:s),下列结论正确的是 ( ) A、当 t=4s 时,四边形 ABMP 为矩形 B、当 t=5s 时,四边形 CDPM 为平行四边形 C、当 CD=PM 时,t=4s D、当 CD=PM 时,t=4s 或6s3. 如图,直角三角形顶点在矩形的对角线上运动,连接 . , , , 则的最小值为( ).
A、当 t=4s 时,四边形 ABMP 为矩形 B、当 t=5s 时,四边形 CDPM 为平行四边形 C、当 CD=PM 时,t=4s D、当 CD=PM 时,t=4s 或6s3. 如图,直角三角形顶点在矩形的对角线上运动,连接 . , , , 则的最小值为( ). A、 B、 C、 D、4. 如图,在中, , 分别以、为边向外作正方形、 , 连结并延长交于点H , 连结 . 若 , 则的值为( )
A、 B、 C、 D、4. 如图,在中, , 分别以、为边向外作正方形、 , 连结并延长交于点H , 连结 . 若 , 则的值为( ) A、 B、 C、 D、5. 如图,在正方形中,是等边三角形, , 的延长线分别交于点 , , 连接 , ;与相交于点 . 给出下列结论:①;②;③;④;⑤ . 其中正确的结论有( )
A、 B、 C、 D、5. 如图,在正方形中,是等边三角形, , 的延长线分别交于点 , , 连接 , ;与相交于点 . 给出下列结论:①;②;③;④;⑤ . 其中正确的结论有( ) A、1个 B、2个 C、3个 D、4个6. 如图,在平面直角坐标系中,直线分别与轴、轴交于点、 , 在中从左向右依次作正方形、、 , 点、、在轴上,点在轴上,点、、在直线上;再将每个正方形分割成四个全等的直角三角形和一个小正方形,其中每个小正方形的边都与坐标轴平行,从左至右的小正方形阴影部分的面积分别记为、、 , 则可表示为
A、1个 B、2个 C、3个 D、4个6. 如图,在平面直角坐标系中,直线分别与轴、轴交于点、 , 在中从左向右依次作正方形、、 , 点、、在轴上,点在轴上,点、、在直线上;再将每个正方形分割成四个全等的直角三角形和一个小正方形,其中每个小正方形的边都与坐标轴平行,从左至右的小正方形阴影部分的面积分别记为、、 , 则可表示为 A、 B、 C、 D、7. 如图,正方形ABCD的对角线相交于O点,BE平分∠ABO交AO于E点,CF⊥BE于F点,交BO于G点,连接EG、OF,下列四个结论:①CE=CB;②AE=OE;③OF=CG,其中正确的结论只有( )
A、 B、 C、 D、7. 如图,正方形ABCD的对角线相交于O点,BE平分∠ABO交AO于E点,CF⊥BE于F点,交BO于G点,连接EG、OF,下列四个结论:①CE=CB;②AE=OE;③OF=CG,其中正确的结论只有( )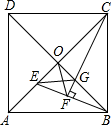 A、①②③ B、②③ C、①③ D、①②8. 如图,在△ABC中,∠ACB=90°,以AC,BC和AB为边向上作正方形ACEF和正方形BCMI和正方形ABGF,点G落在MI上,若AC+BC=7,空白部分面积为16,则图中阴影部分的面积是( )
A、①②③ B、②③ C、①③ D、①②8. 如图,在△ABC中,∠ACB=90°,以AC,BC和AB为边向上作正方形ACEF和正方形BCMI和正方形ABGF,点G落在MI上,若AC+BC=7,空白部分面积为16,则图中阴影部分的面积是( )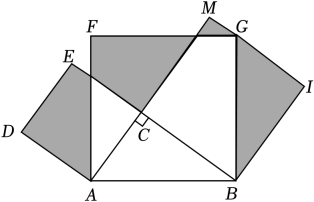 A、16 B、15 C、. D、9. 如图,正方形ABCD的边长为4,点E,F分别在边DC,BC上,且BF=CE,AE平分∠CAD,连接DF,分别交AE,AC于点G,M.P是线段AG上的一个动点,过点P作PN⊥AC,垂足为N,连接PM.有下列四个结论:
A、16 B、15 C、. D、9. 如图,正方形ABCD的边长为4,点E,F分别在边DC,BC上,且BF=CE,AE平分∠CAD,连接DF,分别交AE,AC于点G,M.P是线段AG上的一个动点,过点P作PN⊥AC,垂足为N,连接PM.有下列四个结论:①AE垂直平分DM;②PM+PN的最小值为3;③CF2=GE•AE;④S△ADM=6 .
其中正确的是( )
 A、①② B、②③④ C、①③④ D、①③10. 如图,在矩形中, , 点分别在边上,且与关于直线对称.点在边上,分别与交于两点.若 , , 则( )
A、①② B、②③④ C、①③④ D、①③10. 如图,在矩形中, , 点分别在边上,且与关于直线对称.点在边上,分别与交于两点.若 , , 则( )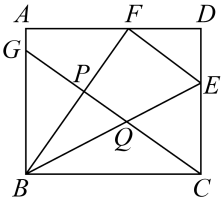 A、 B、 C、 D、11. 如图,把菱形向平移至的位置,作 , 垂足为与相交于点的延长线交于点 , 连接 , 则下列结论:①;②;③;④ , 则正确的结论有( )个
A、 B、 C、 D、11. 如图,把菱形向平移至的位置,作 , 垂足为与相交于点的延长线交于点 , 连接 , 则下列结论:①;②;③;④ , 则正确的结论有( )个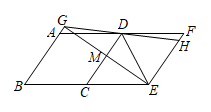 A、1 B、2 C、3 D、412. 如图,边长为的正方形ABCD , 对角线AC , BD相交于O , E为BC边上一动点(不与B , C重合),OF⊥OE交CD于F , G为EF中点.给出如下四个结论:①∠OEF=45°;②点E在运动过程中,△OEF面积不变化;③△CEF周长的最小值为;④点E在运动过程中,OG与CG始终相等,其中正确的结论是( )
A、1 B、2 C、3 D、412. 如图,边长为的正方形ABCD , 对角线AC , BD相交于O , E为BC边上一动点(不与B , C重合),OF⊥OE交CD于F , G为EF中点.给出如下四个结论:①∠OEF=45°;②点E在运动过程中,△OEF面积不变化;③△CEF周长的最小值为;④点E在运动过程中,OG与CG始终相等,其中正确的结论是( ) A、①③ B、②③ C、①④ D、①③④
A、①③ B、②③ C、①④ D、①③④二、填空题(每题3分,共18分)
-
13. 如图,在矩形中,是的中点,连接 , 将沿着翻折得到 , 交于点 , 延长 , 相交于点 , 若 , , 则 .
 14. 如图,正方形中,M、N分别是、边上的点,将四边形沿直线翻折,使得点A、B分别落在点、处,且点恰好为线段的中点,交于点G , 作于点P , 交于点Q . 若 , 则 .
14. 如图,正方形中,M、N分别是、边上的点,将四边形沿直线翻折,使得点A、B分别落在点、处,且点恰好为线段的中点,交于点G , 作于点P , 交于点Q . 若 , 则 . 15. 在菱形中, , 点P是对角线上一动点,点Q是边上一动点,与始终相等,连结 , 交点为E , 连结 , 则的最小值是 .
15. 在菱形中, , 点P是对角线上一动点,点Q是边上一动点,与始终相等,连结 , 交点为E , 连结 , 则的最小值是 . 16. 如图,在长方形中,为等腰△,且 , 点在线段上,点在线段上,若 , 则 .
16. 如图,在长方形中,为等腰△,且 , 点在线段上,点在线段上,若 , 则 . 17. 如图,在菱形中,E、F分别是 , 边上的中点,为 上一点,若 , , 则的长为
17. 如图,在菱形中,E、F分别是 , 边上的中点,为 上一点,若 , , 则的长为 18. 如图,菱形中, , , , 垂足为 , 点在菱形的边上,若 , 则的长为 .
18. 如图,菱形中, , , , 垂足为 , 点在菱形的边上,若 , 则的长为 .
三、解答题(共6题,共46分)
-
19. 如图,在平行四边形中,点E在边上,且 , F为线段上一点,且.
 (1)、求证:;(2)、求证:;(3)、若 , , , 连结 , 求的长度.20. 如图①,在平行四边形ABCD中, , , , 点E为BC中点,动点P从点E出发,沿折线以每秒个单位长度的速度运动.作 , EQ交边AD或边DC于点Q , 连接PQ . 当点P与点A重合时,点P停止运动.设点P的运动时间为t秒.()
(1)、求证:;(2)、求证:;(3)、若 , , , 连结 , 求的长度.20. 如图①,在平行四边形ABCD中, , , , 点E为BC中点,动点P从点E出发,沿折线以每秒个单位长度的速度运动.作 , EQ交边AD或边DC于点Q , 连接PQ . 当点P与点A重合时,点P停止运动.设点P的运动时间为t秒.() (1)、当P在AB上运动时,用含t的式子表示出线段BP的长;(2)、当Q落在CD的中点时,求t的值;(3)、若Q不与顶点重合,当Q落在平行四边形ABCD的某一内角平分线上时,求的值;(4)、作点E关于直线PQ的对称点F , 连接PF、QF , 当四边形EPFQ和平行四边形ABCD重叠部分图形为轴对称四边形时,直接写出t的取值范围.21. 已知和都是等腰三角形,且 , , 若点D在边上运动时,总保持 , 连接与交于点F .
(1)、当P在AB上运动时,用含t的式子表示出线段BP的长;(2)、当Q落在CD的中点时,求t的值;(3)、若Q不与顶点重合,当Q落在平行四边形ABCD的某一内角平分线上时,求的值;(4)、作点E关于直线PQ的对称点F , 连接PF、QF , 当四边形EPFQ和平行四边形ABCD重叠部分图形为轴对称四边形时,直接写出t的取值范围.21. 已知和都是等腰三角形,且 , , 若点D在边上运动时,总保持 , 连接与交于点F . (1)、①如图1,当点D为边中点时,则的值为 ▲ ;
(1)、①如图1,当点D为边中点时,则的值为 ▲ ;②如图2,当点D不为边中点时,求证:;
(2)、如图3,当点D在边上运动中恰好使得时,若 , , 求的长.22. 如图,在矩形中, , , 点从点出发沿以的速度向点移动;同时,点从点出发沿以的速度向点移动,当其中一点到达终点运动即停止.设运动时间为秒. (1)、在运动过程中,的长度能否为?若能,求出的值,若不能,请说明理由;(2)、在运动过程中,的面积能否为?若能,求出的值,若不能,请说明理由;(3)、取的中点 , 运动过程中,当时,求的值;
(1)、在运动过程中,的长度能否为?若能,求出的值,若不能,请说明理由;(2)、在运动过程中,的面积能否为?若能,求出的值,若不能,请说明理由;(3)、取的中点 , 运动过程中,当时,求的值;