2024年中考数学精选压轴题之二次函数(一)
试卷更新日期:2024-05-10 类型:三轮冲刺
一、选择题(每题3分,共36分)
-
1. 已知二次函数的对称轴为 , 当时,y的取值范围是 . 则的值为( )A、或 B、或 C、 D、2. 抛物线与轴的一个交点为 , 与轴交于点 , 点是抛物线的顶点,对称轴为直线 , 其部分图象如图所示,则以下个结论:; , 是抛物线上的两个点,若 , 且 , 则;在轴上有一动点 , 当的值最小时,则点的坐标为;若关于的方程无实数根,则的取值范围是其中正确的结论有( )
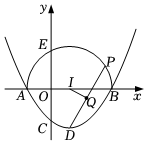
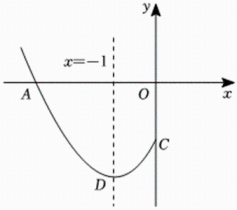 A、个 B、个 C、个 D、个3. 如图,抛物线与轴交于点 , , 与轴交于点 , 顶点为 , 以为直径在轴上方画半圆交轴于点 , 圆心为 , 是半圆上一动点,连接 , 点为的中点.下列四种说法:
A、个 B、个 C、个 D、个3. 如图,抛物线与轴交于点 , , 与轴交于点 , 顶点为 , 以为直径在轴上方画半圆交轴于点 , 圆心为 , 是半圆上一动点,连接 , 点为的中点.下列四种说法:点在上;
;
当点沿半圆从点运动至点时,点运动的路径长为;
线段的长可以是 .
其中正确说法的个数为( )
 A、个 B、个 C、个 D、个4. 如图,在中, , 点为中点,点为线段上的动点,连接 , 设 , 则与之间的函数关系图像大致为( )
A、个 B、个 C、个 D、个4. 如图,在中, , 点为中点,点为线段上的动点,连接 , 设 , 则与之间的函数关系图像大致为( ) A、
A、 B、
B、 C、
C、 D、
D、 5. 如图,抛物线y=x2﹣8x+15与x轴交于A、B两点,对称轴与x轴交于点C , 点D(0,﹣2),点E(0,﹣6),点P是平面内一动点,且满足∠DPE=90°,M是线段PB的中点,连接CM . 则线段CM的最大值是( )
5. 如图,抛物线y=x2﹣8x+15与x轴交于A、B两点,对称轴与x轴交于点C , 点D(0,﹣2),点E(0,﹣6),点P是平面内一动点,且满足∠DPE=90°,M是线段PB的中点,连接CM . 则线段CM的最大值是( ) A、3 B、 C、 D、56. 已知函数f(x)=x2+2x , g(x)=2x2+6x+n2+3,当x=1时,f(1)=12+2×1=3,g(1)=2+6+n2+3=n2+11.则以下结论正确的有( )
A、3 B、 C、 D、56. 已知函数f(x)=x2+2x , g(x)=2x2+6x+n2+3,当x=1时,f(1)=12+2×1=3,g(1)=2+6+n2+3=n2+11.则以下结论正确的有( )①若函数g(x)的顶点在x轴上,则;
②无论x取何值,总有g(x)>f(x);
③若﹣1≤x≤1时,g(x)+f(x)的最小值为7,则n=±3;
④当n=1时,令 , 则h(1)•h(2)…h(2023)=2024.
A、1个 B、2个 C、3个 D、4个7. 如图,经过的直线与抛物线交于B , C两点,且 , 则直线的解析式是( ) A、 B、 C、 D、8. 如图1,一个移动喷灌架喷射出的水流可以近似地看成抛物线.图2是喷灌架为一坡地草坪喷水的平面示意图,喷水头的高度(喷水头距喷灌架底部的距离)是1米.当喷射出的水流距离喷水头20米时,达到最大高度11米,现将喷灌架置于坡度为1∶10的坡地底部点O处,草坡上距离О的水平距离为30米处有一棵高度约为2.3米的石榴树AB,因为刚刚被喷洒了农药,近期不能被喷灌.下列说法正确的是( )
A、 B、 C、 D、8. 如图1,一个移动喷灌架喷射出的水流可以近似地看成抛物线.图2是喷灌架为一坡地草坪喷水的平面示意图,喷水头的高度(喷水头距喷灌架底部的距离)是1米.当喷射出的水流距离喷水头20米时,达到最大高度11米,现将喷灌架置于坡度为1∶10的坡地底部点O处,草坡上距离О的水平距离为30米处有一棵高度约为2.3米的石榴树AB,因为刚刚被喷洒了农药,近期不能被喷灌.下列说法正确的是( ) A、水流运行轨迹满足函数 B、水流喷射的最远水平距离是40米 C、喷射出的水流与坡面OA之间的最大铅直高度是9.1米 D、若将喷灌架向后移动7米,可以避开对这棵石榴树的喷灌9. 对于每个非零自然数 , 抛物线与轴交于、两点,以表示这两点间的距离,则的值是( )A、 B、 C、 D、10. 一个水杯竖直放置时的纵向截面如图1所示,其左右轮廓线AC,BD都是同一条抛物线的一部分,AB,CD都与水面桌面平行,已知水杯底部AB宽为4cm,水杯高度为12cm,当水面高度为6cm时,水面宽度为2cm.如图2先把水杯盛满水,再将水杯绕A点倾斜倒出部分水,如图3,当倾斜角∠BAF=30°时,杯中水面CE平行水平桌面AF.则此时水面CE的值是( )
A、水流运行轨迹满足函数 B、水流喷射的最远水平距离是40米 C、喷射出的水流与坡面OA之间的最大铅直高度是9.1米 D、若将喷灌架向后移动7米,可以避开对这棵石榴树的喷灌9. 对于每个非零自然数 , 抛物线与轴交于、两点,以表示这两点间的距离,则的值是( )A、 B、 C、 D、10. 一个水杯竖直放置时的纵向截面如图1所示,其左右轮廓线AC,BD都是同一条抛物线的一部分,AB,CD都与水面桌面平行,已知水杯底部AB宽为4cm,水杯高度为12cm,当水面高度为6cm时,水面宽度为2cm.如图2先把水杯盛满水,再将水杯绕A点倾斜倒出部分水,如图3,当倾斜角∠BAF=30°时,杯中水面CE平行水平桌面AF.则此时水面CE的值是( ) A、 B、12cm C、 D、14cm11. 将抛物线位于轴左侧的部分沿轴翻折,其余部分不变,翻折得到的图象和原来不变的部分构成一个新图象,若直线与新图象有且只有2个公共点,则的取值范围是( )A、 B、 C、或 D、或12. 如图,已知二次函数的图象与x轴交于A、B两点(点A在点B的左侧),与轴交于点C,P为该二次函数在第一象限内的一点,连接AP,交BC于点K,则的最小值为( )
A、 B、12cm C、 D、14cm11. 将抛物线位于轴左侧的部分沿轴翻折,其余部分不变,翻折得到的图象和原来不变的部分构成一个新图象,若直线与新图象有且只有2个公共点,则的取值范围是( )A、 B、 C、或 D、或12. 如图,已知二次函数的图象与x轴交于A、B两点(点A在点B的左侧),与轴交于点C,P为该二次函数在第一象限内的一点,连接AP,交BC于点K,则的最小值为( ) A、 B、2 C、 D、
A、 B、2 C、 D、二、填空题(每题3分,共18分)
-
13. 抛物线与轴相交于不同两点、 , 若存在整数及整数 , 使得和同时成立,则 .14. 若关于x的方程恰有三个根,则t的值为.15. 如图,在平面直角坐标系中,二次函数y=x2+2x-3的图象与坐标轴相交于A , B , C三点,连接AC , BC . 已知点E坐标为 , 点D在线段AC上,且 . 则四边形BCDE面积的大小为 .
 16. 图1是一个瓷碗,图 2 是其截面图,碗体 DEC 呈抛物线状(碗体厚度不计),碗口宽CD=12cm,此时面汤最大深度EG=8cm.
16. 图1是一个瓷碗,图 2 是其截面图,碗体 DEC 呈抛物线状(碗体厚度不计),碗口宽CD=12cm,此时面汤最大深度EG=8cm. (1)、当面汤的深度ET为4cm时,汤面的直径PQ长为;(2)、如图3,把瓷碗绕点B缓缓倾斜倒出部分面汤,当∠ABM=45°时停止,此时碗中液面宽度CH= .17. 如图,抛物线 过点A(1,0),B(3,0),与y轴相交于点C.若点P为线段OC上的动点,连结BP,过点C作CN垂直于直线BP,垂足为N,当点P从点O运动到点C时,点N运动路径的长为
(1)、当面汤的深度ET为4cm时,汤面的直径PQ长为;(2)、如图3,把瓷碗绕点B缓缓倾斜倒出部分面汤,当∠ABM=45°时停止,此时碗中液面宽度CH= .17. 如图,抛物线 过点A(1,0),B(3,0),与y轴相交于点C.若点P为线段OC上的动点,连结BP,过点C作CN垂直于直线BP,垂足为N,当点P从点O运动到点C时,点N运动路径的长为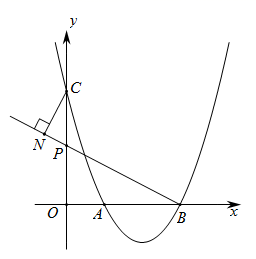
三、解答题(共6题,共46分)
-
18. 如图,在平面直角坐标系中,抛物线与轴交于两点 , , 与轴交于点 .
 (1)、求此抛物线的解析式;(2)、已知抛物线上有一点 , 其中 , 若 , 求的值;(3)、若点 , 分别是线段 , 上的动点,且 , 求的最小值.19. 如图,灌溉车为绿化带浇水,喷水口离地竖直高度为 . 可以把灌溉车喷出水的上、下边缘抽象为平面直角坐标系中两条抛物线的部分图象;把绿化带横截面抽象为矩形 , 其水平宽度 , 竖直高度 . 下边缘抛物线是由上边缘抛物线向左平移得到,上边抛物线最高点离喷水口的水平距离为、高出喷水口 , 灌溉车到绿化带的距离为(单位:)
(1)、求此抛物线的解析式;(2)、已知抛物线上有一点 , 其中 , 若 , 求的值;(3)、若点 , 分别是线段 , 上的动点,且 , 求的最小值.19. 如图,灌溉车为绿化带浇水,喷水口离地竖直高度为 . 可以把灌溉车喷出水的上、下边缘抽象为平面直角坐标系中两条抛物线的部分图象;把绿化带横截面抽象为矩形 , 其水平宽度 , 竖直高度 . 下边缘抛物线是由上边缘抛物线向左平移得到,上边抛物线最高点离喷水口的水平距离为、高出喷水口 , 灌溉车到绿化带的距离为(单位:) (1)、求上边缘抛物线的函数解析式,并求喷出水的最大射程;(2)、求下边缘抛物线与x轴的正半轴交点的坐标;(3)、要使灌溉车行驶时喷出的水能浇灌到整个绿化带,直接写出的取值范围20. 如图1,已知二次函数图象与轴交点为 , 其顶点为 .
(1)、求上边缘抛物线的函数解析式,并求喷出水的最大射程;(2)、求下边缘抛物线与x轴的正半轴交点的坐标;(3)、要使灌溉车行驶时喷出的水能浇灌到整个绿化带,直接写出的取值范围20. 如图1,已知二次函数图象与轴交点为 , 其顶点为 .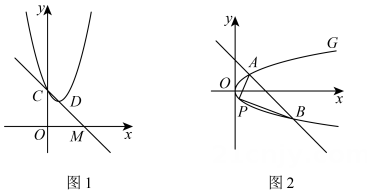 (1)、求二次函数的表达式;(2)、将二次函数图象平移,使其顶点与原点重合,然后将其图象绕点顺时针旋转得到抛物线 , 如图,直线与交于 , 两点,为上位于直线左侧一点,求面积最大值,及此时点的坐标.21. 如图1,抛物线y=﹣x2+bx+c过点A(﹣1,0),点B(3,0),与y轴交于点C . 在x轴上有一动点E(m , 0)(0<m<3),过点E作直线ME⊥x轴,交抛物线于点M .
(1)、求二次函数的表达式;(2)、将二次函数图象平移,使其顶点与原点重合,然后将其图象绕点顺时针旋转得到抛物线 , 如图,直线与交于 , 两点,为上位于直线左侧一点,求面积最大值,及此时点的坐标.21. 如图1,抛物线y=﹣x2+bx+c过点A(﹣1,0),点B(3,0),与y轴交于点C . 在x轴上有一动点E(m , 0)(0<m<3),过点E作直线ME⊥x轴,交抛物线于点M . (1)、求抛物线的解析式;(2)、当m=1时,点D是直线ME上的点且在第一象限内,若△ACD是以CA为斜边的直角三角形,求点D的坐标;(3)、如图2,连接BC , BC与ME交于点F , 连接AF , △ACF和△BFM的面积分别为S1和S2 , 当S1=4S2时,求点E坐标.22. 如图所示,在平面直角坐标系中,抛物线y=ax2+bx+3经过点 A(-1,0),B(3,0),与 y轴交于点C,直线 y=x+2与y轴交于点D,交抛物线于E,F两点,点P为线段EF上一个动点(与E,F不重合),PQ∥y轴与抛物线交于点Q.
(1)、求抛物线的解析式;(2)、当m=1时,点D是直线ME上的点且在第一象限内,若△ACD是以CA为斜边的直角三角形,求点D的坐标;(3)、如图2,连接BC , BC与ME交于点F , 连接AF , △ACF和△BFM的面积分别为S1和S2 , 当S1=4S2时,求点E坐标.22. 如图所示,在平面直角坐标系中,抛物线y=ax2+bx+3经过点 A(-1,0),B(3,0),与 y轴交于点C,直线 y=x+2与y轴交于点D,交抛物线于E,F两点,点P为线段EF上一个动点(与E,F不重合),PQ∥y轴与抛物线交于点Q. (1)、求抛物线的解析式.(2)、当P在什么位置时,四边形PDCQ为平行四边形?求出此时点P的坐标.23. 在平面直角坐标系中,二次函数的图象与轴交于、两点,与轴交于点 , 过点 , 且顶点的坐标为.
(1)、求抛物线的解析式.(2)、当P在什么位置时,四边形PDCQ为平行四边形?求出此时点P的坐标.23. 在平面直角坐标系中,二次函数的图象与轴交于、两点,与轴交于点 , 过点 , 且顶点的坐标为. (1)、求二次函数的解析式;(2)、如图1,若点是二次函数图象上的点,且在直线的上方,连接 , .求面积的最大值及此时点的坐标;(3)、如图2,设点是抛物线对称轴上的一点,连接 , 将线段绕点逆时针旋转 , 点的对应点为 , 连接交抛物线于点 , 求点的坐标.
(1)、求二次函数的解析式;(2)、如图1,若点是二次函数图象上的点,且在直线的上方,连接 , .求面积的最大值及此时点的坐标;(3)、如图2,设点是抛物线对称轴上的一点,连接 , 将线段绕点逆时针旋转 , 点的对应点为 , 连接交抛物线于点 , 求点的坐标.