2024年中考数学精选压轴题之一次函数综合
试卷更新日期:2024-05-10 类型:三轮冲刺
一、选择题(每题3分,共36分)
-
1. 一次函数y=(m-2)x+2-m和y=x+m在同一平面直角坐标系中的图象可能是( )A、
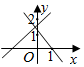 B、
B、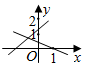 C、
C、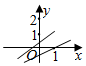 D、
D、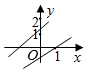 2. 如图所示,直线y=x+3分别与x轴、y轴交于点A、B,若∠ABC=45°,则直线BC的函数表达式为( )
2. 如图所示,直线y=x+3分别与x轴、y轴交于点A、B,若∠ABC=45°,则直线BC的函数表达式为( )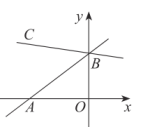 A、y=x+3 B、y=x+3 C、y=x+3 D、y=x+33. 若是一次函数图象上的不同的两点,记 , 则当时,的取值范围是( )A、 B、 C、 D、4. 如图,已知点P(6,2),点M , N分别是直线l1:y=x和直线l2:上的动点,连接PM , MN . 则PM+MN的最小值为( )
A、y=x+3 B、y=x+3 C、y=x+3 D、y=x+33. 若是一次函数图象上的不同的两点,记 , 则当时,的取值范围是( )A、 B、 C、 D、4. 如图,已知点P(6,2),点M , N分别是直线l1:y=x和直线l2:上的动点,连接PM , MN . 则PM+MN的最小值为( ) A、2 B、 C、 D、5. 甲、乙两车从A城出发匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离y(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示.则下列结论:
A、2 B、 C、 D、5. 甲、乙两车从A城出发匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离y(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示.则下列结论:
①A , B两城相距300千米;
②乙车比甲车晚出发1小时,却早到1小时;
③乙车出发后1.5小时追上甲车;
④当甲、乙两车相距50千米时,t=或 .
其中正确的结论有( )
A、1个 B、2个 C、3个 D、4个6. 如图,正方形的边长为 , 点和点在轴正半轴上,点、在第一象限,一次函数的图象交、分别于、 . 若与的面积比为 , 则的值为( )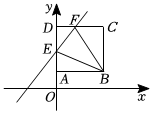 A、 B、 C、 D、7. 一个有进水管与出水管的容器,从某时刻开始的内只进水不出水,在随后的内既进水又出水,之后只出水不进水,每分的进水量和出水量是两个常数,容器内的水量y(单位:)与时间x(单位:)之间的关系如图.则下列说法正确的是( )
A、 B、 C、 D、7. 一个有进水管与出水管的容器,从某时刻开始的内只进水不出水,在随后的内既进水又出水,之后只出水不进水,每分的进水量和出水量是两个常数,容器内的水量y(单位:)与时间x(单位:)之间的关系如图.则下列说法正确的是( ) A、进水管每分钟的进水量为 B、当时, C、出水管每分钟的出水量为 D、水量为的时间为或8. 已知、两地是一条直路,甲车从地到地,乙车从地到地,两车同时出发,乙先到达目的地,两车之间的距离()与运动时间()的函数关系大致如图所示,下列说法错误的是( )
A、进水管每分钟的进水量为 B、当时, C、出水管每分钟的出水量为 D、水量为的时间为或8. 已知、两地是一条直路,甲车从地到地,乙车从地到地,两车同时出发,乙先到达目的地,两车之间的距离()与运动时间()的函数关系大致如图所示,下列说法错误的是( )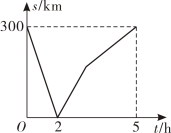 A、两车出发后相遇 B、甲车的速度为/ C、乙的速度为/ D、乙车比甲车提前到达目的地9. 如图1,四边形中, , , 点从点出发,以每秒个单位长度的速度,沿路线A-B-C-D运动.设点的运动时间为 , 的面积为 , 当运动到的中点时,的面积为( )
A、两车出发后相遇 B、甲车的速度为/ C、乙的速度为/ D、乙车比甲车提前到达目的地9. 如图1,四边形中, , , 点从点出发,以每秒个单位长度的速度,沿路线A-B-C-D运动.设点的运动时间为 , 的面积为 , 当运动到的中点时,的面积为( ) A、 B、 C、 D、10. 一次函数( , k、b是常数)与( , m是常数)的图像交于点 , 下列结论正确的序号是( )
A、 B、 C、 D、10. 一次函数( , k、b是常数)与( , m是常数)的图像交于点 , 下列结论正确的序号是( )①关于的方程的解为;
②一次函数()图像上任意不同两点和满足:;
③若(),则;
④若 , 且 , 则当时, .
A、②③④ B、①②④ C、①②③ D、①②③④11. 如图,已知直线与轴交于点A,点与点A关于轴对称.是直线上的动点,将绕点顺时针旋转得 . 连接 , 则线段的最小值为( ).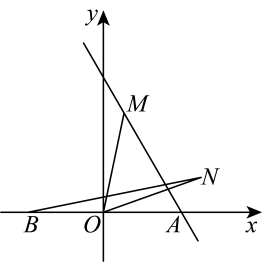 A、3 B、 C、 D、12. 为培养同学们的创新精神,某校举办校园科技节活动,八年级同学进行了机器人行走性能试验.在试验场地有A,B,C三点顺次在同一笔直的赛道上,甲、乙两机器人分别从A,B两点同时同向出发,历时8分钟同时到达C点,乙机器人始终以60米/分的速度行走,如图是甲、乙两机器人之间的距离y(米)与它们的行走时间x(分钟)之间的函数图象,若前3.5分钟甲机器人的速度不变,则出发( )分钟后两机器人最后一次相距6米.
A、3 B、 C、 D、12. 为培养同学们的创新精神,某校举办校园科技节活动,八年级同学进行了机器人行走性能试验.在试验场地有A,B,C三点顺次在同一笔直的赛道上,甲、乙两机器人分别从A,B两点同时同向出发,历时8分钟同时到达C点,乙机器人始终以60米/分的速度行走,如图是甲、乙两机器人之间的距离y(米)与它们的行走时间x(分钟)之间的函数图象,若前3.5分钟甲机器人的速度不变,则出发( )分钟后两机器人最后一次相距6米. A、6 B、6.4 C、6.8 D、7.2
A、6 B、6.4 C、6.8 D、7.2二、填空题(每题3分,共18分)
-
13. 如图,四条直线 , , , , , 过点作轴交于点 , 再过点作 , 交于点 , 再过点作交y轴于点 , ……,则点的坐标为.
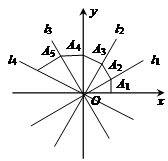 14. 在平面直角坐标系中,点 , 点P的“变换点”Q的坐标定义如下:当时, , 当时, , 线段按上述“变换点”组成新图形,直线与新图形恰好有两个公共点,则k的取值范围 .15. 已知,一次函数的图象与x轴、y轴分别交于点A、点B,在第一象限内有一点P,使得是等腰直角三角形,则点P的横坐标为.16. 在平面直角坐标系中,已知直线l:过点 , 且与坐标轴交于点 , 则当的面积为2,且直线与轴不平行时,直线的表达式为 .
14. 在平面直角坐标系中,点 , 点P的“变换点”Q的坐标定义如下:当时, , 当时, , 线段按上述“变换点”组成新图形,直线与新图形恰好有两个公共点,则k的取值范围 .15. 已知,一次函数的图象与x轴、y轴分别交于点A、点B,在第一象限内有一点P,使得是等腰直角三角形,则点P的横坐标为.16. 在平面直角坐标系中,已知直线l:过点 , 且与坐标轴交于点 , 则当的面积为2,且直线与轴不平行时,直线的表达式为 . 17. 如图,在平面直角坐标系中,直线:;直线l2: , 直线上有一点A , 且点A的纵坐标是 . 在直线的右侧作正方形 , 交直线于点D , 交x轴于点E , 连接交直线于点F , 交x轴于点G , 则下列结论正确的有 . (填序号)
17. 如图,在平面直角坐标系中,直线:;直线l2: , 直线上有一点A , 且点A的纵坐标是 . 在直线的右侧作正方形 , 交直线于点D , 交x轴于点E , 连接交直线于点F , 交x轴于点G , 则下列结论正确的有 . (填序号)①的周长为;
②;
③;
④点P为射线上一动点,的最小值为 .
 18. 如图,在平面直角坐标系中,一次函数的图象分别交、轴于点、 , 将直线绕点按顺时针方向旋转 , 交轴于点 , 则直线的函数表达式是.
18. 如图,在平面直角坐标系中,一次函数的图象分别交、轴于点、 , 将直线绕点按顺时针方向旋转 , 交轴于点 , 则直线的函数表达式是.
三、解答题(共5题,共38分)
-
19. 如图是由小正方形组成的网格,每个边长为1的小正方形的顶点叫做格点.正方形四个顶点都是格点.点E的坐标为 . 仅用无刻度的直尺在给定的网格中完成画图,画图过程线用虚线,结果线用实线表示.
 (1)、在图1中,以为边画;(2)、在图1中,在上画点M , 使得;(3)、在图2中,在上画点G , 使得(4)、直接写出与x轴交点的横坐标;20. 如图,已知直线:与轴,轴交于点 , 点 , 直线经过点 , 与直线交于点 .
(1)、在图1中,以为边画;(2)、在图1中,在上画点M , 使得;(3)、在图2中,在上画点G , 使得(4)、直接写出与x轴交点的横坐标;20. 如图,已知直线:与轴,轴交于点 , 点 , 直线经过点 , 与直线交于点 . (1)、求点的坐标及直线的函数表达式;(2)、求的面积;(3)、点为直线上一动点,若有 , 求点的坐标.21.
(1)、求点的坐标及直线的函数表达式;(2)、求的面积;(3)、点为直线上一动点,若有 , 求点的坐标.21.如图,直线与轴,轴分别交于 , 两点,点坐标为 , 连接 , , 点是线段上的一动点,直线过 , 两点.
 (1)、求的面积;(2)、若点的横坐标为1,直线上是否存在点 , 使点到直线的距离为 , 若存在,求出点的坐标,若不存在,请说明理由;(3)、将沿直线翻折,点的对应点为 , 若为直角三角形,求线段的长.22. 我市莲池区开展了“阳光体育,强身健体”系列活动,小明积极参与,他每周末和哥哥一起练习赛跑.哥哥先让小明跑若干米 , 哥哥追上小明后,小明的速度降为原来的一半,已知他们所跑的路程y(m)与哥哥跑步的时间x(s)之间的函数图象如图.
(1)、求的面积;(2)、若点的横坐标为1,直线上是否存在点 , 使点到直线的距离为 , 若存在,求出点的坐标,若不存在,请说明理由;(3)、将沿直线翻折,点的对应点为 , 若为直角三角形,求线段的长.22. 我市莲池区开展了“阳光体育,强身健体”系列活动,小明积极参与,他每周末和哥哥一起练习赛跑.哥哥先让小明跑若干米 , 哥哥追上小明后,小明的速度降为原来的一半,已知他们所跑的路程y(m)与哥哥跑步的时间x(s)之间的函数图象如图. (1)、哥哥的速度是m/s,哥哥让小明先跑了米,小明后来的速度为m/s.(2)、哥哥跑几秒时,哥哥追上小明?(3)、求哥哥跑几秒时,两人相距10米?23. 如图1,已知在中, , 边在轴上,点在轴上, , 的坐标为 , 点是轴上一个动点,它的坐标是 , , 直线交直线于点 .
(1)、哥哥的速度是m/s,哥哥让小明先跑了米,小明后来的速度为m/s.(2)、哥哥跑几秒时,哥哥追上小明?(3)、求哥哥跑几秒时,两人相距10米?23. 如图1,已知在中, , 边在轴上,点在轴上, , 的坐标为 , 点是轴上一个动点,它的坐标是 , , 直线交直线于点 . (1)、求直线的表达式;(2)、若 , 点为直线上一点,且平分 , 求的坐标;(3)、如图 , 连接 , 以为直角边作等腰直角(、、三点按照逆时针顺序排列),使得 , .
(1)、求直线的表达式;(2)、若 , 点为直线上一点,且平分 , 求的坐标;(3)、如图 , 连接 , 以为直角边作等腰直角(、、三点按照逆时针顺序排列),使得 , .①试说明在点的运动过程中,的面积是否为定值,若是请求出定值,若不是请说明理由;
②点从运动到的过程中,点的运动路径长为 ▲ .
四、实践探究题(共8分)
-
24.
 (1)、【模型建立】如图1,在△ABC中, , 直线ED经过点C , 过点A作AD⊥ED于点D , 过点B作BE⊥ED于点E . 求证: ;(2)、【初步应用】如图2,已知直线:分别交轴于点A、B,将直线绕点A逆时针旋转45°至直线 , 求直线的函数表达式;(3)、【迁移拓展】如图3,直线分别交x、y轴于A、B两点,直线分别交x、y轴于点C、D交直线AB于点E . 若∠BED=45°,请直接写出点C的坐标.
(1)、【模型建立】如图1,在△ABC中, , 直线ED经过点C , 过点A作AD⊥ED于点D , 过点B作BE⊥ED于点E . 求证: ;(2)、【初步应用】如图2,已知直线:分别交轴于点A、B,将直线绕点A逆时针旋转45°至直线 , 求直线的函数表达式;(3)、【迁移拓展】如图3,直线分别交x、y轴于A、B两点,直线分别交x、y轴于点C、D交直线AB于点E . 若∠BED=45°,请直接写出点C的坐标.