2024年江苏省徐州市中考数学仿真模拟卷
试卷更新日期:2024-05-10 类型:中考模拟
一、选择题(本大题共有8小题,在每小题所给出的四个选项中,只有一项符合题意,请将正确选项前的字母代号填涂答题卡相应位置)
-
1. 下列事件属于必然事件的是( )A、打开电视,正在播出系列专题片“航拍中国” B、将一组数据中的每一个数都加上同一个数,这组数据的方差不变 C、一个命题的原命题和它的逆命题都是真命题 D、在数轴上任取一点,则这点表示的数是有理数2. 下列图案中,是轴对称图形但不是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 实数 , 在数轴上的对应点的位置如图所示,下列结论中正确的是( )
3. 实数 , 在数轴上的对应点的位置如图所示,下列结论中正确的是( ) A、 B、 C、 D、4. 若 , 下列计算正确的是( )A、 B、 C、 D、5. 九年级1班30位同学的体育素质测试成绩统计如表所示,其中有两个数据被遮盖
A、 B、 C、 D、4. 若 , 下列计算正确的是( )A、 B、 C、 D、5. 九年级1班30位同学的体育素质测试成绩统计如表所示,其中有两个数据被遮盖成绩
24
25
26
27
28
29
30
人数
▄
▄
2
3
6
7
9
下列关于成绩的统计量中,与被遮盖的数据无关的是( )
A、平均数,方差 B、中位数,方差 C、中位数,众数 D、平均数,众数6. 下列整数中,与 最接近的是( )A、3 B、4 C、5 D、67. 二次函数 经过适当变换之后得到新的二次函数 ,则这个变换为( )A、向上5个单位,向右3个单位 B、向下5个单位,向右3个单位 C、向上5个单位,向左3个单位 D、向下5个单位,向左3个单位8. 如图,该几何体是由一个大圆锥截去上部的小圆锥后剩下的部分.若该几何体上、下两个圆的半径分别为1和2,原大圆锥高的剩余部分为 , 则其侧面展开图的面积为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共有10小题,不需要写出解答过程,请将答案直接填写在答题卡相应位置)
-
9. 三角形的两边长分别为4和5,第三边的长是方程x2-12x+20=0的根,则个三角形的第三条边长为.10. 联合国2022年11月15日宣布,全世界人口已达80亿.将8000000000用科学记数法表示为 .11. 若式子 在实数范围内有意义,则 的取值范围是.12. 正n边形的一个外角等于20°,则n= .13.
若关于
 的一元二次方程有两个不相等的实数根,则k的取值范围是 14. 规定:等腰三角形的顶角与一个底角度数的比值叫做等腰三角形的“雅系特征值”,记作k,若 ,则该等腰三角形的顶角为.15. 如图,AB为⊙O的直径,点P为其半圆上任意一点(不含A、B),点Q为另一半圆上一定点,若∠POA为x°,∠PQB为y°,则y与x的函数关系是.
的一元二次方程有两个不相等的实数根,则k的取值范围是 14. 规定:等腰三角形的顶角与一个底角度数的比值叫做等腰三角形的“雅系特征值”,记作k,若 ,则该等腰三角形的顶角为.15. 如图,AB为⊙O的直径,点P为其半圆上任意一点(不含A、B),点Q为另一半圆上一定点,若∠POA为x°,∠PQB为y°,则y与x的函数关系是. 16. 一个圆锥的侧面展开图是半径为8 cm、圆心角为120°的扇形,则此圆锥底面圆的半径为 .
16. 一个圆锥的侧面展开图是半径为8 cm、圆心角为120°的扇形,则此圆锥底面圆的半径为 .
17. 如图,矩形ABCD的顶点A、B分别在反比例函数与的图象上,点C、D在x轴上,AB、BD分别交y轴于点E、F,则阴影部分的面积为 .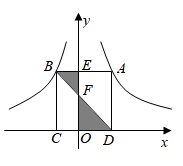 18. 如图,矩形 中, , ,点 是 边上一点,连接 ,把 沿 折叠,使点 落在点 处.当 为直角三角形时,则 的长为.
18. 如图,矩形 中, , ,点 是 边上一点,连接 ,把 沿 折叠,使点 落在点 处.当 为直角三角形时,则 的长为.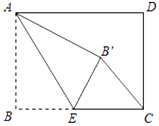
三、解答题(本大题共有10小题,请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤)
-
19. 计算:(1)、 ;(2)、 .20. 解方程组和不等式组:(1)、(2)、21. 3月14日是国际数学日,“数学是打开科学大门的钥匙.”为进一步提高学生学习数学的兴趣,某校开展了一次数学趣味知识竞赛(竞赛成绩为百分制),并随机抽取了50名学生的竞赛成绩(本次竞赛没有满分),经过整理数据得到以下信息:
信息一:50名学生竞赛成绩频数分布直方图如图所示,从左到右依次为第一组到第五组(每组数据含前端点值,不含后端点值).
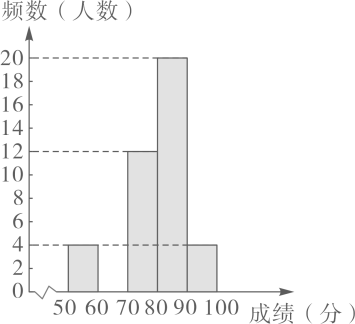
信息二:第三组的成绩(单位:分)为74 71 73 74 79 76 77 76 76 73 72 75
根据信息解答下列问题:
(1)、补全第二组频数分布直方图(直接在图中补全);(2)、第三组竞赛成绩的众数是分,抽取的50名学生竞赛成绩的中位数是分;(3)、若该校共有1500名学生参赛,请估计该校参赛学生成绩不低于80分的约为人.22. 班级团队建设联欢晚会时,在教室悬挂了如图所示的四个灯笼 , , , . 晚会结束后,小明摘下了两个灯笼(剩两个灯笼未摘),他每次随机摘下一个灯笼,且摘之前需先摘下 , 摘之前需先摘下 . (1)、小明第一个摘下的灯笼是灯笼的概率是;(2)、求小明第二个摘下的灯笼是灯笼的概率.23. 某镇准备对一条长3200米道路进行绿化整修,按原计划修了800米后,承包商安排工人每天加班,每天的工作量比原计划提高了20%,共用28天完成了全部任务.(1)、问原计划每天绿化道路多少米?(2)、已知承包商原计划每天支付工人工资5000元,安排工人加班后每天支付给工人的工资增加了40%,则完成此项工程,承包商共需支付工人工资多少元?24. 新冠疫情期间,某网店以100元/件的价格购进一批消毒用紫外线灯,该网店店主结合店铺数据发现,日销量y(件)是售价x(元/件)的一次函数,其售价和日销售量的四组对应值如表:
(1)、小明第一个摘下的灯笼是灯笼的概率是;(2)、求小明第二个摘下的灯笼是灯笼的概率.23. 某镇准备对一条长3200米道路进行绿化整修,按原计划修了800米后,承包商安排工人每天加班,每天的工作量比原计划提高了20%,共用28天完成了全部任务.(1)、问原计划每天绿化道路多少米?(2)、已知承包商原计划每天支付工人工资5000元,安排工人加班后每天支付给工人的工资增加了40%,则完成此项工程,承包商共需支付工人工资多少元?24. 新冠疫情期间,某网店以100元/件的价格购进一批消毒用紫外线灯,该网店店主结合店铺数据发现,日销量y(件)是售价x(元/件)的一次函数,其售价和日销售量的四组对应值如表:售价x(元/件)
150
160
170
180
日销售量y(件)
200
180
160
140
另外,该网店每日的固定成本折算下来为2000元.
注:日销售纯利润=日销售量×(售价﹣进价)﹣每日固定成本
(1)、求y关于x的函数解析式(不要求写出自变量的取值范围);(2)、日销售纯利润为W(元),求出W与x的函数表达式;(3)、当售价定为多少元时,日销售纯利润最大,最大纯利润是多少.25. 如图,某商厦AB建在一个高台上,商厦AB前是一个长度为BC的平台,为方便顾客,商厦修建了坡度为30°的台阶CD,小明在与A,B,C,D同一平面的点E处观测到点A的仰角为57°,已知BC=10米,CD=20米,DE=15米,求商厦AB的高度.(结果保留一位小数,参考数据:sin57°≈0.84,cos57°≈0.54,tan57°≈1.55, ≈1.73) 26. 如果三角形三边的长a、b、c满足 =b,那么我们就把这样的三角形叫做“匀称三角形”,如:三边长分别为1,1,1或3,5,7,…的三角形都是“匀称三角形”.
26. 如果三角形三边的长a、b、c满足 =b,那么我们就把这样的三角形叫做“匀称三角形”,如:三边长分别为1,1,1或3,5,7,…的三角形都是“匀称三角形”. (1)、如图1,已知两条线段的长分别为a、c(a<c).用直尺和圆规作一个最短边、最长边的长分别为a、c的“匀称三角形”(不写作法,保留作图痕迹);(2)、如图2,△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作⊙O的切线交AB延长线于点E,交AC于点F,若 ,判断△AEF是否为“匀称三角形”?请说明理由.27. 如图
(1)、如图1,已知两条线段的长分别为a、c(a<c).用直尺和圆规作一个最短边、最长边的长分别为a、c的“匀称三角形”(不写作法,保留作图痕迹);(2)、如图2,△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作⊙O的切线交AB延长线于点E,交AC于点F,若 ,判断△AEF是否为“匀称三角形”?请说明理由.27. 如图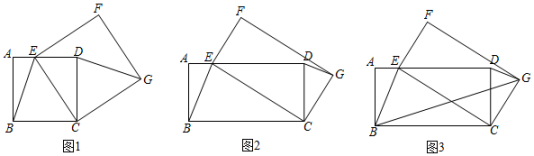 (1)、【问题情境】如图1,四边形ABCD是正方形,点E是AD边上的一个动点,以CE为边在CE的右侧作正方形CEFG,连接DG、BE,则DG与BE的数量关系是;(2)、如图2,四边形ABCD是矩形,AB=2,BC=4,点E是AD边上的一个动点,以CE为边在CE的右侧作矩形CEFG,且CG:CE=1:2,连接DG、BE.判断线段DG与BE有怎样的数量关系和位置关系,并说明理由;(3)、【拓展提升】如图3,在(2)的条件下,连接BG,则2BG+BE的最小值为.28. 已知抛物线y= .
(1)、【问题情境】如图1,四边形ABCD是正方形,点E是AD边上的一个动点,以CE为边在CE的右侧作正方形CEFG,连接DG、BE,则DG与BE的数量关系是;(2)、如图2,四边形ABCD是矩形,AB=2,BC=4,点E是AD边上的一个动点,以CE为边在CE的右侧作矩形CEFG,且CG:CE=1:2,连接DG、BE.判断线段DG与BE有怎样的数量关系和位置关系,并说明理由;(3)、【拓展提升】如图3,在(2)的条件下,连接BG,则2BG+BE的最小值为.28. 已知抛物线y= . (1)、如图1,当c=﹣6时,抛物线分别交x轴于A,B,交y轴于点C.
(1)、如图1,当c=﹣6时,抛物线分别交x轴于A,B,交y轴于点C.①直接写出直线CB的解析式;
②点P在直线BC下方抛物线上,作PD y轴,交线段BC于点D,作PE x轴,交抛物线于另一点E,若PE=PD,求点P的坐标;
(2)、如图2,若抛物线与x轴有唯一公共点F,直线l:y=kx+b(k>0,b>0)与抛物线交于M,N两点(点N在点M右边),直线MG⊥x轴,交直线NF于点G,且点G的纵坐标为-3,求证:直线l过定点.