2024年江苏省泰州市中考数学仿真模拟卷
试卷更新日期:2024-05-10 类型:中考模拟
一、单选题(每题3分,共18分)
-
1. 化简 的结果是( )A、 B、
 C、
C、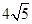 D、
D、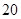 2. 中国古代建筑中的窗格图案美观大方,寓意吉祥,下列绘出的图案中既是轴对称图形又是中心对称图形是( )A、
2. 中国古代建筑中的窗格图案美观大方,寓意吉祥,下列绘出的图案中既是轴对称图形又是中心对称图形是( )A、 B、
B、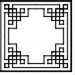 C、
C、 D、
D、 3. 下列运算正确的是( )A、x2•x3=x6 B、(x3)2=x5 C、(xy2)3=x3y6 D、x6÷x3=x24. 投掷硬币m次,正面向上n次,其频率p= ,则下列说法正确的是( )A、p一定等于 B、p一定不等于 C、多投一次,p更接近 D、投掷次数逐步增加,p稳定在 附近5. 函数 的自变量 的取值范围为全体实数,其中 部分的图象如图所示,对于此函数有下列结论:
3. 下列运算正确的是( )A、x2•x3=x6 B、(x3)2=x5 C、(xy2)3=x3y6 D、x6÷x3=x24. 投掷硬币m次,正面向上n次,其频率p= ,则下列说法正确的是( )A、p一定等于 B、p一定不等于 C、多投一次,p更接近 D、投掷次数逐步增加,p稳定在 附近5. 函数 的自变量 的取值范围为全体实数,其中 部分的图象如图所示,对于此函数有下列结论:
①函数图象关于 轴对称;②函数既有最大值,也有最小值;③当 时, 随 的增大而减小;④当 时,关于 的方程 有 个实数根.其中正确的结论个数是( )
A、3 B、2 C、1 D、06. 如图所示,在矩形ABCD中,F是DC上一点,AE平分∠BAF交BC于点E,且DE⊥AF,垂足为点M,BE=3,AE=2 ,则MF的长是( ) A、 B、 C、1 D、
A、 B、 C、1 D、二、填空题(每题3分,共30分)
-
7. 使代数式有意义,则的取值范围为.8. 华为正在研制厚度为0.000 000 005m的芯片.用科学记数法表示0.000 000 005是.9. 如图,E、F分别为矩形ABCD的边AD,BC的中点.若矩形ABCD与矩形EABF相似,AB=6,则AD的长为.
 10. 当时,代数式的值为 .11. 若一个圆锥的底面圆半径为3cm,其侧面展开图的圆心角为120°,则圆锥的母线长是12. 甲、乙两班举行一分钟跳绳比赛,参赛学生每分钟跳绳个数的统计结果如表:
10. 当时,代数式的值为 .11. 若一个圆锥的底面圆半径为3cm,其侧面展开图的圆心角为120°,则圆锥的母线长是12. 甲、乙两班举行一分钟跳绳比赛,参赛学生每分钟跳绳个数的统计结果如表:班级
参加人数
中位数
方差
平均数
甲
45
109
181
110
乙
45
111
108
110
某同学分析上表后得到如下结论:①甲、乙两班学生平均成绩相同;②乙班优秀人数多于甲班优秀人数(每分钟跳绳≥110个为优秀);③甲班成绩的波动比乙班大,则正确结论的序号是.
13. 若x1、x2是一元二次方程x2+2x=3的两根,则x1•x2的值是 .14. 如图,二次函数 的图象与x轴交于 ,对称轴是直线 ,当函数值 时,自变量x的取值范围是 . 15. 如图,在矩形ABCD中,AB=3,AE⊥BD,垂足为E,ED=3BE,点P、Q分别在BD、AD上,则AP+PQ最小值为 .
15. 如图,在矩形ABCD中,AB=3,AE⊥BD,垂足为E,ED=3BE,点P、Q分别在BD、AD上,则AP+PQ最小值为 . 16. 如图,在中, , 将绕点按逆时针方向旋转得到 . 若点恰好落在边上,且 , 则的度数为 .
16. 如图,在中, , 将绕点按逆时针方向旋转得到 . 若点恰好落在边上,且 , 则的度数为 .
三、解答题(共10题,共102分)
-
17.(1)、解方程:(2)、解不等式:18. 某工厂甲、乙两个部门各有员工400人,为了解这两个部门员工的生产技能情况,进行了抽样调查,过程如下,请补充完整.
【收集数据】
从甲、乙两个部门各随机抽取20名员工,进行了生产技能测试,测试成绩(百分制)如下:
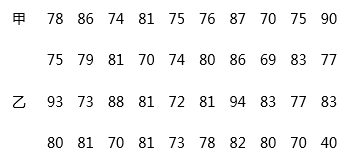
【整理、描述数据】
按如下分数段整理、描述这两组样本数据:
成绩
人数
部门
40≤x≤49
50≤x≤59
60≤x≤69
70≤x≤79
80≤x≤89
90≤x≤100
甲
0
0
1
11
7
1
乙
(说明:成绩80分及以上为生产技能优秀,70--79分为生产技能良好,60--69分为生产技能合格,60分以下为生产技能不合格)
【分析数据】
两组样本数据的平均数、中位数、众数如下表所示:
部门
平均数
中位数
众数
甲
78.3
77.5
75
乙
78
80.5
81
【得出结论】
.估计乙部门生产技能优秀的员工人数为;
.可以推断出部门员工的生产技能水平较高,理由为.(至少从两个不同的角度说明推断的合理性)
19. 即将在泰州举办的江苏省第20届运动会带动了我市的全民体育热,小明去某体育馆锻炼,该体育馆有A、B两个进馆通道和C、D、E三个出馆通道,从进馆通道进馆的可能性相同,从出馆通道出馆的可能性也相同.用列表或画树状图的方法,列出小明一次经过进馆通道与出馆通道的所有等可能的结果,并求他恰好经过通道A与通道D的概率.
20. 如图,O是矩形ABCD的对角线的交点,E,F,G,H分别是OA,OB,OC,OD上的点,且AE=BF=CG=DH.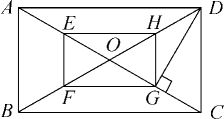 (1)、求证:四边形EFGH是矩形;(2)、若E,F,G,H分别是OA,OB,OC,OD的中点,且DG⊥AC,OF=2cm,求矩形ABCD的面积.21. 阅读下面材料:如图1,在平面直角坐标系xOy中,直线y1=ax+b与双曲线y2= 交于A(1,3)和B(﹣3,﹣1)两点,观察图象可知:①当x=﹣3或1时,y1=y2;②当﹣3<x<0或x>1时,y1>y2;即通过观察函数的图象,可以得到不等式ax+b> 的解集.
(1)、求证:四边形EFGH是矩形;(2)、若E,F,G,H分别是OA,OB,OC,OD的中点,且DG⊥AC,OF=2cm,求矩形ABCD的面积.21. 阅读下面材料:如图1,在平面直角坐标系xOy中,直线y1=ax+b与双曲线y2= 交于A(1,3)和B(﹣3,﹣1)两点,观察图象可知:①当x=﹣3或1时,y1=y2;②当﹣3<x<0或x>1时,y1>y2;即通过观察函数的图象,可以得到不等式ax+b> 的解集.
有这样一个问题:求不等式x3+4x2﹣x﹣4>0的解集.
艾斯柯同学类比以上知识的研究方法,用函数与方程的思想对不等式的解法进行了探究,请将他下面的②③④补充完整:
①当x=0时,原不等式不成立:当x>0时,原不等式可以转化为x2+4x﹣1> ;当x<0时,原不等式可以转化为x2+4x﹣1< .
②构造函数,画出图象
设y3=x2+4x﹣1,y4= 在同一坐标系中分别画出这两个函数的图象.
双曲线y4= 如图2所示,请在此坐标系中直接画出抛物线y3=x2+4x﹣1(可不列表);

③利用图象,确定交点横坐标
观察所画两个函数的图象,猜想并通过代入函数解析式验证可知:满足y3=y4的所有x的值为
④借助图象,写出解集
结合(1)的讨论结果,观察两个函数的图象可知:不等式x3+4x2﹣x﹣4>0的解集为
22. 小明同学在综合实践活动中对本地的一座古塔进行了测量.如图,他在山坡坡脚P处测得古塔顶端M的仰角为 ,沿山坡向上走25m到达D处,测得古塔顶端M的仰角为 .已知山坡坡度 ,即 ,请你帮助小明计算古塔的高度ME.(结果精确到0.1m,参考数据: ) 23. 公路上正在行驶的甲车发现前方处沿同一方向行驶的乙车后,开始减速,减速后甲车行驶的路程单位:、速度单位:与时间单位:的关系分别可以用二次函数和一次函数表示,其图象如图所示.
23. 公路上正在行驶的甲车发现前方处沿同一方向行驶的乙车后,开始减速,减速后甲车行驶的路程单位:、速度单位:与时间单位:的关系分别可以用二次函数和一次函数表示,其图象如图所示.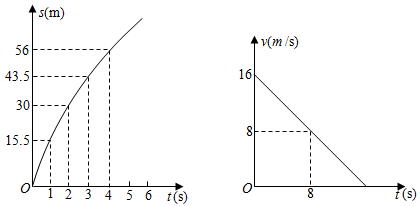 (1)、直接写出关于的函数关系式和关于的函数关系式不要求写出的取值范围(2)、当甲车减速至时,它行驶的路程是多少?(3)、若乙车以的速度匀速行驶,两车何时相距最近,最近距离是多少?24. 如图,对折矩形纸片ABCD,使AB与DC重合,得到折痕MN,将纸片展平;再一次折叠,使点D落到MN上的点F处,折痕AP交MN于E;延长PF交AB于G.
(1)、直接写出关于的函数关系式和关于的函数关系式不要求写出的取值范围(2)、当甲车减速至时,它行驶的路程是多少?(3)、若乙车以的速度匀速行驶,两车何时相距最近,最近距离是多少?24. 如图,对折矩形纸片ABCD,使AB与DC重合,得到折痕MN,将纸片展平;再一次折叠,使点D落到MN上的点F处,折痕AP交MN于E;延长PF交AB于G.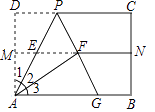 (1)、求证:△AFG≌△AFP;
(1)、求证:△AFG≌△AFP;
(2)、△APG为等边三角形.25. 如图,一次函数的图象经过 , 两点,与反比例函数的图象在第一象限内的交点为. (1)、求一次函数和反比例函数的表达式;(2)、点是线段上一点,若 , 求点的坐标;(3)、若点是轴上一点,是否存在以点、、为顶点的三角形是等腰三角形,若存在,求出点的坐标;若不存在,说明理由.26. 已知: ,过平面内一点 分别向 、 、 画垂线,垂足分别为 、 、 .
(1)、求一次函数和反比例函数的表达式;(2)、点是线段上一点,若 , 求点的坐标;(3)、若点是轴上一点,是否存在以点、、为顶点的三角形是等腰三角形,若存在,求出点的坐标;若不存在,说明理由.26. 已知: ,过平面内一点 分别向 、 、 画垂线,垂足分别为 、 、 .

 (1)、(问题引入)
(1)、(问题引入)
如图①,当点 在射线 上时,求证: .(2)、(类比探究)
如图②,当点 在 内部,点 在射线 上时,求证: .(3)、当点 在 内部,点 在射线 的反向延长线上时,在图③中画出示意图,并直接写出线段 、 、 之间的数量关系.(4)、(知识拓展)
如图④, 、 、 是 的三条弦,都经过圆内一点 ,且 .判断 与 的数量关系,并证明你的结论.