2024年江苏省常州市中考数学仿真模拟卷
试卷更新日期:2024-05-09 类型:中考模拟
一、单选题(每题2分,共16分)
-
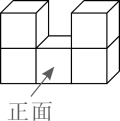
1. 下列运算中,计算正确的是( )A、 B、 C、 D、2. 若分式 的值为0,则x应满足的条件是( )A、 B、 C、 D、3. 如图,由5个完全相同的小正方体组合成一个立体图形,它的左视图为( )
 A、
A、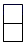 B、
B、 C、
C、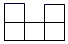 D、
D、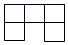 4. 的相反数是( )A、 B、 C、 D、5. 今年五月份香港举办“保普选反暴力”大联盟大型签名活动,9天共收集121万个签名,将121万用科学记数法表示为( )A、1.21×106 B、12.1×105 C、0.121×107 D、1.21×1056. 若点 与点 关于 轴对称,则A、2 B、0 C、-2 D、-47. 如图,已知点E、F分别是△ABC的边AB、AC上的点,且EF∥BC,点D是BC边上的点,AD与EF交于点H,则下列结论中,错误的是( )
4. 的相反数是( )A、 B、 C、 D、5. 今年五月份香港举办“保普选反暴力”大联盟大型签名活动,9天共收集121万个签名,将121万用科学记数法表示为( )A、1.21×106 B、12.1×105 C、0.121×107 D、1.21×1056. 若点 与点 关于 轴对称,则A、2 B、0 C、-2 D、-47. 如图,已知点E、F分别是△ABC的边AB、AC上的点,且EF∥BC,点D是BC边上的点,AD与EF交于点H,则下列结论中,错误的是( )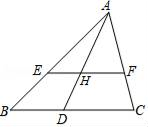 A、 B、 C、 D、8. 小明同学利用计算机软件绘制了某一函数的图象,如图所示.由学习函数的经验,可以推断这个函数可能是( )
A、 B、 C、 D、8. 小明同学利用计算机软件绘制了某一函数的图象,如图所示.由学习函数的经验,可以推断这个函数可能是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每题2分,共20分)
-
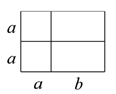
9. 当 时,二次根式 的值是.10. 分解因式: .11. 计算:| ﹣4|﹣( )﹣2= .12. 一货轮从甲港往乙港运送货物,甲港的装货速度是每小时30吨,一共装了8小时,到达乙港后开始卸货,乙港卸货的速度是每小时x吨,设卸货的时间是y小时,则y与x之间的函数关系式是 (不必写自变量取值范围).13. 下图中的四边形均为矩形,根据图形的面积关系,写出一个正确的等式: .
 14. 小华在如图所示的正方形网格纸板上玩飞镖游戏(每次飞镖均落在纸板上,且落在纸板的任何一个点的机会都相等),则飞镖落在阴影区域的概率是。
14. 小华在如图所示的正方形网格纸板上玩飞镖游戏(每次飞镖均落在纸板上,且落在纸板的任何一个点的机会都相等),则飞镖落在阴影区域的概率是。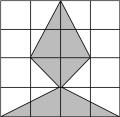
(第10题图)
15. 如图,在四边形ABCD中,AD=AB=BC,连接AC,且∠ACD=30°,tan∠BAC= ,CD=3,则AC= . 16. 在Rt△ABC中,∠C=90°,BC=3,AC=4,点P在以C为圆心,5为半径的圆上,连结PA,PB.若PB=4,则PA的长为 .
16. 在Rt△ABC中,∠C=90°,BC=3,AC=4,点P在以C为圆心,5为半径的圆上,连结PA,PB.若PB=4,则PA的长为 .
17. 如图,我国古代建造的闻名中外的赵州石拱桥,若桥拱圆弧的半径长为 , 拱高为 , 则桥跨度为(用含r、h的代数式表示)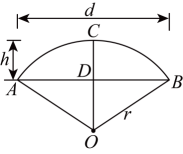 18. 在矩形 中, 点 是 边上的一个动点,连接 ,过点 作 与点 ,交射线 于点 ,连接 ,则 的最小值是
18. 在矩形 中, 点 是 边上的一个动点,连接 ,过点 作 与点 ,交射线 于点 ,连接 ,则 的最小值是
三、解答题(共10题,共84分)
-
19. 已知 , 求的值.20. 解不等式组: .21. 某校组织学生参加“防疫卫生知识竞赛”满分为分竞赛结束后,随机抽取甲、乙两班各名学生的成绩,并对数据成绩进行了整理、描述和分析下面给出了部分信息.
甲、乙两班各名学生数学成绩的频数分布统计表如下:
成绩
班级
甲
乙
说明:成绩分及以上为优秀,分为良好,分为合格,分以下为不合格
甲班成绩在这一组的是:
, , , , , , , , , , , ,
甲、乙两班成绩的平均分、中位数、众数如下:
班级
平均分
中位数
众数
甲
乙
根据以上信息,回答下列问题:
(1)、写出表中的值为 .(2)、在此次测试中,某学生的成绩是分,在他所属班级排在前名,由表中数据可知该学生是班的学生填“甲”或“乙” , 理由是 .(3)、假设学校名学生都参加此次竞赛,估计成绩优秀的学生人数.22. 如图是四张不透明的卡片.除正面分别有数字1、1、2、3 外.其他均相间.将这四张卡肯面朝上洗匀后放置在桌面上. (1)、小明从中随机抽取一张卡片,恰好得到数字1的概率是 .(2)、小明和小丽恕用这四张卡片做游戏,游戏规则为小明先随机抽取一张卡片,小丽再从余下的卡片中随机抽取一张.如朵两张卡片上的数字和为奇数,小明胜;和为偶数,小丽胜.你认为这个游戏公平吗?请用列表或画树状图的方法说明理由.23. 在菱形中,分别为上的点,且 , 连接并延长 , 与的延长线交于点 , 连接 .
(1)、小明从中随机抽取一张卡片,恰好得到数字1的概率是 .(2)、小明和小丽恕用这四张卡片做游戏,游戏规则为小明先随机抽取一张卡片,小丽再从余下的卡片中随机抽取一张.如朵两张卡片上的数字和为奇数,小明胜;和为偶数,小丽胜.你认为这个游戏公平吗?请用列表或画树状图的方法说明理由.23. 在菱形中,分别为上的点,且 , 连接并延长 , 与的延长线交于点 , 连接 . (1)、如图1,求证:四边形是平行四边形;(2)、如图2,连接 , 若 , 请直接写出长为线段长2倍的线段.24. 园林部门计划在公园建一个如图(甲)所示的长方形花圃 , 花圃的一面靠墙(墙足够长),另外三边用木栏围成, , 建成后所用木栏总长120米,在图(甲)总面积不变的情况下,在花圃内部设计了一个如图(乙)所示的正方形网红打卡点和两条宽度相等的小路,其中,小路的宽度是正方形网红打卡点边长的 , 其余部分种植花卉,花卉种植的面积为1728平方米.
(1)、如图1,求证:四边形是平行四边形;(2)、如图2,连接 , 若 , 请直接写出长为线段长2倍的线段.24. 园林部门计划在公园建一个如图(甲)所示的长方形花圃 , 花圃的一面靠墙(墙足够长),另外三边用木栏围成, , 建成后所用木栏总长120米,在图(甲)总面积不变的情况下,在花圃内部设计了一个如图(乙)所示的正方形网红打卡点和两条宽度相等的小路,其中,小路的宽度是正方形网红打卡点边长的 , 其余部分种植花卉,花卉种植的面积为1728平方米. (1)、求长方形花圃的长和宽;(2)、求出网红打卡点的面积.25. 如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数 的图象交于二四象限内的A、B 两点,与x轴交于C点,点B的坐标为(6,n),线段OA=5,E为x轴负半轴上一点,且sin∠AOE= .
(1)、求长方形花圃的长和宽;(2)、求出网红打卡点的面积.25. 如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数 的图象交于二四象限内的A、B 两点,与x轴交于C点,点B的坐标为(6,n),线段OA=5,E为x轴负半轴上一点,且sin∠AOE= . (1)、求该反比例函数和一次函数的解析式;
(1)、求该反比例函数和一次函数的解析式;
(2)、求△AOC的面积;
(3)、直接写出一次函数值大于反比例函数值时自变量x的取值范围.
26. 【温故知新】在证明“三角形的中位线平行于第三边,且等于第三边的一半”时,小明结合图1给出如下证明思路:作交的延长线于点 , 再证 , 再证四边形是平行四边形,即可证明定理。
图1 图2 图3 图4
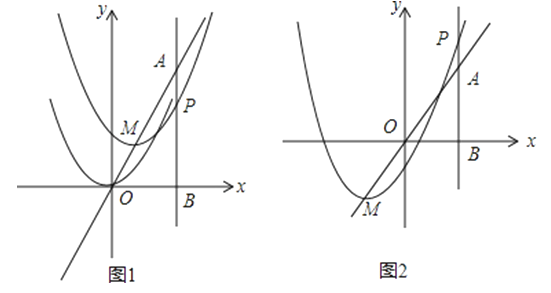
(1)、【新知体验】小明思考后发现:作平行线可以构成全等三角形或平行四边形,以达到解决问题的目的.如图2,在四边形中, , , 若 , , , 则的值为(2)、【灵活运用】如图3,在矩形和中,连接、交于点 , 连接。若 , 求的度数;(3)、【拓展延伸】如图4在第(2)题的条件下,连接 , 若 , 求的面积27.如图,在平面直角坐标系中,已知点A坐标为(2,4),直线x=2与x轴相交于点B,抛物线y=x2的顶点在直线AO上运动,与直线x=2交于点P,设平移后的抛物线顶点M的横坐标为m.
(1)如图1,若m=﹣1,求点P的坐标;
(2)在抛物线平移的过程中,当△PMA是等腰三角形时,求m的值;
(3)如图2,当线段BP最短时,相应的抛物线上是否存在点Q,使△QMA的面积与△PMA的面积相等?若存在,请求出点Q的坐标;若不存在,请说明理由.
 28.
28. (1)、【证明体验】
(1)、【证明体验】如图1,⊙O是等腰△ABC的外接圆,AB=AC , 在上取一点P , 连结AP , BP , CP . 求证:∠APB=∠PAC+∠PCA;
(2)、【思考探究】如图2,在(1)条件下,若点P为的中点,AB=6,PB=5,求PA的值;
(3)、【拓展延伸】如图3,⊙O的半径为5,弦BC=6,弦CP=5,延长AP交BC的延长线于点E , 且∠ABP=∠E , 求AP•PE的值.