2024年中考数学精选压轴之探究项目式学习(二)
试卷更新日期:2024-05-09 类型:三轮冲刺
一、实践探究题
-
1. 【项目化学习】
项目主题:从函数角度重新认识“阻力对物体运动的影响”.
项目内容:数学兴趣小组对一个静止的小球从斜坡滚下后,在水平木板上运动的速度、距离与时间的关系进行了深入探究,兴趣小组先设计方案,再进行测量,然后根据所测量的数据进行分析,并进一步应用。
实验过程:如图(a)所示,一个黑球从斜坡顶端由静止滚下沿水平木板直线运动,从黑球运动到点A处开始,用频闪照相机、测速仪测量并记录黑球在木板上的运动时间x(单位:s)、运动速度v(单位:cm/s)、滑行距离y(单位:cm)的数据.
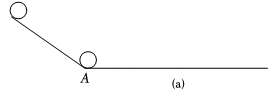
任务一:数据收集
记录的数据如下:
运动时间x/s
0
2
4
6
8
10
…
运动速度v/(cm/s)
10
9
8
7
6
5
…
滑行距离y/cm
0
19
36
51
64
75
…
根据表格中的数值分别在图(b)、图(c)中作出v与x的函数图象、y与x的函数图象:
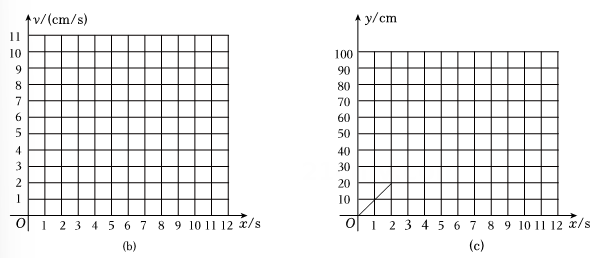 (1)、请在图(b)中画出v与x的函数图象:(2)、【任务二:观察分析】数学兴趣小组通过观察所作的函数图象,并结合已学习过的函数知识,发现图(b)中v与x的函数关系为一次函数关系,图(c)中y与x的函数关系为二次函数关系.请你结合表格数据,分别求出v与x的函数关系式和y与x的函数关系式:(不要求写出自变量的取值范围)(3)、【任务三:问题解决】当黑球在水平木板停下来时,求此时黑球的滑行距离:(4)、若黑球到达木板点A处的同时,在点A的前方处有一辆电动小车,以2cm/s的速度匀速向右直线运动,若黑球不能撞上小车,则n的取值范围应为 .2. 根据以下素材,探索完成任务.如何设计拱桥景观灯的悬挂方案?
(1)、请在图(b)中画出v与x的函数图象:(2)、【任务二:观察分析】数学兴趣小组通过观察所作的函数图象,并结合已学习过的函数知识,发现图(b)中v与x的函数关系为一次函数关系,图(c)中y与x的函数关系为二次函数关系.请你结合表格数据,分别求出v与x的函数关系式和y与x的函数关系式:(不要求写出自变量的取值范围)(3)、【任务三:问题解决】当黑球在水平木板停下来时,求此时黑球的滑行距离:(4)、若黑球到达木板点A处的同时,在点A的前方处有一辆电动小车,以2cm/s的速度匀速向右直线运动,若黑球不能撞上小车,则n的取值范围应为 .2. 根据以下素材,探索完成任务.如何设计拱桥景观灯的悬挂方案?素材1
图1中有一座拱桥,图2是某抛物线形桥拱的示意图,某时测得水面宽20m,拱顶离水面5m.据调查,该河段水位在此基础上再涨1.8m达到最高.

素材2
为迎佳节,拟在图1桥沿前面的桥拱上悬挂40cm长的灯笼,如图3.为了安全,灯笼底部距离水面不小于1m;为了实效,相邻两盏灯笼悬挂点的水平间距均为1.6m;为了美观,要求在符合条件处都挂上灯笼,且挂满后成轴对称分布.

问题解决(1)、任务1确定桥拱形状
在图2中建立合适的直角坐标系,求抛物线的函数表达式.
(2)、任务2探究悬挂范围
在你所建立的坐标系中,仅在安全的条件下,确定悬挂点的纵坐标的最小值和横坐标的取值范围.
(3)、任务3拟定设计方案
给出一种符合所有悬挂条件的灯笼数量,并根据你所建立的坐标系,求出最左边一盏灯笼悬挂点的横坐标.
3. 阅读素材,完成任务.测试机器人行走路径
素材一
图1是某校科技兴趣小组设计的一个可以帮助餐厅上菜的机器人,该机器人能根据指令要求进行旋转和行走.如图为机器人所走的路径.机器人从起点出发,连续执行如下指令:机器人先向前直行(表示第次行走的路程),再逆时针旋转 , 直到第一次回到起点后停止.记机器人共行走的路程为 , 所走路径形成的封闭图形的面积为S .

素材二
如图2,当每次直行路程均为1(即),时,机器人的运动路径为 , 机器人共走的路程 , 由图2图3易得所走路径形成的封闭图形的面积为 .

素材三
如图4,若 , 机器人执行六次指令后回到起点处停止.
解决问题
任务
固定变量
探索变量
探索内容
任务一
直行路程
旋转角度与路程
任务二
旋转角度
直行路程
若 , 求与的值.
任务三
旋转角度 , 路程
路径形成的封闭图形面积S .
若 , 请直接写出与之间的数量关系,并求出当S最大时的值.
4. 【综合与实践】根据以下素材,探索完成任务.素材1 图1中有一座拱桥,图2是其抛物线形桥拱的示意图,某时测得水面宽 , 拱顶离水面 . 据调查,该河段水位在此基础上再涨达到最高.

素材2 为迎佳节,拟在图1桥洞前面的桥拱上悬挂长的灯笼,如图3.为了安全,灯笼底部距离水面不小于;为了实效,相邻两盏灯笼悬挂点的水平间距均为;为了美观,要求在符合条件处都挂上灯笼,且挂满后成轴对称分布.
 (1)、任务1 确定桥拱形状:在图2中建立合适的直角坐标系,求抛物线的函数表达式.(2)、任务2 探究悬挂范围:在你所建立的坐标系中,仅在安全的条件下,确定悬挂点的纵坐标的最小值和横坐标的取值范围.(3)、任务3 拟定设计方案:请你设计一种符合所有悬挂条件的方案.5. 根据素材回答问题:
(1)、任务1 确定桥拱形状:在图2中建立合适的直角坐标系,求抛物线的函数表达式.(2)、任务2 探究悬挂范围:在你所建立的坐标系中,仅在安全的条件下,确定悬挂点的纵坐标的最小值和横坐标的取值范围.(3)、任务3 拟定设计方案:请你设计一种符合所有悬挂条件的方案.5. 根据素材回答问题:素材1
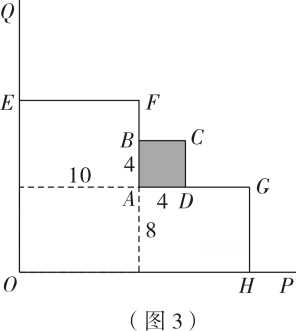
如图1,空地上有两条互相垂直的小路OP,OQ,中间有一正方形ABCD水池,已知水池的边长为4 米,AB//OQ,AD//OP,且AB与OQ的距离为10 米,AD与OP的距离为8 米.
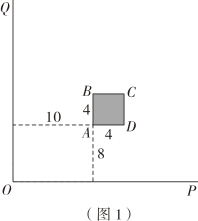
素材2
现利用两条小路,再购置30 米长的栅栏(图中的细实线)在空地上围出一个花圃,要求围起来的栅栏与小路相互平行(或垂直),靠小路和水池的都不需要栅栏,接口损耗忽略不计.
任务1
任务2
小明同学按如图2的设计,若EF=16米,求出花圃的面积(不包含水池的面积).
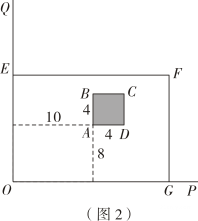
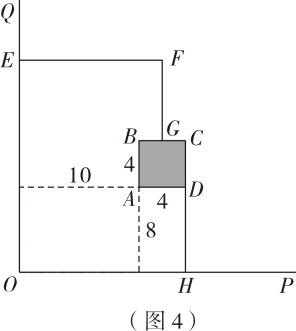
若按如图3、如图4设计方案,通过计算说明哪种方案的最大面积更大.
项目反 思
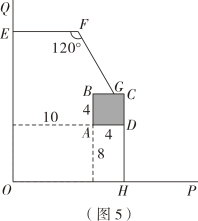
如果栅栏不一定与墙面垂直(或平行),你还能设计出比以上方案面积更大的花圃吗?某学习小组在探究的过程中,设计了方案如图5,你认为图5的最大面积与以上方案比较,哪个更大,请通过计算说明.
 6. 完成项目化学习:《蔬菜大棚的设计》.
6. 完成项目化学习:《蔬菜大棚的设计》.《蔬菜大棚的设计》
驱动问题
1、如何利用函数模型,刻画蔬菜大棚的棚面?
2、如何安装排气装置,保证蔬菜大棚的通风性?
3、如何设计大棚间距,保障蔬菜大棚的采光性?
项目背景
蔬菜大棚是一种具有出色的保温性能的框架覆膜结构,它出现使得人们可以吃到反季节蔬菜.如图,一般蔬菜大棚使用竹结构或者钢结构的骨架,这样就形成了一个温室空间.

数学建模
如图,某个温室大棚的横截面可以看作矩形ABCD和抛物线AED构成,其中AB=3m,取BC中点O,过点O作线段BC的垂直平分线OE交抛物线AED于点E,BC所在直线为x轴,OE为y轴建立如图所示平面直角坐标系.抛物线AED的顶点E(0,4)

问题解决
如图,为了保证该蔬菜大棚的通风性,该大棚要安装两个正方形孔的排气装置LFGT,若FL=NR=0.75m,求两个正方形装置的间距GM的长.

问题解决
为了保证两个蔬菜大棚间的采光不受影响,如图,在某一时刻,此时大棚截面的阴影为CK,求CK的长.
 7. 根据以下素材,探索完成任务.
7. 根据以下素材,探索完成任务.如何设计拱桥景观灯的悬挂方案?
素材1
图1中有一座拱桥,图2是其抛物线形桥拱的示意图,某时测得水面宽40m,拱顶离水面8m.据调查,该河段水位在此基础上再涨2.1m达到最高.

素材2
为迎佳节,拟在图1桥洞前面的桥拱上悬挂40cm长的灯笼,如图3.为了安全,灯笼底部距离水面不小于1m;为了实效,相邻两盏灯笼悬挂点的水平间距均为1.6m;为了美观,要求在符合条件处都挂上灯笼,且挂满后成轴对称分布.

问题解决
(1)、任务1:确定桥拱形状:在图2建立合适的直角坐标系,求抛物线的函数表达式.
(2)、任务2:探究悬挂范围:在你所建立的坐标系中,仅在安全的条件下,确定悬挂点的纵坐标的最小值和横坐标的取值范围.
(3)、任务3:拟定设计方案:给出一种符合所有悬挂条件的灯笼数量,并根据你所建立的坐标系,求出最左边一盏灯笼悬挂点的横坐标.
8. 根据以下素材,探索完成任务.如何设计警戒线之间的宽度?
素材1

图1为某公园的抛物线型拱桥,图2是其横截面示意图,测得水面宽度AB=24米,拱顶离水面的距离为CD=4米.
素材2
拟在公园里投放游船供游客乘坐,载重最少时,游船的横
截面如图3所示,漏出水面的船身为矩形,船顶为等腰三
角形.测得相关数据如下:EF=EK=1.7米,FK=3米,
GH=IJ=1.26米,FG=JK=0.4米.

素材3
为确保安全,拟在石拱桥下面的P , Q两处设置航行警戒线,要求如下:
①游船底部HI在P , Q之间通行;
②当载重最少通过时,游船顶部E与拱桥的竖直距离至少为0.5米.
问题解决
(1)、任务1:确定拱桥形状在图2中建立合适的直角坐标系,并求这条抛物线的函数表达式.
(2)、任务2:设计警戒线之间的宽度求PQ的最大值.
9. 根据以下素材,探索完成任务.如何设计喷泉安全通道?
在抛物线形的喷泉水柱下设置一条安全的通道,可以让儿童在任意时间穿过安全通道时不被水柱喷到(穿梭过程中人的高度变化忽略不计).
素材1
图1为音乐喷泉,喷头的高度在垂直地面的方向上随着音乐变化而上下移动.不同高度的喷头喷出来的水呈抛物线型或抛物线的一部分,但形状相同,最高高度也相同,水落地点都在喷水管的右侧.

素材2
图2是当喷水头在地面上时(喷水头最低),其抛物线形水柱的示意图,水落地点离喷水口的距离为 , 水柱最高点离地面 .
图3是某一时刻时,水柱形状的示意图.为喷水管,为水的落地点,记长度为喷泉跨度.


素材3
安全通道在线段上,若无论喷头高度如何变化,水柱都不会进入上方的矩形区域,则称这个矩形区域为安全区域.

问题解决
任务1
确定喷泉形状.
在图2中,以为原点,所在直线为轴,建立平面直角坐
标系,求出抛物线的函数表达式.
任务2
确定喷泉跨度的最小值.
若喷水管最高可伸长到 , 求出喷泉跨度的最小值.
任务3
设计通道位置及儿童的身高上限.
现在需要一条宽为的安全通道 , 为了确保进入安全通道
上的任何人都能在安全区域内,则能够进入该安全通道的人
的最大身高为多少?(精确到)
10. 综合与实践优化洒水车为公路两侧绿化带浇水效率
信息1
如图1,洒水车沿着平行于公路路牙方向行驶,喷水口H离地竖直高度OH为1.5m.

信息2
如图2,可以把洒水车喷出水的内、外边缘抽象为平面直角坐标系中两条抛物线的部分图象;把绿化带横截面抽象为矩形DEFG,其水平宽度DE=3m,竖直高度EF=0.5m.内边缘抛物线y2是由外边缘抛物线y1向左平移得到,外边抛物线y1最高点A离喷水口的水平距离为2m,高出喷水口0.5m.
问题解决
任务1
确定浇灌方式
(1)求外边缘抛物线y1的函数解析式,并求喷出水的最大射程OC;
(2)直接写出内边缘抛物线y与x轴的正半轴交点B的坐标;
任务2
提倡有效浇灌
(3)要使洒水车行驶时喷出的水能浇灌到整个绿化带,求OD的取值范围.
11. 根据以下材料,探索完成任务:智能浇灌系统使用方案
材料

如图1是一款智能浇灌系统,水管OP垂直于地面并可以随意调节高度(OP最大高度不超过2.4m),浇灌花木时,喷头P处会向四周喷射水流形成固定形状的抛物线,水流落地点M与点O的距离即为最大浇灌距离,各方向水流落地点形成一个以点O为圆心,OM为半径的圆形浇灌区域.
当喷头P位于地面与点O重合时,某一方向的水流上边缘形成了如图2的抛物线,经测量, , 水流最高时距离地面0.1m.
如图3,农科院将该智能浇灌系统应用于一个长8m,宽6m的矩形试验田中,水管放置在矩形中心O处.
问题解决
任务1
确定水流形状
在图2中建立合适的平面直角坐标系,求抛物线的函数表达式.
任务2
探究浇灌最大区域
当调节水管OP的高度时,浇灌的圆形区域面积会发生变化,请你求出最大浇灌圆形区域面积.(结果保留)
任务3
解决具体问题
若要保证浇灌区域能完全覆盖矩形试验田,则水管OP至少需要调节到什么高度?
12. 根据以下素材,探索完成任务如何调整足球的发球方向
素材1
如图是某足球场的一部分,球门宽DE=CF=7m,高CD=EF=2.5m,小梅站在A处向门柱CD一侧发球,点A正对门柱CD(即AC⊥CF),AC=24m,足球运动的路线是抛物线的一部分.

素材2
如图,当足球运动到最高点时,高度为4.5m,即 , 此时水平距离 , 以点为原点,直线BA为轴,建立平面直角坐标系.

素材3
距离球门正前方6m处放置一块矩形拦网HGMN,拦网面垂直于地面,且GH∥CF,拦网高HN=4m.

问题解决
任务1
结合素材1,2,求足球运动的高度与水平距离之间的函数关系式.
任务2
结合素材1,2,小梅不改变发球的方向,射门路线的形状和最大高度保持不变此时足球能否进入球门?若不能进入,他应该带球向正后方至少移动多少米射门才能让足球进入球门
任务3
结合以上素材,小梅站在A处,只改变发球方向,射门路线的形状和最大高度保持不变,请探求此时足球能否越过拦网,在点E处进入球门
上述任务1、任务2、任务3中球落在门柱边线视同足球进入球门
13. 根据以下素材,探索完成任务.如何选择合适的跳台高度?

素材1 跳台滑雪是运动员借助速度和弹跳力,沿着跳台下滑,并从起跳点腾空,在空中沿抛物线飞行至着陆坡.图1是某小型跳台滑雪训练场的实物图,图2是其横截面示意图,以地面的水平线为x轴,过跳台终点A作水平线的垂线为y轴,建立平面直角坐标系,图中的抛物线C1近似表示滑雪场地上的一座小山坡,其最左端位于点O的正上方米处,最右端在水平线上,且最高点在距O点水平距离8米处.
素材2 小雪从点O正上方米处的A点滑出,滑出后沿一段抛物线C2:y=a(x−7)2+8运动.该滑雪场有若干个跳台高度不同,小山坡完全相同的训练场地,在不同场地滑行时,小雪滑行的抛物线形状不变.
(1)、任务1 确定滑行路径 求a的值;(2)、任务2 确定山坡形状 当小雪滑行到离A处的水平距离为11米时,恰好落在小山坡上,求抛物线C1的函数表达式;(3)、任务3 选择跳台高度 若小雪选择的跳台高度增加了米,请判断在该训练场地滑行时是否会落在小山坡上.14. 根据以下素材,探索完成任务如何设计拱桥上救生圈的悬挂方案?
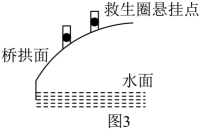
素材1
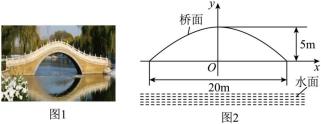
图1是一座抛物线形拱桥,以抛物线两个水平最低点连线为x轴,抛物线离地面的最高点的铅垂线为y轴建立平面直角坐标系,如图2所示.
某时测得水面宽 , 拱顶离水面最大距离为10m,抛物线拱形最高点与x轴的距离为5m.据调查,该河段水位在此基础上再涨1m达到最高.
素材2
为方便救助溺水者,拟在图1的桥拱上方栏杆处悬挂救生圈,如图3,救生圈悬挂点为了方便悬挂,救生圈悬挂点距离抛物线拱面上方1m,且相邻两救生圈悬挂点的水平间距为4m.为美观,放置后救生圈关于y轴成轴对称分布.(悬挂救生圈的柱子大小忽略不计)
任务1
确定桥拱形状
根据图2,求抛物线的函数表达式.
任务2
拟定设计方案
求符合悬挂条件的救生圈个数,并求出最右侧一个救生圈悬挂点的坐标.
任务3
探究救生绳长度
当水位达到最高时,上游个落水者顺流而下到达抛物线拱形桥面的瞬间,若要确保救助者把拱桥上任何一处悬挂点的救生圈抛出都能抛到落水者身边,求救生绳至少需要多长.(救生圈大小忽略不计,结果保留整数)
问题解决
(1)、任务1 确定桥拱形状根据图2,求抛物线的函数表达式.
(2)、任务2 拟定设计方案求符合悬挂条件的救生圈个数,并求出最右侧一个救生圈悬挂点的坐标.
(3)、任务3 探究救生绳长度当水位达到最高时,上游个落水者顺流而下到达抛物线拱形桥面的瞬间,若要确保救助者把拱桥上任何一处悬挂点的救生圈抛出都能抛到落水者身边,求救生绳至少需要多长.(救生圈大小忽略不计,结果保留整数)
15. 根据以下素材,探究完成任务素材1 图1是一个瓷碗,图2是其截面图,碗体DEC呈抛物线状(碗体厚度不计),碗高GF=7cm,碗底宽AB=3cm,当瓷碗中装满面汤时,液面宽CD= 12cm,
此时面汤最大深度EG= 6cm,
素材2 如图3,把瓷碗绕点B缓缓倾斜倒出部分面汤,当点A离MN距离为1.8cm时停止.

问题解决 任务1 确定碗体形状 在图2中建立合适的直角坐标系,求抛物线的函数表达式。
任务2 拟定设计方案1 根据图2位置,把碗中面汤喝掉一部分,当碗中液面高度(离桌面MN距离)为5cm时,求此时碗中液面宽度。
任务3 拟定设计方案2 如图3,当碗停止倾斜时,求此时碗中液面宽度CH。
16. 根据以下素材,探索完成任务.绿化带灌溉车的操作方案
素材1
辆绿化带灌溉车正在作业,水从喷水口喷出,水流的上下两边缘可以抽象为两条抛物线的一部分:喷水口离开地面高1.6米,上边缘抛物线最高点离喷水口的水平距离为3米,高出|喷水口0.9米,下边缘水流形状与上边缘相同,且喷水口是最高点。

素材2
路边的绿化带宽4米
素材3
绿化带正中间种植了行道树,为了防治病虫害、增加行道树的成活率,园林工人给树木“打针”。针一般打在离地面1.5米到2米的高度(包含端点)。

问题解决
(1)、任务1:确定上边缘水流形状建立如图所示直角坐标系,求上边缘抛物线的函数表达式.
(2)、任务2:探究灌溉范围灌溉车行驶过程中喷出的水能浇浓到整个绿化带吗?请说明理由.
(3)、任务3:拟定设计方案灌溉时,发现水流的上下两边缘冲击力最强,喷到针筒容易造成针筒脱落。那么请问在满足最大灌溉面积的前提下对行道树“打针”是否有影响,并说明理由;若你认为有影响,请给出具体的“打针”范围。
17. 根据以下素材,探索完成任务.如何设计喷泉喷头的升降方案?
素材1
如图,有一个可垂直升降的喷泉,喷出的水柱呈抛物线.记水柱上某一点到喷头的水平距离为x米,到湖面的垂直高度为y米.当喷头位于起始位置时,测量得x与y的四组数据如下:
x(米)
0
2
3
4
y(米)
1
2
1.75
1

素材2
公园想设立新的游玩项目,通过升降喷头,使游船能从水柱下方通过,如图,为避免游船被喷泉淋到,要求游船从水柱下方中间通过时,顶棚上任意一点到水柱的竖直距离均不小于0.4米.已知游船顶棚宽度为2.8米,顶棚到湖面的高度为2米.

问题解决
任务1
确定喷泉形状
结合素材1,求y关于x的表达式.
任务2
探究喷头升降方案
为使游船按素材2要求顺利通过,求喷头距离湖面高度的最小值.
18. 根据以下素材,探索完成任务.如何设计跳长绳方案
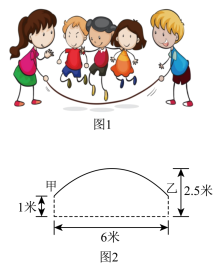
素材1
图1是集体跳长绳比赛,比赛时,各队跳绳10人,摇绳2人,共计12人.图2是绳甩到最高处时的示意图,可以近似的看作一条抛物线,正在甩绳的甲、乙两位队员拿绳的手间距6米,到地面的距离均为1米,绳子最高点距离地面2.5米.
素材2
某队跳绳成员有6名男生和4名女生,男生身高1.70米至1.80米,女生身高1.66米至1.68米.跳长绳比赛时,可以采用一路纵队或两路纵队并排的方式安排队员位置,但为了保证安全,人与人之间距离至少0.5米.
问题解决
任务1
确定长绳形状
在图2中建立合适的直角坐标系,并求出抛物线的函数表达式.
任务2
探究站队方式
当该队以一路纵队的方式跳绳时,绳子能否顺利的甩过所有队员的头顶?
任务3
拟定位置方案
为了更顺利的完成跳绳,现按中间高两边低的方式居中安排站位.请在你所建立的坐标系中,求出左边第一位跳绳队员横坐标的最大取值范围.
19. 许多数学问题源于生活.雨伞是生活中的常用物品,我们用数学的眼光观察撑开后的雨伞(如图①)、可以发现数学研究的对象——抛物线.在如图②所示的直角坐标系中,伞柄在y轴上,坐标原点O为伞骨 , 的交点.点C为抛物线的顶点,点A,B在抛物线上, , 关于y轴对称.分米,点A到x轴的距离是分米,A,B两点之间的距离是4分米.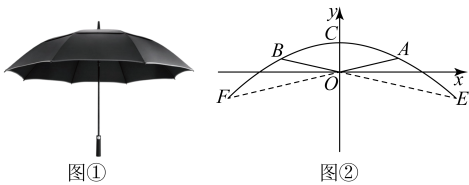 (1)、求抛物线的表达式;(2)、分别延长 , 交抛物线于点F,E,求E,F两点之间的距离;(3)、以抛物线与坐标轴的三个交点为顶点的三角形面积为 , 将抛物线向右平移个单位,得到一条新抛物线,以新抛物线与坐标轴的三个交点为顶点的三角形面积为 . 若 , 求m的值.20. 乒乓球被誉为中国国球.2023年的世界乒乓球标赛中,中国队包揽了五个项目的冠军,成绩的取得与平时的刻苦训练和精准的技术分析是分不开的.如图,是乒乓球台的截面示意图,一位运动员从球台边缘正上方以击球高度为的高度,将乒乓球向正前方击打到对面球台,乒乓球的运行路线近似是抛物线的一部分.
(1)、求抛物线的表达式;(2)、分别延长 , 交抛物线于点F,E,求E,F两点之间的距离;(3)、以抛物线与坐标轴的三个交点为顶点的三角形面积为 , 将抛物线向右平移个单位,得到一条新抛物线,以新抛物线与坐标轴的三个交点为顶点的三角形面积为 . 若 , 求m的值.20. 乒乓球被誉为中国国球.2023年的世界乒乓球标赛中,中国队包揽了五个项目的冠军,成绩的取得与平时的刻苦训练和精准的技术分析是分不开的.如图,是乒乓球台的截面示意图,一位运动员从球台边缘正上方以击球高度为的高度,将乒乓球向正前方击打到对面球台,乒乓球的运行路线近似是抛物线的一部分.
乒乓球到球台的竖直高度记为(单位:),乒乓球运行的水平距离记为(单位:).测得如下数据:
水平距离x/
竖直高度y/
(1)、在平面直角坐标系中,描出表格中各组数值所对应的点 , 并画出表示乒乓球运行轨迹形状的大致图象; (2)、①当乒乓球到达最高点时,与球台之间的距离是 , 当乒乓球落在对面球台上时,到起始点的水平距离是 ;
(2)、①当乒乓球到达最高点时,与球台之间的距离是 , 当乒乓球落在对面球台上时,到起始点的水平距离是 ;②求满足条件的抛物线解析式;
(3)、技术分析:如果只上下调整击球高度 , 乒乓球的运行轨迹形状不变,那么为了确保乒乓球既能过网,又能落在对面球台上,需要计算出的取值范围,以利于有针对性的训练.如图②.乒乓球台长为274 , 球网高为15.25 . 现在已经计算出乒乓球恰好过网的击球离度的值约为1.27 . 请你计算出乒乓球恰好落在对面球台边缘点B处时,击球高度的值(乒乓球大小忽略不计).