2024年中考数学精选压轴题之旋转问题
试卷更新日期:2024-05-09 类型:三轮冲刺
一、选择题(每题3分,共36分)
-
1. 如图,在△ABC中,∠ACB=90°,AC=2,AB=4,将△ABC绕点C按逆时针方向旋转一定的角度得到△DEC,使得A点恰好落在DE上,则线段BD的长为( )
 A、2 B、5 C、2 D、32. 如图,将边长为的正方形绕点逆时针旋转得到正方形 , 与交于点 , 那么图中点的坐标为( )
A、2 B、5 C、2 D、32. 如图,将边长为的正方形绕点逆时针旋转得到正方形 , 与交于点 , 那么图中点的坐标为( ) A、 B、 C、 D、3. 如图所示,矩形ABOC的顶点O(0,0),A(-2 , 2),对角线交点为P,若矩形绕点O逆时针旋转,每次旋转90°,则第74次旋转后点P的落点坐标为( )
A、 B、 C、 D、3. 如图所示,矩形ABOC的顶点O(0,0),A(-2 , 2),对角线交点为P,若矩形绕点O逆时针旋转,每次旋转90°,则第74次旋转后点P的落点坐标为( ) A、(1,) B、(2,0) C、(1,-) D、( , -1)4. 如图,点是等边内一点,将线段绕点沿顺时针方向旋转得到线段 , 连接 , , 若 , , , 则下列结论正确的有( )个.
A、(1,) B、(2,0) C、(1,-) D、( , -1)4. 如图,点是等边内一点,将线段绕点沿顺时针方向旋转得到线段 , 连接 , , 若 , , , 则下列结论正确的有( )个.
①为等边三角形;
②;
③;
④ .
A、1 B、2 C、3 D、45. 如图,P是正方形内一点, , 则正方形的面积是( )
 A、 B、13 C、 D、6. 如图,和都是等腰直角三角形, , 点是边上的动点(不与点B、C重合),与交于点 , 连结下列结论:;;若 , 则;在内存在唯一一点 , 使得的值最小,若点在的延长线上,且的长为2,则其中含所有正确结论的选项是( )
A、 B、13 C、 D、6. 如图,和都是等腰直角三角形, , 点是边上的动点(不与点B、C重合),与交于点 , 连结下列结论:;;若 , 则;在内存在唯一一点 , 使得的值最小,若点在的延长线上,且的长为2,则其中含所有正确结论的选项是( )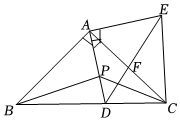 A、 B、 C、 D、7. 如图,在中, , , 将绕点顺时针旋转得到 , 点A、B的对应点分别是 , , 点是边的中点,连接 , , .则下列结论错误的是( )
A、 B、 C、 D、7. 如图,在中, , , 将绕点顺时针旋转得到 , 点A、B的对应点分别是 , , 点是边的中点,连接 , , .则下列结论错误的是( )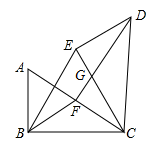 A、 B、 , C、 D、8. 如图,四边形为正方形,将绕点逆时针旋转至 , 点 , , 在同一直线上,与交于点 , 延长与的延长线交于点 , , .以下结论:
A、 B、 , C、 D、8. 如图,四边形为正方形,将绕点逆时针旋转至 , 点 , , 在同一直线上,与交于点 , 延长与的延长线交于点 , , .以下结论:①;②;③;④.其中正确结论的个数为( )
 A、1个 B、2个 C、3个 D、4个9. 如图,正方形的边长为2,对角线、相交于点 , 把放在正方形上,使直角顶点与点重合,让绕着点旋转,、分别交、于点、 , 给出下列结论;①;②;③.其中正确的结论是( )
A、1个 B、2个 C、3个 D、4个9. 如图,正方形的边长为2,对角线、相交于点 , 把放在正方形上,使直角顶点与点重合,让绕着点旋转,、分别交、于点、 , 给出下列结论;①;②;③.其中正确的结论是( ) A、①②③ B、①② C、②③ D、①③10. 如图,已知Rt△ABC, , 将△ABC绕点A沿逆时针方向旋转后得到△ADE,直线BD、CE相交于点F,连接AF,则下列结论中:①;②△ABD∽△ACE;③;④F为BD的中点,其中正确的有( )
A、①②③ B、①② C、②③ D、①③10. 如图,已知Rt△ABC, , 将△ABC绕点A沿逆时针方向旋转后得到△ADE,直线BD、CE相交于点F,连接AF,则下列结论中:①;②△ABD∽△ACE;③;④F为BD的中点,其中正确的有( )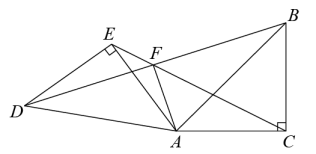 A、①②③ B、①②④ C、①②③④ D、②③④11. 如图,等边三角形ABC的边长为2,点O是△ABC的中心,∠FOG=120°,将∠FOG绕点O旋转,分别交线段AB、BC于D、E两点,连接DE , 给出下列四个结论:①OD=OE;②S四边形ODBE= S△ABC;③S△ODE=S△BDE;④△BDE周长的最小值为3.上述结论中正确的个数是( )
A、①②③ B、①②④ C、①②③④ D、②③④11. 如图,等边三角形ABC的边长为2,点O是△ABC的中心,∠FOG=120°,将∠FOG绕点O旋转,分别交线段AB、BC于D、E两点,连接DE , 给出下列四个结论:①OD=OE;②S四边形ODBE= S△ABC;③S△ODE=S△BDE;④△BDE周长的最小值为3.上述结论中正确的个数是( ) A、1 B、2 C、3 D、412. 四边形 中, ,则 的值为( )
A、1 B、2 C、3 D、412. 四边形 中, ,则 的值为( ) A、15 B、 C、 D、20
A、15 B、 C、 D、20二、填空题(每题3分,共18分)
-
13. 在△ABC中,∠ACB=90°,∠B=60°,AB=8,点D是直线BC上动点,连接AD,在直线AD的右侧作等边△ADE,连接CE,当线段CE的长度最小时,线段CD的长度为 .
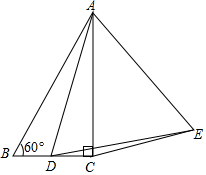 14. 如图正方形的边长为3,E是上一点且 , F是线段上的动点.连接 , 将线段绕点C逆时针旋转 90°得到 , 连接 , 则的最小值是 .
14. 如图正方形的边长为3,E是上一点且 , F是线段上的动点.连接 , 将线段绕点C逆时针旋转 90°得到 , 连接 , 则的最小值是 .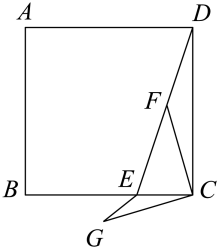 15. 如图,已知:中, , , 为线段上一点,将线段绕点逆时针旋转得到线段 , 为中点,直线交射线于点 , 下列说法,若连接 , 则;;;若 , 则其中正确的序号有 .
15. 如图,已知:中, , , 为线段上一点,将线段绕点逆时针旋转得到线段 , 为中点,直线交射线于点 , 下列说法,若连接 , 则;;;若 , 则其中正确的序号有 .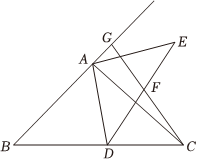 16. 如图,将绕点顺时针旋转,使点落在边上的点处,点落在点处,与相交于点 , 若 , , , 则的长为 .
16. 如图,将绕点顺时针旋转,使点落在边上的点处,点落在点处,与相交于点 , 若 , , , 则的长为 . 17. 如图,为直角三角形, , , , D是边上的中点,将绕着点A逆时针旋转,使点C落在线段上的点E处,点B的对应点为F , 边与边交于点G , 则的长是.
17. 如图,为直角三角形, , , , D是边上的中点,将绕着点A逆时针旋转,使点C落在线段上的点E处,点B的对应点为F , 边与边交于点G , 则的长是. 18. 如图,长方形ABCD中,AB=6,BC=8,E为BC上一点,且BE=2,F为AB边上的一个动点,连接EF , 将EF绕着点E顺时针旋转30°到EG的位置,连接FG和CG , 则CG的最小值为 .
18. 如图,长方形ABCD中,AB=6,BC=8,E为BC上一点,且BE=2,F为AB边上的一个动点,连接EF , 将EF绕着点E顺时针旋转30°到EG的位置,连接FG和CG , 则CG的最小值为 .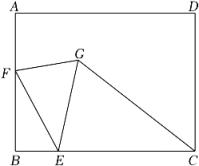
三、解答题(共6题,共46分)
-
19. 在等边△ABC中,BC=4,点D是AB的中点,点E,F分别是CD,AC边上一点(不与点A,C重合).
 (1)、如图1,当点E为CD中点,点F为AC中点时,求EF的长度.(2)、如图2,将线段CE绕着点C顺时针旋转60°得到线段CP,连结AP,当B,E,P三点在同一条直线上时,求AP的长度.(3)、如图3,将线段FE绕着点F顺时针旋转60°得到线段FQ,延长QE交线段BC于点M,探索CF,CM,CE三条线段之间的关系.20. 如图,为的中线,以为直角边在其右侧作直角 , , 与交于点F , .
(1)、如图1,当点E为CD中点,点F为AC中点时,求EF的长度.(2)、如图2,将线段CE绕着点C顺时针旋转60°得到线段CP,连结AP,当B,E,P三点在同一条直线上时,求AP的长度.(3)、如图3,将线段FE绕着点F顺时针旋转60°得到线段FQ,延长QE交线段BC于点M,探索CF,CM,CE三条线段之间的关系.20. 如图,为的中线,以为直角边在其右侧作直角 , , 与交于点F , . (1)、如图1,若 , 求的长;(2)、如图2,若将绕点C逆时针旋转得到 , 连接、 , 探究、的数量关系,并说明理由;(3)、如图3,若 , , , 直线上有一点M , 连接 , 将沿着翻折到所在的平面内得到 , 取的中点P , 连接 , 当最小时,请直接写出的面积.21. 在中, , , 为平面内的一点.
(1)、如图1,若 , 求的长;(2)、如图2,若将绕点C逆时针旋转得到 , 连接、 , 探究、的数量关系,并说明理由;(3)、如图3,若 , , , 直线上有一点M , 连接 , 将沿着翻折到所在的平面内得到 , 取的中点P , 连接 , 当最小时,请直接写出的面积.21. 在中, , , 为平面内的一点.图1
 图2
图2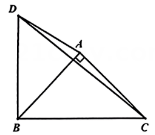 图3
图3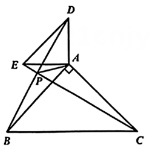 (1)、如图1,当点在边上时, , 且 , 求的长;(2)、如图2,当点在的外部,且满足 , 求证:;(3)、如图3, , 当、分别为、的中点时,把绕点顺时针旋转,设旋转角为 , 直线与的交点为 , 连接 , 直接写出旋转中面积的最大值.22. 已知点C为和的公共顶点,将绕点C顺时针旋转 , 连接 , , 请完成如下问题:
(1)、如图1,当点在边上时, , 且 , 求的长;(2)、如图2,当点在的外部,且满足 , 求证:;(3)、如图3, , 当、分别为、的中点时,把绕点顺时针旋转,设旋转角为 , 直线与的交点为 , 连接 , 直接写出旋转中面积的最大值.22. 已知点C为和的公共顶点,将绕点C顺时针旋转 , 连接 , , 请完成如下问题: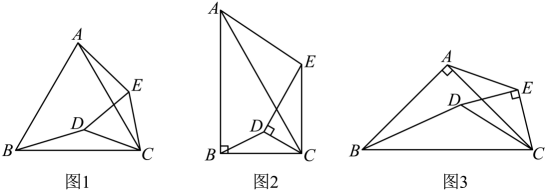 (1)、如图1,若和均为等边三角形,①线段与线段的数量关系是;②直线与直线相交所夹锐角的度数是;
(1)、如图1,若和均为等边三角形,①线段与线段的数量关系是;②直线与直线相交所夹锐角的度数是;类比探究:
(2)、如图2,若 , , 其他条件不变,则(1)中的结论是否都成立?请说明理由;(3)、拓展应用:如图3,若 , , , , 当点B,D,E三点共线时,请直接写出的长.23. 如图,在等边中,于点 , 为线段上一动点(不与 , 重合),连接 , , 将绕点顺时针旋转得到线段 , 连接 .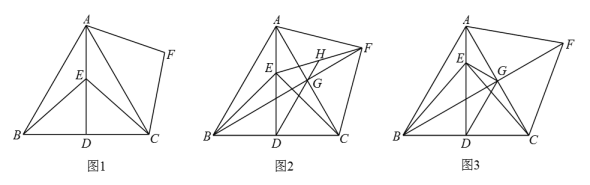 (1)、如图1,求证:;(2)、如图2,连接交于点 , 连接 , , 与所在直线交于点 , 求证:;(3)、如图3,连接交于点 , 连接 , , 将沿所在直线翻折至所在平面内,得到 , 将沿所在直线翻折至所在平面内,得到 , 连接 , . 若 , 直接写出的最小值.24. “转化”是解决数学问题的重要思想方法,通过构造图形全等或者相似建立数量关系是处理问题的重要手段.
(1)、如图1,求证:;(2)、如图2,连接交于点 , 连接 , , 与所在直线交于点 , 求证:;(3)、如图3,连接交于点 , 连接 , , 将沿所在直线翻折至所在平面内,得到 , 将沿所在直线翻折至所在平面内,得到 , 连接 , . 若 , 直接写出的最小值.24. “转化”是解决数学问题的重要思想方法,通过构造图形全等或者相似建立数量关系是处理问题的重要手段.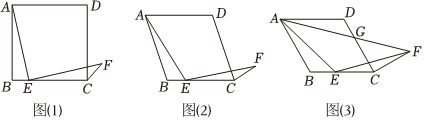 (1)、【问题情景】:如图 , 正方形中,点是线段上一点不与点、重合 , 连接将绕点顺时针旋转得到 , 连接 , 求的度数.
(1)、【问题情景】:如图 , 正方形中,点是线段上一点不与点、重合 , 连接将绕点顺时针旋转得到 , 连接 , 求的度数.以下是两名同学通过不同的方法构造全等三角形来解决问题的思路,
①小聪:过点作的延长线的垂线;
②小明:在上截取 , 使得;
请你选择其中一名同学的解题思路,写出完整的解答过程.
(2)、【类比探究】:如图点是菱形边上一点不与点、重合 , , 将绕点顺时针旋转得到 , 使得 , 则的度数为用含的代数式表示 .(3)、【学以致用】:如图 , 在的条件下,连结 , 与相交于点 , 当时,若 , 求的值.