2024年江苏省南通市中考数学仿真模拟卷
试卷更新日期:2024-05-09 类型:中考模拟
一、单选题(每题3分,共30分)
-
1. 计算(﹣2)2×(﹣4)的正确结果是( )A、16 B、-8 C、-16 D、82. 党的二十大报告指出,我国建成世界上规模最大的教育体系、社会保障体系、医疗卫生体系,教育普及水平实现历史性跨越,基本养老保险覆盖十亿四千万人,基本医疗保险参保率稳定在百分之九十五.将数据1040000000用科学记数法表示为( )A、 B、 C、 D、3. 下面四个几何体中,主视图、左视图、俯视图是全等图形的几何图形是( )A、圆柱 B、正方体 C、三棱柱 D、圆锥4. 估计的值( )A、在1到2之间 B、在2到3之间 C、在3到4之间 D、在4到5之间5. 如图, , .若 , 则的大小为( )
 A、 B、 C、 D、6. 抛物线y=ax2+bx﹣3过点(2,4),则代数式8a+4b+1的值为( )A、-2 B、2 C、15 D、-157. 如图,在一个20米高的楼顶上有一信号塔DC,某同学为了测量信号塔的高度,在地面的A处测得信号塔下端D的仰角为30°,然后他正对塔的方向前进了8米到达地面的B处,又测得信号塔顶端C的仰角为45°,CD⊥AB于点E,E、B、A在一条直线上.信号塔CD的高度为( )
A、 B、 C、 D、6. 抛物线y=ax2+bx﹣3过点(2,4),则代数式8a+4b+1的值为( )A、-2 B、2 C、15 D、-157. 如图,在一个20米高的楼顶上有一信号塔DC,某同学为了测量信号塔的高度,在地面的A处测得信号塔下端D的仰角为30°,然后他正对塔的方向前进了8米到达地面的B处,又测得信号塔顶端C的仰角为45°,CD⊥AB于点E,E、B、A在一条直线上.信号塔CD的高度为( ) A、20 B、20﹣8 C、20﹣28 D、20﹣208. 在以“矩形的折叠”为主题的数学活动课上,某位同学进行了如下操作:
A、20 B、20﹣8 C、20﹣28 D、20﹣208. 在以“矩形的折叠”为主题的数学活动课上,某位同学进行了如下操作:第一步:将矩形纸片的一端,利用图①的方法折出一个正方形ABEF,然后把纸片展平;
第二步:将图①中的矩形纸片折叠,使点恰好落在点处,得到折痕 , 如图②.
根据以上的操作,若 , 则线段的长是( )
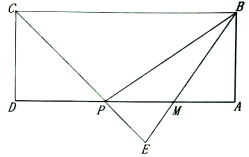
 A、3 B、 C、2 D、19. 如图,在矩形中,P是边上的一个动点,连接 , , 过点B作射线,交线段的延长线于点E,交边于点M,且使得 , 如果 , , , , 其中 . 则下列结论中,正确的个数为( )
A、3 B、 C、2 D、19. 如图,在矩形中,P是边上的一个动点,连接 , , 过点B作射线,交线段的延长线于点E,交边于点M,且使得 , 如果 , , , , 其中 . 则下列结论中,正确的个数为( )⑴y与x的关系式为;(2)当时,;(3)当时, .
 A、0个 B、1个 C、2个 D、3个10. 已知二次函数 ( 为常数),当自变量 的值满足 时,与其对应的函数值 的最大值为-3,则 的值为( )A、3或4 B、0或4 C、0或7 D、7或3
A、0个 B、1个 C、2个 D、3个10. 已知二次函数 ( 为常数),当自变量 的值满足 时,与其对应的函数值 的最大值为-3,则 的值为( )A、3或4 B、0或4 C、0或7 D、7或3二、填空题(每题3分,共24分)
-
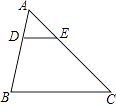
11. 计算:的结果为 .12. 因式分解:2a2-2=.13. 如图,△ABC中,D、E分别在AB、AC上,DE∥BC,AD:AB=1:3,则△ADE与△ABC的面积之比为 .
 14. 已知蓄电池的电压恒定,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示,如果以此蓄电池为电源的用电器,流过的电流是2A,那么此用电器的电阻是Ω.
14. 已知蓄电池的电压恒定,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示,如果以此蓄电池为电源的用电器,流过的电流是2A,那么此用电器的电阻是Ω.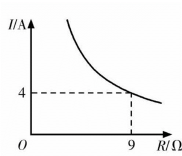 15. 如图,在⊙O中,BC是直径,弦BA , CD的延长线相交于点P , 若∠P=50°,则∠AOD= .
15. 如图,在⊙O中,BC是直径,弦BA , CD的延长线相交于点P , 若∠P=50°,则∠AOD= . 16. 一列数a1 , a2 , a3 , …满足条件:a1= ,an= (n≥2,且n为整数),则a1+a2+a3+…+a2021= .17. 函数的函数值随自变量的增大而减小,下列描述中:;函数图象与轴的交点为;函数图象经过第一象限;点在该函数图象上,正确的描述有 填写番号18. 如图,在 中, , , 为 边的中点,点E、F分别是线段AC、AD上的动点,且 ,则 的最小值是.
16. 一列数a1 , a2 , a3 , …满足条件:a1= ,an= (n≥2,且n为整数),则a1+a2+a3+…+a2021= .17. 函数的函数值随自变量的增大而减小,下列描述中:;函数图象与轴的交点为;函数图象经过第一象限;点在该函数图象上,正确的描述有 填写番号18. 如图,在 中, , , 为 边的中点,点E、F分别是线段AC、AD上的动点,且 ,则 的最小值是.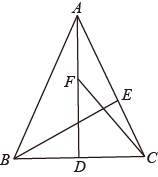
三、解答题(共8题,共96分)
-
19.(1)、化简:(2)、解不等式组:20. 为了提高某城区居民的生活质量,政府将改造城区配套设施,并随机向某居民小区发放调查问卷(1人只能投1票),共有休闲设施,儿童设施,娱乐设施,健身设施4种选项,一共调查了a人,其调查结果如下:
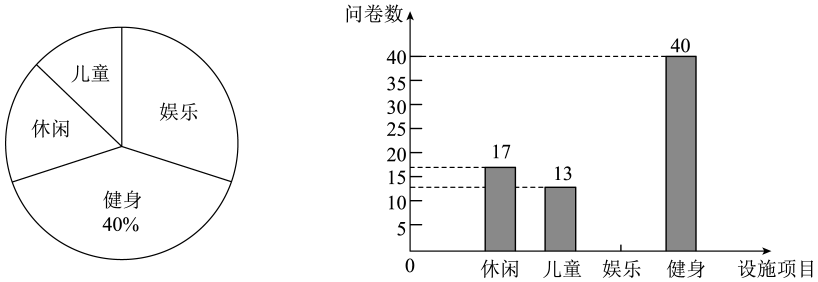
如图,为根据调查结果绘制的扇形统计图和条形统计图,请根据统计图回答下面的问题:
①调查总人数 人;
②请补充条形统计图;
③若该城区共有10万居民,则其中愿意改造“娱乐设施”的约有多少人?
④改造完成后,该政府部门向甲、乙两小区下发满意度调查问卷,其结果(分数)如下:
项目
小区
休闲
儿童
娱乐
健身
甲
7
7
9
8
乙
8
8
7
9
若以1:1:1:1进行考核, 小区满意度(分数)更高;
若以1:1:2:1进行考核, 小区满意度(分数)更高.
21. 如图,矩形中, , 点M是的中点,连接 . 将沿着折叠后得 , 延长交于E , 连接 . (1)、求证:平分;(2)、求证:△EMC∽△MAB.22. 第31届世界大学生夏季运动会于2023年7月28日-8月8日在成都举行.彬彬和明明申请足球A、篮球B、排球C、乒乓球D . 四项赛事中某一项的志愿者,他们被随机分配到这四项赛事中的任意一项的可能性相同.(1)、“彬彬被分配到乒乓球D . 赛事做志愿者”是事件(填“必然”、“不可能”或“随机”).(2)、请用画树状图法或列表法,求彬彬和明明被分配到同一项赛事做志愿者的概率.23. 如图所示,以▱ABCD的顶点A为圆心,AB为半径作圆,分别交AD,BC于点E,F,延长BA交⊙A于点G.
(1)、求证:平分;(2)、求证:△EMC∽△MAB.22. 第31届世界大学生夏季运动会于2023年7月28日-8月8日在成都举行.彬彬和明明申请足球A、篮球B、排球C、乒乓球D . 四项赛事中某一项的志愿者,他们被随机分配到这四项赛事中的任意一项的可能性相同.(1)、“彬彬被分配到乒乓球D . 赛事做志愿者”是事件(填“必然”、“不可能”或“随机”).(2)、请用画树状图法或列表法,求彬彬和明明被分配到同一项赛事做志愿者的概率.23. 如图所示,以▱ABCD的顶点A为圆心,AB为半径作圆,分别交AD,BC于点E,F,延长BA交⊙A于点G. (1)、求证:;(2)、若∠C=120°,BG=4,求阴影部分弓形的面积.24. 为弘扬中华民族传统文化,某校举办了“古诗文大赛”,并为获奖同学购买签字笔和笔记本作为奖品.1支签字笔和2个笔记本共8.5元,2支签字笔和3个笔记本共13.5元.
(1)、求证:;(2)、若∠C=120°,BG=4,求阴影部分弓形的面积.24. 为弘扬中华民族传统文化,某校举办了“古诗文大赛”,并为获奖同学购买签字笔和笔记本作为奖品.1支签字笔和2个笔记本共8.5元,2支签字笔和3个笔记本共13.5元.(1)求签字笔和笔记本的单价分别是多少元?
(2)为了激发学生的学习热情,学校决定给每名获奖同学再购买一本文学类图书,如果给每名获奖同学都买一本图书,需要花费720元;书店出台如下促销方案:购买图书总数超过50本可以享受8折优惠.学校如果多买12本,则可以享受优惠且所花钱数与原来相同.问学校获奖的同学有多少人?
25. 如图1,在矩形ABCD中, , M,N,P,Q分别从A,B,C,D出发,沿AD,BC,CB,DA方向在矩形的边上同时运动,运动速度分别是1cm/s,2cm/s,tcm/s, , 当其中一个点到达所在运动边的另一个端点时,四个点同时停止运动.设运动时间为t秒. (1)、当t为何值时,点M,Q重合;(2)、当以P,Q,M,N为顶点的四边形是平行四边形时,求t的值或范围;(3)、如题图2,连接BD,交MN于点E,交PQ于点F,当t为何值时,.26. 我们把与轴有两个不同交点的函数称为“五好函数”,交点称为“五好点”,两交点间的距离称为“五好距”.(1)、判断下列函数是“五好函数”吗?如果是,请在括号里打“”,如果不是则打“”;
(1)、当t为何值时,点M,Q重合;(2)、当以P,Q,M,N为顶点的四边形是平行四边形时,求t的值或范围;(3)、如题图2,连接BD,交MN于点E,交PQ于点F,当t为何值时,.26. 我们把与轴有两个不同交点的函数称为“五好函数”,交点称为“五好点”,两交点间的距离称为“五好距”.(1)、判断下列函数是“五好函数”吗?如果是,请在括号里打“”,如果不是则打“”;
▲ ;;(2)、求出“五好函数”的“五好距”;(3)、已知“五好函数”:左侧的“五好点”位于和之间含 , 两点 , 求的取值范围;
不论取何值,不等式恒成立,在的条件下,函数为常数的最小值为 , 求的值.