2024年中考数学精选压轴题之相似三角形
试卷更新日期:2024-05-09 类型:三轮冲刺
一、选择题
-
1. 如图,在平面直角坐标系中,点 , 将线段AB平移得到线段DC.若 , 则点的坐标为( )
 A、 B、 C、 D、2. 如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE . 将△ADE沿AE对折至△AFE , 延长EF交边BC于点G , 连接AG、CF . 下列结论:①△ABG≌△AFG;②BG=GC;③AG//CF;④S△FGC=3.其中正确结论的个数是( )
A、 B、 C、 D、2. 如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE . 将△ADE沿AE对折至△AFE , 延长EF交边BC于点G , 连接AG、CF . 下列结论:①△ABG≌△AFG;②BG=GC;③AG//CF;④S△FGC=3.其中正确结论的个数是( ) A、1 B、2 C、3 D、43. 如图,在正方形ABCD中,是等边三角形,BP、CP的延长线分别交AD于点E、F , 连接BD、DP , BD与CF相交于点H , 给出下列结论:①;②∽;③∽;④ , 其中正确的是( )
A、1 B、2 C、3 D、43. 如图,在正方形ABCD中,是等边三角形,BP、CP的延长线分别交AD于点E、F , 连接BD、DP , BD与CF相交于点H , 给出下列结论:①;②∽;③∽;④ , 其中正确的是( ) A、①②③④ B、②③ C、①②④ D、①③④4. 如图,在平面直角坐标系中,矩形的边 . , 将矩形沿直线折叠到如图所示的位置,线段恰好经过点 , 点落在轴的点位置,点的坐标是
A、①②③④ B、②③ C、①②④ D、①③④4. 如图,在平面直角坐标系中,矩形的边 . , 将矩形沿直线折叠到如图所示的位置,线段恰好经过点 , 点落在轴的点位置,点的坐标是 A、 B、 C、 , D、 ,5. 如图,已知AB=AC , ∠B<30°,BC上一点D满足∠BAD=120°,= , 则的值为( )
A、 B、 C、 , D、 ,5. 如图,已知AB=AC , ∠B<30°,BC上一点D满足∠BAD=120°,= , 则的值为( ) A、 B、 C、 D、6. 如图,AB是⊙O的直径,弦CD⊥AB于点E , 在BC上取点F , 使得CF=CE , 连结AF交CD于点G , 连结AD . 若CG=GF , 则的值等于( )
A、 B、 C、 D、6. 如图,AB是⊙O的直径,弦CD⊥AB于点E , 在BC上取点F , 使得CF=CE , 连结AF交CD于点G , 连结AD . 若CG=GF , 则的值等于( ) A、 B、 C、 D、7. 如图,已知是的中线,E是线段上一点,且 , 的延长线交于点,则的值为( )
A、 B、 C、 D、7. 如图,已知是的中线,E是线段上一点,且 , 的延长线交于点,则的值为( ) A、 B、 C、 D、8. 如图,已知平行四边形 , 点E是延长线上一点,与分别相交于点 . 则下列关系式成立的是( )
A、 B、 C、 D、8. 如图,已知平行四边形 , 点E是延长线上一点,与分别相交于点 . 则下列关系式成立的是( ) A、 B、 C、 D、9. 如图,在正方形中,点分别是边上的两点,且分别交于 . 对于下列结论:
A、 B、 C、 D、9. 如图,在正方形中,点分别是边上的两点,且分别交于 . 对于下列结论:①;②;③;④当时,面积的最小值为 . 其中正确的是( )
 A、①② B、②③ C、①②③ D、①②③④10. 如图,在正方形ABCD中,AD=4,E为CD中点,F为BC上的一点,且∠EAF=45°,∠ABG=∠DAE,连接EF,延长BG交AE于点M,交AD于点N,则以下结论;
A、①② B、②③ C、①②③ D、①②③④10. 如图,在正方形ABCD中,AD=4,E为CD中点,F为BC上的一点,且∠EAF=45°,∠ABG=∠DAE,连接EF,延长BG交AE于点M,交AD于点N,则以下结论;①DE+BF=EF②BN⊥AE③BF=④S△BGF=中正确的是( )
 A、1个 B、2个 C、3个 D、4个11. 如图,在矩形中, , 点分别在边上,且与关于直线对称.点在边上,分别与交于两点.若 , , 则( )
A、1个 B、2个 C、3个 D、4个11. 如图,在矩形中, , 点分别在边上,且与关于直线对称.点在边上,分别与交于两点.若 , , 则( )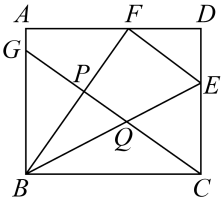 A、 B、 C、 D、12. 如图,将正方形纸片ABCD沿PQ折叠,使点C的对称点E落在边AB上,点D的对称点为点F,EF为交AD于点G,连接CG交PQ于点H,连接CE.下列四个结论中:①△PBE∽△QFG;②S△CEG=S△CBE+S四边形CDQH;③EC平分∠BEG;④EG2﹣CH2=GQ•GD,正确的是( )
A、 B、 C、 D、12. 如图,将正方形纸片ABCD沿PQ折叠,使点C的对称点E落在边AB上,点D的对称点为点F,EF为交AD于点G,连接CG交PQ于点H,连接CE.下列四个结论中:①△PBE∽△QFG;②S△CEG=S△CBE+S四边形CDQH;③EC平分∠BEG;④EG2﹣CH2=GQ•GD,正确的是( ) A、①③ B、①③④ C、①④ D、①②③④
A、①③ B、①③④ C、①④ D、①②③④二、填空题
-
13. 在锐角中,AD , BE分别为的中线和角平分线, , 且 , 则.
 14. 如图,在矩形ABCD中,E是AB的中点,作交BC于点F , 对角线AC分别交DE , DF于点G , H , 当DH⊥AC时,则的值为 .
14. 如图,在矩形ABCD中,E是AB的中点,作交BC于点F , 对角线AC分别交DE , DF于点G , H , 当DH⊥AC时,则的值为 .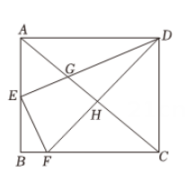 15. 如图,正方形中,M、N分别是、边上的点,将四边形沿直线翻折,使得点A、B分别落在点、处,且点恰好为线段的中点,交于点G , 作于点P , 交于点Q . 若 , 则 .
15. 如图,正方形中,M、N分别是、边上的点,将四边形沿直线翻折,使得点A、B分别落在点、处,且点恰好为线段的中点,交于点G , 作于点P , 交于点Q . 若 , 则 . 16. 如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,CD⊥AB,垂足为D,E为BC的中点,AE与CD交于点F,则DF的长为 .
16. 如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,CD⊥AB,垂足为D,E为BC的中点,AE与CD交于点F,则DF的长为 .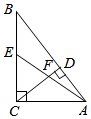 17. 如图,平分等边的面积,折叠得到 , 分别与 , 相交于 , 两点.若 , , 则的长是 .
17. 如图,平分等边的面积,折叠得到 , 分别与 , 相交于 , 两点.若 , , 则的长是 . 18. 如图,中, , , 点D在上, . 点E在上,且 , 则的值为 .
18. 如图,中, , , 点D在上, . 点E在上,且 , 则的值为 .
三、解答题
-
19. 已知和都是等腰三角形,且 , , 若点D在边上运动时,总保持 , 连接与交于点F .
 (1)、①如图1,当点D为边中点时,则的值为 ▲ ;
(1)、①如图1,当点D为边中点时,则的值为 ▲ ;②如图2,当点D不为边中点时,求证:;
(2)、如图3,当点D在边上运动中恰好使得时,若 , , 求的长.20. 如图,将矩形ABCD绕点C顺时针旋转,使点A,F,E三点共线,得到对应矩形EFCG,连接AF,AC,DG,DE.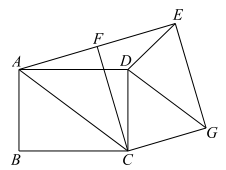 (1)、求证:AF=CG;(2)、判断DG与AC的位置关系,并说明理由;(3)、若AB=3,BC=4,求tan∠AED的值.21. 在中, , D是边上一动点,E是外一点,连接 .
(1)、求证:AF=CG;(2)、判断DG与AC的位置关系,并说明理由;(3)、若AB=3,BC=4,求tan∠AED的值.21. 在中, , D是边上一动点,E是外一点,连接 . (1)、如图1, , , 若 , 求的度数;(2)、如图2, , , 过点D作交于点F , 若 , 求证:;(3)、如图3, , 延长交的延长线于点F , 交于点G , 点D是直线上一动点,将沿翻折得 , 连接 , 取的中点M , 连接 , 若 , 当线段取得最大值时,请直接写出的值.22. 如图1,在平面直角坐标系中,点的坐标为 , 以点为圆心,5为半径的圆与坐标轴分别交于点、、、 .
(1)、如图1, , , 若 , 求的度数;(2)、如图2, , , 过点D作交于点F , 若 , 求证:;(3)、如图3, , 延长交的延长线于点F , 交于点G , 点D是直线上一动点,将沿翻折得 , 连接 , 取的中点M , 连接 , 若 , 当线段取得最大值时,请直接写出的值.22. 如图1,在平面直角坐标系中,点的坐标为 , 以点为圆心,5为半径的圆与坐标轴分别交于点、、、 . (1)、与相似吗?为什么?(2)、如图2,弦交轴于点 , 且 , 求;(3)、如图3,过点作的切线,交轴于点 . 点是上的动点,问比值是否变化?若不变,请求出比值;若变化,请说明理由.23. 在中, , , 为边上一动点,且为正整数 , 在直线上方作 , 使得∽ .
(1)、与相似吗?为什么?(2)、如图2,弦交轴于点 , 且 , 求;(3)、如图3,过点作的切线,交轴于点 . 点是上的动点,问比值是否变化?若不变,请求出比值;若变化,请说明理由.23. 在中, , , 为边上一动点,且为正整数 , 在直线上方作 , 使得∽ .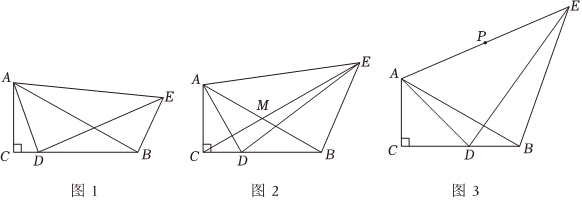 (1)、如图 , 在点运动过程中,与始终保持相似关系,请说明理由;(2)、如图 , 若 , 为中点,当点在射线上时,求的长;(3)、如图 , 设的中点为 , 求点从点运动到点的过程中,点运动的路径长用含的代数式表示 .24. 如图①,在矩形ABCD中,AB=4,AD=6,点E在边BC上,且BE=2,动点P从点E出发,沿折线EB﹣BA﹣AD以每秒1个单位长度的速度运动.作∠PEQ=90°,EQ交边AD或边DC于点Q,连接PQ.当点Q与点C重合时,点P停止运动.设点P的运动时间为t秒.(t>0)
(1)、如图 , 在点运动过程中,与始终保持相似关系,请说明理由;(2)、如图 , 若 , 为中点,当点在射线上时,求的长;(3)、如图 , 设的中点为 , 求点从点运动到点的过程中,点运动的路径长用含的代数式表示 .24. 如图①,在矩形ABCD中,AB=4,AD=6,点E在边BC上,且BE=2,动点P从点E出发,沿折线EB﹣BA﹣AD以每秒1个单位长度的速度运动.作∠PEQ=90°,EQ交边AD或边DC于点Q,连接PQ.当点Q与点C重合时,点P停止运动.设点P的运动时间为t秒.(t>0) (1)、当点P和点B重合时,线段PQ的长为 ;(2)、当点Q和点D重合时,求的值;(3)、当点P在边AD上运动时,如图②,求证:为定值,并求这个值;(4)、作点E关于直线PQ的对称点F,连接PF、QF,当四边形EPFQ和矩形ABCD的重叠部分为轴对称四边形时,直接写出t的取值范围.
(1)、当点P和点B重合时,线段PQ的长为 ;(2)、当点Q和点D重合时,求的值;(3)、当点P在边AD上运动时,如图②,求证:为定值,并求这个值;(4)、作点E关于直线PQ的对称点F,连接PF、QF,当四边形EPFQ和矩形ABCD的重叠部分为轴对称四边形时,直接写出t的取值范围.