2024年江苏省淮安市中考数学仿真模拟卷
试卷更新日期:2024-05-09 类型:中考模拟
一、选择题(每题3分,共24分)
-
1. 下列各数中的无理数是( )A、 B、 C、 D、2. 下列图形中,既是轴对称图形是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 原子钟是以原子的规则振动为基础的各种守时装置的统称,其中氢脉泽钟的精度达到了1700000年误差不超过1秒.数据1700000用科学记数法表示( )A、 B、 C、 D、4. 下列式子中,计算正确的是( )A、a3+a3=a6 B、(﹣a2)3=﹣a6 C、a2•a3=a6 D、(a+b)2=a2+b25. 实数a , b , c在数轴上对应的点如图所示,下列判断正确的是( )
3. 原子钟是以原子的规则振动为基础的各种守时装置的统称,其中氢脉泽钟的精度达到了1700000年误差不超过1秒.数据1700000用科学记数法表示( )A、 B、 C、 D、4. 下列式子中,计算正确的是( )A、a3+a3=a6 B、(﹣a2)3=﹣a6 C、a2•a3=a6 D、(a+b)2=a2+b25. 实数a , b , c在数轴上对应的点如图所示,下列判断正确的是( ) A、 B、 C、 D、6. 如图,将一副三角板在平行四边形ABCD中作如下摆放,设 ,那么 ( )
A、 B、 C、 D、6. 如图,将一副三角板在平行四边形ABCD中作如下摆放,设 ,那么 ( )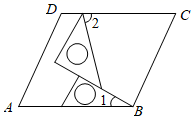 A、 B、 C、 D、7. 已知某几何体的三视图(单位:cm)如图所示,则该几何体的侧面积和侧面展开图圆心角的度数为( )
A、 B、 C、 D、7. 已知某几何体的三视图(单位:cm)如图所示,则该几何体的侧面积和侧面展开图圆心角的度数为( ) A、12πcm2和215° B、15πcm2和216° C、24πcm2和217° D、30πcm2和218°8. 如图,在平面直角坐标系中,直线y=-3x+3交x轴于点A,交y轴于点B,以AB为边在第一象限作正方形ABCD,其中顶点D恰好落在双曲线y=k/x上,现将正方形ABCD沿y轴向下平移a个单位长度,可以使得顶点C落在双曲线上,则a的值为( )
A、12πcm2和215° B、15πcm2和216° C、24πcm2和217° D、30πcm2和218°8. 如图,在平面直角坐标系中,直线y=-3x+3交x轴于点A,交y轴于点B,以AB为边在第一象限作正方形ABCD,其中顶点D恰好落在双曲线y=k/x上,现将正方形ABCD沿y轴向下平移a个单位长度,可以使得顶点C落在双曲线上,则a的值为( )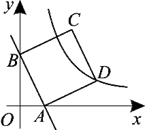 A、 B、 C、2 D、
A、 B、 C、2 D、二、填空题(每题3分,共24分)
-
9. 使根式 有意义的x的取值范围是 .10. 分式方程的解是 .11. 若一条长为32cm的细线能围成一边长等于8cm的等腰三角形,则该等腰三角形的腰长为cm.12. 已知 , 代数式 .13. 甲、乙、丙、丁四人进行射击测试,每人10次射击成绩的平均数均是9.2环,方差分别为 , 则这四人中成绩最稳定的是.14. 如图,是直径,点B、C、D在半圆上,若 , 则 .
 15. 如图,四边形中, , , , 满足 , 则面积的最小值为 .
15. 如图,四边形中, , , , 满足 , 则面积的最小值为 . 16. 矩形的边 . 点为平面内一点, , 若 , 则 .
16. 矩形的边 . 点为平面内一点, , 若 , 则 .三、解答题(共11题,共102分)
-
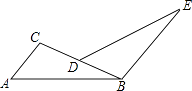
17. 已知关于x , y的方程组的解满足不等式 , 求m的负整数解.18. 先化简,再求值: , 其中x满足方程 .19. 已知:如图,点D在△ABC的BC边上,AC∥BE,BC=BE,∠ABC=∠E,求证:AB=DE.
 20. 有4张正面分别写有数字1,2,3,4的不透明卡片,它们除数字外完全相同,将它们背面朝上洗匀.(1)、随机抽取一张,求抽到数字为奇数的概率.(2)、随机抽取两张,记下两张卡片的数字,用列表或画树状图求抽取的两张卡片上数字之和为奇数的概率.21. “惜餐为荣,殄物为耻”,为了解落实“光盘行动”的情况,某校调研了七、八年级部分 班级某一天的餐后垃圾质量.从七、八年级各随机抽取10个班餐后垃圾质量的数据(单位:),进行整理和分析(餐后垃圾质量用x 表示,共分为四个等级:A.;B.;C.;D.),下面给出了部分信息.
20. 有4张正面分别写有数字1,2,3,4的不透明卡片,它们除数字外完全相同,将它们背面朝上洗匀.(1)、随机抽取一张,求抽到数字为奇数的概率.(2)、随机抽取两张,记下两张卡片的数字,用列表或画树状图求抽取的两张卡片上数字之和为奇数的概率.21. “惜餐为荣,殄物为耻”,为了解落实“光盘行动”的情况,某校调研了七、八年级部分 班级某一天的餐后垃圾质量.从七、八年级各随机抽取10个班餐后垃圾质量的数据(单位:),进行整理和分析(餐后垃圾质量用x 表示,共分为四个等级:A.;B.;C.;D.),下面给出了部分信息.七年级10个班餐后垃圾质量: .
八年级10个班餐后垃圾质量中B 等级包含的所有数据为: .
七八年级抽取的班级餐后垃圾质量统计表
年级
平均数
中位数
众数
方差
A等级所占百分比
七年级
a
八年级
b
八年级抽取的班级餐后垃圾质量扇形统计图
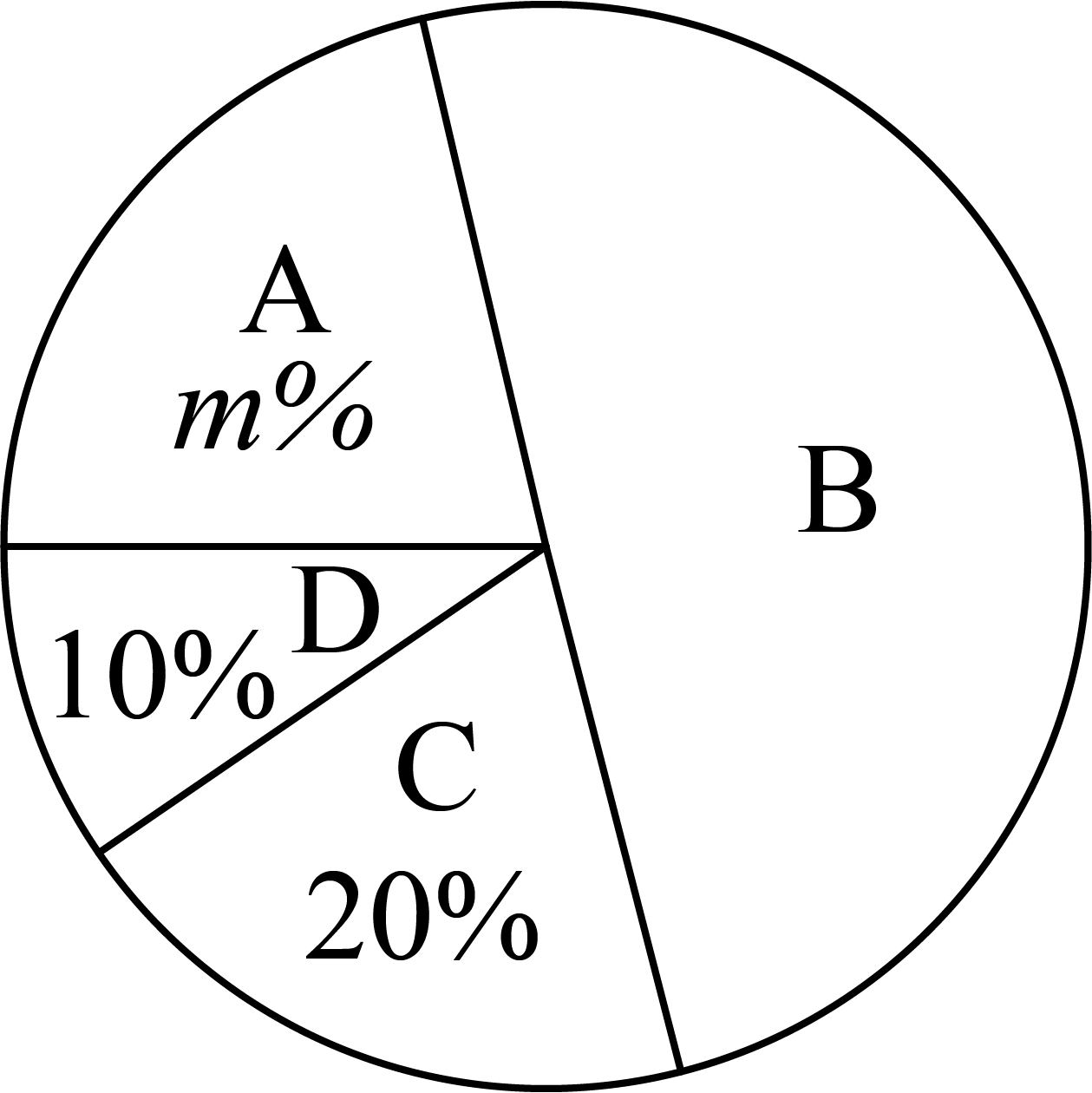 (1)、直接写出上述表中a,b,m 的值;(2)、该校八年级共有30个班,估计八年级这一天餐后垃圾质量符合A 等级的班级数;(3)、根据以上信息,你认为该校七、八年级的“光盘行动”,哪个年级落实得更好?请说明理由(写出一条理由即可).22. 如图,某小区矩形绿地的长宽分别为30m,20m.现计划对其进行扩充,将绿地的长、宽增加相同的长度后,得到一个新的矩形绿地.若扩充后的矩形绿地面积为 , 求新的矩形绿地的长与宽.
(1)、直接写出上述表中a,b,m 的值;(2)、该校八年级共有30个班,估计八年级这一天餐后垃圾质量符合A 等级的班级数;(3)、根据以上信息,你认为该校七、八年级的“光盘行动”,哪个年级落实得更好?请说明理由(写出一条理由即可).22. 如图,某小区矩形绿地的长宽分别为30m,20m.现计划对其进行扩充,将绿地的长、宽增加相同的长度后,得到一个新的矩形绿地.若扩充后的矩形绿地面积为 , 求新的矩形绿地的长与宽. 23. 如图,小华和同伴秋游时,发现在某地小山坡的点E处有一棵小树,他们想利用皮尺、倾角器和平面镜测量小树到山脚下的距离(即DE的长度),小华站在点B处,让同伴移动平面镜至点C处,此时小华在平面镜内可以看到点E.且测得BC=3米,CD=28米.∠CDE=127°.已知小华的眼睛到地面的距离AB=1.5米,请根据以上数据,求DE的长度.(参考数据: , )
23. 如图,小华和同伴秋游时,发现在某地小山坡的点E处有一棵小树,他们想利用皮尺、倾角器和平面镜测量小树到山脚下的距离(即DE的长度),小华站在点B处,让同伴移动平面镜至点C处,此时小华在平面镜内可以看到点E.且测得BC=3米,CD=28米.∠CDE=127°.已知小华的眼睛到地面的距离AB=1.5米,请根据以上数据,求DE的长度.(参考数据: , ) 24. 学校与图书馆在同一条笔直道路上,甲从学校去图书馆,乙从图书馆回学校,甲、乙两人都匀速步行且同时出发,乙先到达目的地.两人之间的距离y(米)与时间t(分钟)之间的函数关系如图所示.
24. 学校与图书馆在同一条笔直道路上,甲从学校去图书馆,乙从图书馆回学校,甲、乙两人都匀速步行且同时出发,乙先到达目的地.两人之间的距离y(米)与时间t(分钟)之间的函数关系如图所示.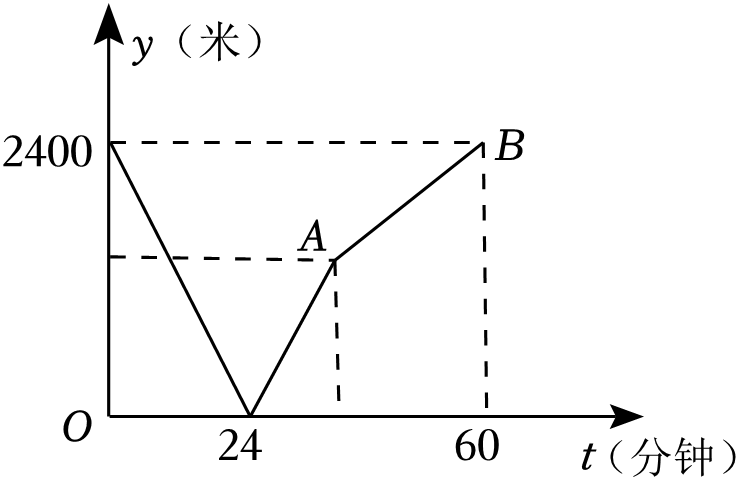 (1)、根据图象信息,求出甲和乙的速度各为多少?(单位:米/分钟)(2)、求线段AB所在的直线的函数表达式;(3)、在整个过程中,请通过计算,t为何值时两人相距400米?25. 如图“字形” , ,
(1)、根据图象信息,求出甲和乙的速度各为多少?(单位:米/分钟)(2)、求线段AB所在的直线的函数表达式;(3)、在整个过程中,请通过计算,t为何值时两人相距400米?25. 如图“字形” , , (1)、作的角平分线 , 交于点 , 作出线段的中点 . (要求:尺规作图,保留作图痕迹,不必写出作法)(2)、利用三角尺过点作 , 垂足为 , 以为圆心,长为半径作圆.
(1)、作的角平分线 , 交于点 , 作出线段的中点 . (要求:尺规作图,保留作图痕迹,不必写出作法)(2)、利用三角尺过点作 , 垂足为 , 以为圆心,长为半径作圆.①判断与直线的位置关系,并说明理由;
②连接 , 若 , , 求的半径.
26. 已知二次函数 .(1)、若它的图象经过点 , 求该函数的对称轴.(2)、若时,y的最小值为1,求出t的值.(3)、如果 , 两点都在这个二次函数的图象上,直线与该二次函数交于 , 两点,则是否为定值?若是,请求出该定值:若不是,请说明理由.27. “转化”是解决数学问题的重要思想方法,通过构造图形全等或者相似建立数量关系是处理问题的重要手段.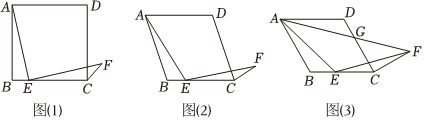 (1)、【问题情景】:如图 , 正方形中,点是线段上一点不与点、重合 , 连接将绕点顺时针旋转得到 , 连接 , 求的度数.
(1)、【问题情景】:如图 , 正方形中,点是线段上一点不与点、重合 , 连接将绕点顺时针旋转得到 , 连接 , 求的度数.以下是两名同学通过不同的方法构造全等三角形来解决问题的思路,
①小聪:过点作的延长线的垂线;
②小明:在上截取 , 使得;
请你选择其中一名同学的解题思路,写出完整的解答过程.
(2)、【类比探究】:如图点是菱形边上一点不与点、重合 , , 将绕点顺时针旋转得到 , 使得 , 则的度数为用含的代数式表示 .(3)、【学以致用】:如图 , 在的条件下,连结 , 与相交于点 , 当时,若 , 求的值.