山东省济宁市嘉祥县2022-2023学年八年级下学期数学期中考试试卷
试卷更新日期:2024-05-08 类型:期中考试
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
-
1. 下列正确的是( )A、 B、 C、 D、2. 在中, , 点 , 分别为 , 的中点,则( )A、 B、 C、 D、3. 下列各组数中,不能构成直角三角形的是( )A、 , , B、 , , C、 , , D、 , ,4. 将整体一分为二,当较大部分与整体部分的比值等于时被公认为是最能引起美感的黄金分割,下列估算正确的是( )A、 B、 C、 D、5. 下列命题中,是真命题的有( )
①对角线相等且互相平分的四边形是矩形②对角线互相垂直的四边形是菱形③四边相等的四边形是正方形④四边相等的四边形是菱形
A、①② B、①④ C、②③ D、③④6. 若顺次连接四边形ABCD各边的中点所得的四边形是菱形,则四边形ABCD的两条对角线AC,BD一定是( )A、互相平分 B、互相平分且相等 C、互相垂直 D、相等7. 如图,九章算术中的“折竹抵地”问题:今有竹高一丈,末折抵地,去根六尺,问折高者几何?意思是:一根竹子,原高一丈一丈十尺 , 一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部尺远,求折断处离地面的高度.设竹子折断处离地面尺,根据题意,可列方程为( ) A、 B、
A、 B、
C、 D、8. 如图,三角形纸片ABC中,∠BAC=90°,AB=2,AC=3.沿过点A的直线将纸片折叠,使点B落在边BC上的点D处;再折叠纸片,使点C与点D重合,若折痕与AC的交点为E,则AE的长是( ) A、 B、 C、 D、9. 如图,在边长为2的等边三角形ABC的外侧作正方形ABED,过点D作DF⊥BC,垂足为F,则DF的长为( )
A、 B、 C、 D、9. 如图,在边长为2的等边三角形ABC的外侧作正方形ABED,过点D作DF⊥BC,垂足为F,则DF的长为( ) A、2+2 B、5- C、3- D、+110. 如图,在四边形ABCD中,∠A=∠B=90°,AD=10cm,BC=8cm,点P从点D出发,以1cm/s的速度向点A运动,点M从点B同时出发,以相同的速度向点C运动,当其中一个动点到达端点时,两个动点同时停止运动.设点P的运动时间为t(单位:s),下列结论正确的是 ( )
A、2+2 B、5- C、3- D、+110. 如图,在四边形ABCD中,∠A=∠B=90°,AD=10cm,BC=8cm,点P从点D出发,以1cm/s的速度向点A运动,点M从点B同时出发,以相同的速度向点C运动,当其中一个动点到达端点时,两个动点同时停止运动.设点P的运动时间为t(单位:s),下列结论正确的是 ( ) A、当 t=4s 时,四边形 ABMP 为矩形 B、当 t=5s 时,四边形 CDPM 为平行四边形 C、当 CD=PM 时,t=4s D、当 CD=PM 时,t=4s 或6s
A、当 t=4s 时,四边形 ABMP 为矩形 B、当 t=5s 时,四边形 CDPM 为平行四边形 C、当 CD=PM 时,t=4s D、当 CD=PM 时,t=4s 或6s二、填空题:本题共5小题,每小题3分,共15分。
-
11. 如图所示的四边形 , 若 , , 则的长度是 .
 12. 小明钉了一个长与宽分别为厘米和厘米的长方形木框,为了增加其稳定性,他准备沿长方形的对角线钉上一根木条,这根木条的长应为厘米.13. 如图,平行四边形中,的平分线交于 , , , 则的长是 .
12. 小明钉了一个长与宽分别为厘米和厘米的长方形木框,为了增加其稳定性,他准备沿长方形的对角线钉上一根木条,这根木条的长应为厘米.13. 如图,平行四边形中,的平分线交于 , , , 则的长是 . 14. 如图,菱形的对角线相交于点O,点E在上,连接 , 点F为的中点,连接 , 若 , , , 则线段的长为 .
14. 如图,菱形的对角线相交于点O,点E在上,连接 , 点F为的中点,连接 , 若 , , , 则线段的长为 .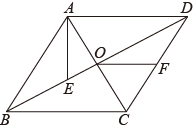 15. 将一组数 , , , , , , 按下列方式进行排列:
15. 将一组数 , , , , , , 按下列方式进行排列:
, , , ;
, , , ;
若的位置记为 , 的位置记为 , 的位置记为 , 则的位置记为 .三、解答题:本题共7小题,共55分。解答应写出文字说明,证明过程或演算步骤。
-
16. 计算:
(1)、;
(2)、 .17. 如图,已知中 , , , 求的面积. 18. 已知:如图,在平行四边形中,点、为对角线上两点,且求证: .
18. 已知:如图,在平行四边形中,点、为对角线上两点,且求证: . 19. 如图所示,四边形ABCD中,AB=3cm,AD=4cm,BC=13cm,CD=12cm,∠A=90°,求四边形ABCD的面积.
19. 如图所示,四边形ABCD中,AB=3cm,AD=4cm,BC=13cm,CD=12cm,∠A=90°,求四边形ABCD的面积.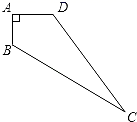 20. 如图是的正方形网格,请仅用无刻度的直尺按要求完成以下作图(保留作图痕迹).
20. 如图是的正方形网格,请仅用无刻度的直尺按要求完成以下作图(保留作图痕迹).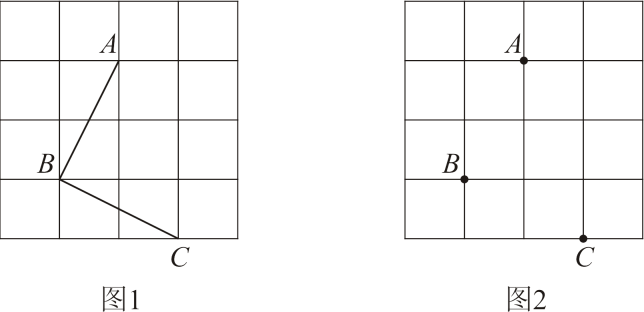 (1)、在图1中作的角平分线;(2)、在图2中过点C作一条直线l,使点A,B到直线l的距离相等.
(1)、在图1中作的角平分线;(2)、在图2中过点C作一条直线l,使点A,B到直线l的距离相等.

