山东省青岛市市南区2023-2024学年七年级下学期数学期中考试试卷
试卷更新日期：2024-05-08 类型：期中考试
一、选择题：本题共8小题，每小题3分，共24分。在每小题给出的选项中，只有一项是符合题目要求的.
-
1. 已知某种新型感冒病毒的直径为0.000000823米，将0.000000823用科学记数法表示为（ ）A、8.23×10﹣6 B、8.23×10﹣7 C、8.23×106 D、8.23×1072. 若∠1与∠2互为余角，∠1与∠3互为补角，则下列选项，错误的是（ ）A、∠3+∠1＝180° B、∠3﹣∠2＝90° C、∠3+∠2＝270°﹣2∠1 D、∠1+∠2＝180°3. 如图，直线c与直线a，b都相交， ， 若平分 ， ， 则的度数为（ ）
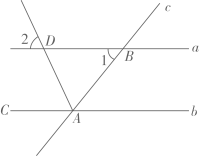A、50° B、65° C、70° D、80°4. 用一定长度的铁丝围成一个长方形，则有下列说法：①长方形的长和宽是两个变量；
②长方形的周长是自变量时，它的宽是因变量；
③长方形的长是自变量时，它的宽是因变量；
④长方形的宽是自变量时，它的长是因变量；
⑤长方形的长是自变量时，它的面积是因变量．
其中正确的说法有（ ）
A、2个 B、3个 C、4个 D、5个5. 下列图形中，线段AD的长表示点A到直线BC距离的是（ ）A、
B、
C、
D、
6. 已知M＝2x2+x﹣6，N＝x2﹣x﹣7，则M、N的大小关系是（ ）A、M＝N B、M≥N C、M≤N D、不能确定7. 观察下面一组数：﹣1，2，﹣3，4，﹣5，6，﹣7，…，将这组数排成如图的形式，按照如图规律排下去，则第10行中从左边数第9个数是（ ）
A、﹣90 B、90 C、﹣91 D、918. 如图，AB∥CD ， OE平分∠BOC ， OF⊥OE ， OP⊥CD ， ∠ABO＝40°，则下列结论：①∠BOE＝70°②OF平分∠BOD ③∠POE＝∠BOF④∠POB＝2∠DOF
其中正确的结论的个数为（ ）
A、4 B、3 C、2 D、1二、填空题：本题共8小题，每小题3分，共24分。
-
9. 计算：＝ ．10. 如图，已知a∥b ， 一块含30°角的直角三角板如图所示放置，∠2＝45°，则∠1等于度．
11. 如图，一块长为a m ， 宽为b m的长方形土地的周长为16m ， 面积为15m2 ， 现将该长方形土地的长、宽都增加2m ， 则扩建后的长方形土地的面积是 ．
12. 如图，将长方形纸片ABCD ， 沿折痕MN折叠，A ， B分别落在对应位置A1 ， B1处，A1B1交AD于点E ， 若∠BNM＝70°，则∠A1ME为 ．
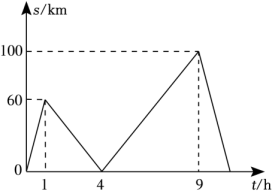
13. 化简：6（7+1）（72+1）（74+1）（78+1）（716+1）+1= ．14. 如图，点E在AC的延长线上，对于给出的四个条件：（1）∠3=∠4；（2）∠1=∠2；（3）∠A=∠DCE；（4）∠D+∠ABD=180°.能判断AB∥CD的有个.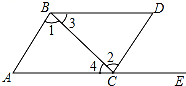
15. A，B两地相距 ， 甲、乙两辆汽车从A地出发到B地，均匀速行驶，甲出发1小时后，乙出发沿同一路线行驶，设甲、乙两车相距s（km），甲行驶的时间为t（h），s与t的关系如图所示，下列说法：①甲车行驶的速度是60km/h，乙车行驶的速度是80km/h；
②甲出发4h后被乙追上；
③甲比乙晚到h；
④甲车行驶8h或h，甲，乙两车相距80km；
其中正确的是 ．
16. 在2024年迎新联欢会上，数学老师和同学们做了一个游戏．她在A ， B ， C三个盘子里分别放了一些小球，小球数依次为a0 ， b0 ， c0 ， 记为G0＝（a0 ， b0 ， c0）．游戏规则如下：三个盘子中的小球数a0≠b0≠c0 ， 则从小球最多的一个盘子中拿出两个，给另外两个盘子各放一个，记为一次操作；n次操作后的小球数记为Gn＝（an ， bn ， cn）．若G0＝（4，6，17），则G3＝ ， G2024＝ ．三、作图题
-
17. 在下列图形中，按要求画出AD ， 使得AD⊥BC ， 交BC于点D ．
(1)、如图①，所有小正方形边长都为1，点A、B、C均在格点上，用无刻度直尺画AD；(2)、如图②，已知“三角形内角和为180°”，用无刻度直尺与圆规作AD（不写作法，保留作图痕迹）．四、计算题：本大题共1小题，共19分。
-
18. 计算与化简(1)、计算：（2x2y）3（﹣4xy2）(2)、计算：(3)、计算：（x﹣2y+4）（x+2y﹣4）(4)、运用乘法公式简便运算：2012×2018﹣20152(5)、先化简，再求值：[（x+y）2﹣y（2x+y）﹣8xy]÷2x ， 其中x＝2，y＝
五、解答题：本题共6小题，共48分。解答应写出文字说明，证明过程或演算步骤。
-
19. 填空，并在括号里注明理由：
如图，已知点O ， E在直线AB上，OD是∠BOC的平分线，过点E作OD的平行线交OC于点F ， 试说明：∠1＝∠2．
说明：∵EF∥OD ，
∴∠3＝∠ ▲ （ ）．
∵EF∥OD ，
∴∠4＝∠ ▲ （ ）．
∵OD是∠BOC的平分线，
∴∠3＝∠4（ ）．
∴∠5＝∠6，
∵∠5+∠1＝180°，∠6+∠2＝180°，
∴∠1＝∠2（ ）．
20. 对于一个图形，通过两种不同的方法计算它的面积，可以得到一个数学等式。例如图1可以得到(a+b)2 =a2 +2ab+b2 ， 请解答下列问题：
(1)、图2所表示的数学等式为(2)、利用(1)得到的结论，解决问题：若a+b+c=12，a2+b2+c2 =60，求ab+ac+bc的值；(3)、如图3，将两个边长分别为a和b的正方形拼在一起，B，C，D三点在同一直线上，连接AE、EG，若两正方形的边长满足a+b=15，ab=35，求阴影部分面积．21. 如图，已知∠1＝∠BDC ， ∠2+∠3＝180°．
(1)、问AD与CE平行吗？如果平行请说明理由．(2)、若CE⊥AE于E ， DA平分∠BDC ， ∠FAB＝68°，求∠1的度数．22. 为了节约用水，某市居民生活用水按级收费，下面是东东家收到的自来水公司水费专用发票．结合发票中的信息回答下列问题．自来水公司水费专用发票发票联
计费日期：2018.9.1﹣﹣2018.10.1
上期抄表数
本期抄表数
本期用水量
587
632
45
自来水费（含污水处理费）
用水量（吨）
单价（元/吨）
金额（元）
第一级：20
第二级：20
第三级：5
2.5
3.45
6.3
50
69
31.5
本期实付金额（大写）：壹佰伍拾元伍角整 小写金额：150.5元
备注：第一级为月用水量20吨及以下（含20吨）；
第二级为月用水量超过20吨，不超过40吨；
第三级为月用水量40吨以上（不含40吨）．
(1)、东东家5月份的用水量为15吨，则这个月的水费为多少？(2)、东东家7月份的用水量为a吨，且达到第三级的用水量，请用含a的整式表示他家7月份的水费；(3)、东东家的11月份的用水量少于10月份，且这两个月的用水量均没到第三级，若这两个月总用水42吨，共缴水费108.8元，分别求东东家这两个月的用水量．23. 【知识回顾】我们在学习代数式求值时，遇到这样一类题：代数式ax﹣y+6+3x﹣5y﹣1的值与x的取值无关，求a的值．
通常的解题思路是：把x、y看作字母，a看作系数，合并同类项．因为代数式的值与x的取值无关，所以含x项的系数为0．
具体解题过程是：原式＝（a+3）x﹣6y+5，
∵代数式的值与x的取值无关，
∴a+3＝0，解得a＝﹣3．
(1)、【理解应用】若关于x的多项式m（2x﹣3）+2m2﹣4x的值与x的取值无关，求m值；
(2)、已知A＝（2x+1）（x﹣2）﹣x（1﹣3m），B＝﹣x2+mx﹣1，且A+2B的值与x的取值无关，求m的值；(3)、【能力提升】7张如图1的小长方形，长为a ， 宽为b ， 按照图2方式不重叠地放在大长方形ABCD内，大长方形中未被覆盖的两个部分都是长方形．设右上角的面积为S1 ， 左下角的面积为S2 ， 当AB的长变化时，S1﹣S2的值始终保持不变，求a与b的等量关系．
24. 已知直线MN∥PQ ， 点A在直线MN上，点B、C为平面内两点，AC⊥BC于点C ．
（1）如图1，当点B在直线MN上，点C在直线MN上方时，延长CB交直线PQ于点D ， 则∠CAB和∠CDP之间的数量关系是____．(1)、如图2，当点C在直线MN上且在点A左侧，点B在直线MN与PQ之间时，过点B作BD⊥AB交直线PQ于点D ． 为探究∠ABC与∠BDP之间的数量关系，小明过点B作BF∥MN ． 请根据他的思路，写出∠ABC与∠BDP的关系，并说明理由；(2)、如图3，在（2）的条件下，作∠ABD的平分线交直线MN于点E ， 当∠AEB＝2∠ABC时，直接写出∠ABC的度数．(3)、如图4，当点C在直线MN上且在点A左侧，点B在直线PQ下方时，过点B作BD⊥AB交直线PQ于点D ． 作∠ABD的平分线交直线MN于点E ， 当∠BDP＝2∠BEN时，请补充图形并直接写出∠ABC的度数．
-
-