湖北省黄石市2023-2024学年八年级下学期数学月考试卷

试卷更新日期：2024-05-08 类型：月考试卷

进入出卷网下载

一、单选题

1. 下列各式中，一定是二次根式的是（）

A、 $\sqrt{a}$ B、 $\sqrt[3]{6}$ C、 $\sqrt{a^{2} + 1}$ D、 $\sqrt{- 2}$

查看试题解析
2. 如图，在 $△ A B C$ 中， $∠ C = 90 °$ ，若 $A C = 1$ ， $A B = 2$ ，则BC的长是（）

A、1 B、 $\sqrt{3}$ C、2 D、 $\sqrt{5}$

查看试题解析
3. 下列式子中，为最简二次根式的是（）

A、 $\sqrt{\frac{1}{2}}$ B、 $\sqrt{3}$ C、 $\sqrt{4}$ D、 $\sqrt{12}$

查看试题解析
4. 下列长度的三条线段能组成直角三角形的是（）

A、4，5，6 B、2，3，4 C、1，1， $\sqrt{2}$ D、1，2，2

查看试题解析
5. 下列运算正确的是（）

A、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ B、 $2 \sqrt{2} - \sqrt{2} = 1$ C、 $\sqrt{2} \times 2 \sqrt{2} = 3 \sqrt{2}$ D、 $\sqrt{8} \div \sqrt{2} = 2$

查看试题解析
6. 以直角三角形的三边为边做正方形，三个正方形的面积如图，正方形A的面积为（）

A、6 B、36 C、64 D、8

查看试题解析
7. 已知 $\sqrt{x - 3} + \sqrt{3 - x} + y = 3$ ，则 $\sqrt{2 x y}$ 的值为（）

A、 $2 \sqrt{3}$ B、 $3 \sqrt{2}$ C、12 D、18

查看试题解析
8. 如图的数轴上，点 $A$ ， $C$ 对应的实数分别为1，3，线段 $A B ⊥ A C$ 于点 $A$ ，且 $A B$ 长为1个单位长度.若以点 $C$ 为圆心， $B C$ 长为半径的弧交数轴于0和1之间的点 $P$ ，则点 $P$ 表示的实数为（）

A、 $3 - \sqrt{5}$ B、 $\sqrt{5} - 2$ C、 $\sqrt{5} - 1$ D、 $3 - \sqrt{10}$

查看试题解析
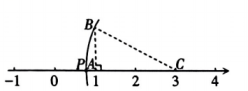9. 勾股定理是人类数学文化的一颗璀璨明珠，是用代数思想解决几何问题最重要的工具，也是数形结合的纽带之一.如图，踏板离地的垂直高度 $B E = 1 m$ ，将它往前推 $4 m$ 至C处时（即水平距离 $C D = 4 m$ ），踏板离地的垂直高度 $C F = 3 m$ ，它的绳索始终拉直，则绳索 $A C$ 的长是( )

A、 $4 m$ B、 $5 m$ C、 $6 m$ D、 $8 m$

查看试题解析
10. 若二次根式 $\sqrt{2 - m}$ 有意义，且关于x的分式方程 $\frac{m}{1 - x}$ +2＝ $\frac{3}{x - 1}$ 有正数解，则符合条件的整数m的和是（）

A、﹣7 B、﹣6 C、﹣5 D、﹣4

查看试题解析

二、填空题

11. 已知式子 $\sqrt{1 - x}$ 有意义，则 $x$ 的取值范围是

查看试题解析
12. 计算： $\sqrt{75} - \sqrt{27} =$ .

查看试题解析
13. 如图，某自动感应门的正上方A处装着一个感应器，离地 $A B = 2.5$ 米，当人体进入感应器的感应范围内时，感应门就会自动打开.一个身高1.6米的学生 $C D$ 正对门，缓慢走到离门1.2米的地方时（ $B C = 1.2$ 米），感应门自动打开，则 $A D =$ 米.

查看试题解析
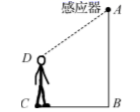14. 同一地点从高空中自由下落的物体，其落到地面所需的时间与物体的质量无关，只与该物体的高度有关.若物体从离地面为h（单位：m）的高处自由下落，落到地面所用的时间为t（单位：s），且t与h的关系可以表示为 $t = \sqrt{\frac{h}{k}}$ （k为常数），当 $h = 80$ 时， $t = 4$ .则从高度为100m的空中自由下落的物体，其落到地面所需的时间为s.

查看试题解析
15. 如图， $△ A B C$ 中， $A B = A C = 5$ ， $B C = 6$ ，点D是AB边上的一个动点，则线段CD的最小值为.

查看试题解析

三、解答题

16. 计算：

(1)、 $\sqrt{12} - 3 \sqrt{\frac{1}{3}} + | \sqrt{3} - 2 |$ ；

(2)、 $\sqrt{48} \div \sqrt{2} - \sqrt{\frac{1}{2}} \times \sqrt{12} + \sqrt{54}$ ；

(3)、 $(\sqrt{3} + \sqrt{2}) (\sqrt{3} - \sqrt{2}) + {(\sqrt{5} - 1)}^{2}$ .

查看试题解析
17. 如图，在4×4的正方形网格中，每个小正方形的边长均为1，每个小正方形的顶点叫做格点.

(1)、在图1中以格点为顶点画△ABC，使△ABC的三边长分别为3、4、5；

(2)、在图2中以格点为顶点画△DEF，使△DEF的三边长分别为 $\sqrt{5}$ 、 $\sqrt{10}$ 、 $\sqrt{13}$ .

查看试题解析
18.

(1)、已知： $x = 2 - \sqrt{3}$ ， $y = 2 + \sqrt{3}$ ，求 $x^{2} + y^{2} - 3 x y$ 的值；

(2)、若 $x = \sqrt{2} + 1$ ，求代数式 $x^{2} - 2 x + 2023$ 的值.

查看试题解析
19. 如图，四边形ABCD中， $∠ B = 90 °$ ， AC为对角线， $D E ⊥ A C$ 于E ， $A B = 8$ ， $B C = 6$ ， $C D = 2 \sqrt{15}$ ， $A D = 2 \sqrt{10}$ .

(1)、求证： $∠ A D C = 90 °$ ；

(2)、求线段DE的长.

查看试题解析
20. 先化简，再求值： $(a - 1 + \frac{2}{a + 1}) \div (a^{2} + 1)$ ，其中 $a = \sqrt{5} - 1$ .

查看试题解析
21. “儿童散学归来早，忙趁东风放纸再”.又到了放风筝的最佳时节.某校八年级（1）班的小明和小亮学习了“勾股定理”之后，为了测得风箏的垂直高度 $C E$ ，他们进行了如下操作：①测得水平距离 $B D$ 的长为 $15$ 米；②根据手中剩余线的长度计算出风箏线 $B C$ 的长为 $25$ 米；③牵线放风筝的小明的身高为 $1.6$ 米.

(1)、求风筝的垂直高度 $C E$ ；

(2)、如果小明想风筝沿 $C D$ 方向下降 $12$ 米，则他应该往回收线多少米？

查看试题解析
22. 数学老师在课堂上提出一个问题：“通过探究知道： $\sqrt{2} \approx 1.414 ⋯$ ，它是无限不循环小数，也叫无理数，它的整数部分是1，那么有谁能说出它的小数部分是多少”，王英举手回答：它的小数部分我们无法全部写出来，但可以用 $\sqrt{2} - 1$ 来表示它的小数部分，张老师夸奖王英真聪明，肯定了她的说法.现请你根据王英的说法解答下列问题：

(1)、请表示出 $\sqrt{7}$ 的小数部分；

(2)、若a为 $\sqrt{6}$ 的小数部分，b为 $\sqrt{5}$ 的整数部分，求 $a + b + \sqrt{24}$ 的值；

(3)、已知 $6 + \sqrt{13} = x + y$ ，其中x是一个正整数， $0 < y < 1$ ，求 $(x + 3 y)^{2}$ 的值.

查看试题解析
23.

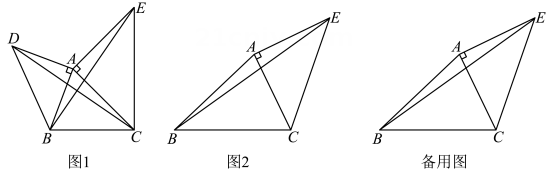(1)、如图1，已知 $△ A B C$ ，以AB、AC为边分别向外作等腰直角三角形ABD和等腰直角三角形ACE ，连接BE、CD.猜想BE与CD有什么数量关系？并说明理由.

(2)、在幸福村的休闲广场上种有四棵景观树，在如图2所示A、B、C、E的位置，数学兴趣小组的同学测得 $∠ A B C = 45 °$ ， $A B = 40 \sqrt{2}$ 米， $B C = 60$ 米.
①求A、C两棵树之间的距离；（结果保留根号）
②如果 $A E = A C$ ，且 $∠ E A C = 90 °$ ，求B、E两棵树之间的距离.

查看试题解析
24. 如图，在平面直角坐标系中， $A (0, a)$ 为y轴正方向上一点， $B (b, 0)$ 为x轴正方向上一点，且满足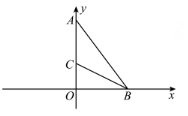 $\sqrt{a - 8} + {(b - 6)}^{2} = 0$ .

(1)、求线段AB的长；

(2)、点C是线段AC上一点，如果BC平分 $∠ A B O$ ，求点C的坐标；

(3)、点P是x轴上一动点，且 $△ P A B$ 为等腰三角形，直接写出所有符合条件的点P的坐标.

查看试题解析