湖北省黄石市大冶市2023-2024学年七年级下学期数学期中试题
试卷更新日期:2024-05-08 类型:期中考试
一、选择题(本大题共10个小题,每小题3分,共30分)
-
1. 现实世界中,平移现象无处不在,中国的方块字中有些也具有平移性,下列汉字是由平移构成的是( )A、
 B、
B、 C、
C、 D、
D、
-
2. 下列图中和是对顶角的是( )A、
 B、
B、 C、
C、 D、
D、
-
3. 实数4的平方根是( )A、 B、±4 C、4 D、±2
-
4. 点M在第二象限,距离x轴5个单位长度,距离y轴3个单位长度,则M点的坐标为( )A、 B、 C、 D、
-
5. 如图,是一局象棋残局,若表示棋子“炮”和“車”的点的坐标分别为 , , 则表示棋子“馬”的点的坐标为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
6.如图所示,把一个长方形纸片沿EF折叠后,点D、C分别落在D'、C'的位置.若∠AED'=50°,则∠EFC等于( )
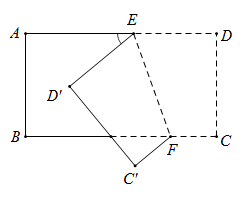 A、 B、 C、 D、
A、 B、 C、 D、 -
7. 如图,在下列条件中,能够证明AD∥CB的条件是( )
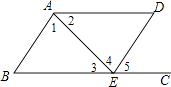 A、∠1=∠4 B、∠B=∠5 C、∠1+∠2+∠D=180° D、∠2=∠3
A、∠1=∠4 B、∠B=∠5 C、∠1+∠2+∠D=180° D、∠2=∠3 -
8. 如图,已知AB∥DE , ∠ABC=80°,∠CDE=140°,则∠C=( )
 A、50° B、40° C、30° D、20°
A、50° B、40° C、30° D、20° -
9. 已知点 , , 将线段平移至 , 点A的对应点在y轴上,点的对应点在x轴上,点的纵坐标为a , 点的横坐标为b , 则的值为( )A、 B、 C、 D、
-
10. 已知x , y是有理数,且 , 则的立方根为( )A、2 B、 C、4 D、
二、填空题(本大题共5个小题,每小题3分,共15分)
-
11. 已知点A(a-2,a)在y轴上,则A点坐标为 .
-
12. 下列五个实数: , , , , 0.101001000100001…,其中无理数的有个.
-
13. 9的算术平方根是 .
-
14. 如图,两个直角三角形重叠在一起,将其中一个三角形沿着点B到点C的方向平移到的位置, , , , 平移距离为5,求阴影部分的面积为 .

-
15. 如图,在平面直角坐标系中,一动点从原点O出发,按向上,向右,向下,向右的方向不断地移动,每次移动一个单位,得到点 , , , , …,那么点(n为自然数)的坐标为 .

三、解答题(本大题共9个小题,共75分)
-
16. 化简与求值:(1)、;(2)、求x的值: .
-
17. 如图,直线、相交于点O , , 平分 .
 (1)、若 , 求的度数;(2)、若 , 求的度数.
(1)、若 , 求的度数;(2)、若 , 求的度数. -
18. 已知的平方根是 , 的立方根是2, .(1)、求a、b、c的值;(2)、求的算术平方根.
-
19. 完成下面的证明:
已知:如图, , 、分别是、的角平分线,求证: .

证明:∵ , ∴(_▲_).
∴(_▲_).
∵、分别是、的角平分线,
∴(_▲_),(_▲_).
∴ .
∴_▲__▲_(_▲_).
∴(_▲_).
-
20. 如图,三角形是由三角形经过某种平移得到的,点A与点 , 点B与点 , 点C与点分别对应,且这六个点都在格点(小正方形的顶点)上,观察各点以及各点坐标之间的关系,解答下列问题:
 (1)、分别写出点B和点的坐标,并说明三角形是由三角形经过怎样的平移得到的.(2)、若是三角形内一点,它随三角形按(1)中方式平移后得到的对应点为 , 分别求a和b的值.(3)、直接写出三角形的面积为 .
(1)、分别写出点B和点的坐标,并说明三角形是由三角形经过怎样的平移得到的.(2)、若是三角形内一点,它随三角形按(1)中方式平移后得到的对应点为 , 分别求a和b的值.(3)、直接写出三角形的面积为 . -
21. 平面直角坐标系中,对于P、Q两点给出定义:若点P到x轴、y轴的距离之差的绝对值等于点Q到x轴、y轴的距离之差的绝对值,则称P、Q两点互为“等差点”,例如,点到x轴、y轴的距离之差的绝对值等于1,点到x轴、y轴的距离之差的绝对值等于1,则P与Q互为“等差点”.
完成问题:
(1)、已知点 , 请写出点A的等差点,他们分别是 . (要求写出两个).(2)、若点与点互为“等差点”,求点N的坐标. -
22. 已知,如图,于延长线交于 , 于延长线交于 , , , .
 (1)、求证:;(2)、求的度数.
(1)、求证:;(2)、求的度数. -
23. 阅读下面的文字,解答问题:
大家知道是无理数,而无理数是无限不循环小数,因此的小数部分我们不可能全部地写出来,于是小明用来表示的小数部分,你同意小明的表示方法吗?
事实上,小明的表示方法是有道理的,因为的整数部分是1,将这个数减去其整数部分,差就是小数部分.
又例如:∵ , 即 , ∴的整数部分为2,小数部分为 .
根据以上提示回答下列问题:
(1)、如图,数轴上点A、B、O、C、D分别表示数 , , 0,1,2,则表示数的点P应落在____. A、线段上 B、线段上 C、线段上 D、线段上(2)、如果的整数部分为a , 的小数部分为b , 求的立方根;(3)、若 , 其中x是整数,且 , 求的平方根.
A、线段上 B、线段上 C、线段上 D、线段上(2)、如果的整数部分为a , 的小数部分为b , 求的立方根;(3)、若 , 其中x是整数,且 , 求的平方根. -
24. 如图①,在平面直角坐标系中, , , 且满足 , 过C作轴于B .
 (1)、求的面积.(2)、在y轴上是否存在点P , 使得的面积等于的面积的?若存在,求出P点坐标;若不存在,请画图并说明理由.(3)、若过B作交y轴于D , 且 , 分别平分 , , 如图②,判断是否为定值,如果是,请求出具体的度数.
(1)、求的面积.(2)、在y轴上是否存在点P , 使得的面积等于的面积的?若存在,求出P点坐标;若不存在,请画图并说明理由.(3)、若过B作交y轴于D , 且 , 分别平分 , , 如图②,判断是否为定值,如果是,请求出具体的度数.
