湖北省宜昌市第五中教联体2023-2024学年七年级下学期期中数学试题
试卷更新日期:2024-05-08 类型:期中考试
一、选择题(共10小题)
-
1. 下列值中,能满足 在实数范围内有意义的是( )A、a=﹣2 B、a=﹣1 C、a=﹣0.0001 D、a=20212. 下列二次根式中,与 的积是无理数的是( )A、 B、 C、 D、3. 下列计算中,正确的是( )A、 ﹣ =1 B、 + = C、 × = D、 ÷ =44. 在▱ABCD中,若∠A:∠B=1:2,则∠A的度数为( )A、30° B、60° C、120° D、150°5. 如图是一个正方形和直角三角形的组合图形,直角三角形的斜边和一条直角边的长分别为10cm,8cm,则该正方形的面积为( )
 A、6cm2 B、36cm2 C、18cm2 D、2cm26. 下列命题的逆命题是假命题的是( )A、全等三角形的对应角相等 B、两直线平行,同位角相等 C、等边三角形三个角相等 D、直角三角形中,斜边的平方等于两直角边的平方和7. 如图,E为正方形ABCD的对角线上一点,四边形EFCG为矩形,若正方形ABCD的边长为4,则EG+GC的长为( )
A、6cm2 B、36cm2 C、18cm2 D、2cm26. 下列命题的逆命题是假命题的是( )A、全等三角形的对应角相等 B、两直线平行,同位角相等 C、等边三角形三个角相等 D、直角三角形中,斜边的平方等于两直角边的平方和7. 如图,E为正方形ABCD的对角线上一点,四边形EFCG为矩形,若正方形ABCD的边长为4,则EG+GC的长为( )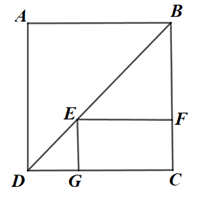 A、4 B、8 C、16 D、328. 如图,在□ABCD中,AB>AD , 按以下步骤作图:以点A为圆心,小于AD的长为半径画弧,分别交AB、AD于点E、F;再分别以点E、F为圆心,大于EF的长为半径画弧,两弧交于点G;作射线AG交CD于点H , 则下列结论中不能由条件推理得出的是( )
A、4 B、8 C、16 D、328. 如图,在□ABCD中,AB>AD , 按以下步骤作图:以点A为圆心,小于AD的长为半径画弧,分别交AB、AD于点E、F;再分别以点E、F为圆心,大于EF的长为半径画弧,两弧交于点G;作射线AG交CD于点H , 则下列结论中不能由条件推理得出的是( ) A、AG平分∠DAB B、AD=DH C、DH=BC D、CH=DH9.
A、AG平分∠DAB B、AD=DH C、DH=BC D、CH=DH9.如图,正方形ABCD的面积为1,则以相邻两边中点连线EF为边正方形EFGH的周长为( )
 A、 B、2 C、 +1 D、2 +110. 在《算法统宗》中有一道“荡秋千”的问题:“平地秋千未起,踏板一尺离地送行二步与人齐,五尺人高曾记.仕女佳人争蹴,终朝笑语欢嬉.良工高士素好奇,算出索长有几.”此问题可理解为:如图,有一架秋千,当它静止时,踏板离地距离长度为1尺.将它往前水平推送10尺时,即=10尺,则此时秋千的踏板离地距离就和身高5尺的人一样高.若运动过程中秋千的绳索始终拉得很直,则绳索长为( )
A、 B、2 C、 +1 D、2 +110. 在《算法统宗》中有一道“荡秋千”的问题:“平地秋千未起,踏板一尺离地送行二步与人齐,五尺人高曾记.仕女佳人争蹴,终朝笑语欢嬉.良工高士素好奇,算出索长有几.”此问题可理解为:如图,有一架秋千,当它静止时,踏板离地距离长度为1尺.将它往前水平推送10尺时,即=10尺,则此时秋千的踏板离地距离就和身高5尺的人一样高.若运动过程中秋千的绳索始终拉得很直,则绳索长为( ) A、13.5尺 B、14尺 C、14.5尺 D、15尺
A、13.5尺 B、14尺 C、14.5尺 D、15尺二、填空题(共5小题)
-
11. 顺次连接一个矩形各边中点得到的四边形是 .12. 将多项式在实数范围内分解因式,则 .13. 已知a是负数,b是正数,化简 , 正确的结果是 .14. 如图,数轴上点A对应的数为2,于A , 且 , 以O为圆心,以为半径画圆,交数轴于点C , 则长为 .
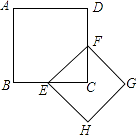
 15. 以正方形的为一边,作等边 , 连接 , 则 .
15. 以正方形的为一边,作等边 , 连接 , 则 .三、解答题(共9小题)
-
16. 计算:.17. 已知 , 且x , y都是正数,求的值.18. 如图,在中,点E , F是对角线上的两点,请添加一个条件,使四边形是平行四边形,并写出证明的过程.
 19. 如图,在△ABC中,AB=13,BC=12,AC=5,点D是BC上一点,且CD=3.
19. 如图,在△ABC中,AB=13,BC=12,AC=5,点D是BC上一点,且CD=3.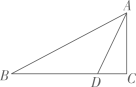 (1)、试判断△ABC的形状,并说明理由;(2)、求AD的长.20. 阅读材料,解答下列问题:
(1)、试判断△ABC的形状,并说明理由;(2)、求AD的长.20. 阅读材料,解答下列问题:材料:已知 , 求的值.
李聪同学是这样解答的:
∵
∴
这种方法称为“构造对偶式”
问题:已知
(1)、求的值;(2)、求的值.21. 研究立体图形问题的基本思路是把立体图形问题转化为平面图形问题.(1)、阅读材料立体图形中既不相交也不平行的两条直线所成的角,就是将直线平移使其相交所成的角.
例如,正方体(图1).因为在平面中, , 与相交于点A , 所以直线与所成的就是既不相交也不平行的两条直线与所成的角.
解决问题
如图1,已知正方体 , 求既不相交也不平行的两条直线与所成角的大小.
 (2)、如图2,M , N是正方体相邻两个面上的点.
(2)、如图2,M , N是正方体相邻两个面上的点.①下列甲、乙、丙三个图形中,只有一个图形可以作为图2的展开图,这个图形是;
②在所选正确展开图中,若点M到 , 的距离分别是2和5,点N到 , 的距离分别是4和3,P是上一动点,求的最小值.
 22.
22.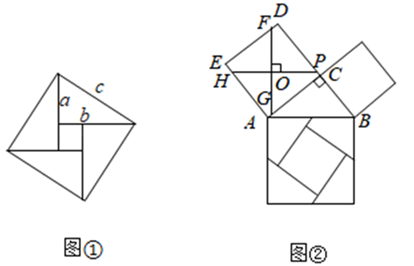 (1)、阅读理解
(1)、阅读理解我国是最早了解勾股定理的国家之一,它被记载于我国古代的数学著作《周髀算经》中.汉代数学家赵爽为了证明勾股定理,创制了一幅如图①所示的“弦图”,后人称之为“赵爽弦图”.根据“赵爽弦图”写出勾股定理和推理过程;
(2)、问题解决勾股定理的证明方法有很多,如图②是古代的一种证明方法:过正方形ACDE的中心O,作FG⊥HP,将它分成4份,所分成的四部分和以BC为边的正方形恰好能拼成以AB为边的正方形.若AC=12,BC=5,求EF的值.
23. 正方形中,点E在边 , 上运动(不与正方形顶点重合).作射线 , 将射线绕点A逆时针旋转 , 交射线于点F . (1)、如图,点E在边上, , 则图中与线段相等的线段是;(2)、过点E作 , 垂足为G , 连接 , 求的度数;24. 综合与实践
(1)、如图,点E在边上, , 则图中与线段相等的线段是;(2)、过点E作 , 垂足为G , 连接 , 求的度数;24. 综合与实践【问题情境】
如图1,小华将矩形纸片先沿对角线折叠,展开后再折叠,使点B落在对角线上,点B的对应点记为 , 折痕与边 , 分别交于点E , F .
 (1)、【活动猜想】
(1)、【活动猜想】如图2,当点与点D重合时,四边形是哪种特殊的四边形?并说明理由.
(2)、【问题解决】如图3,当与满足什么关系时,始终有与对角线平行?请说明理由.
(3)、【深入探究】在(2)的情形下,设与 , 分别交于点O , P , 试探究三条线段 , , 之间满足的等量关系,直接写出答案.