湖北省荆门市京山市2023-2024学年七年级下学期数学期中试题

试卷更新日期：2024-05-08 类型：期中考试

进入出卷网下载

一、选择题（本题共10小题，每小题3分，共30分）

1. 下面四个图形中，∠1与∠2是对顶角的是（　　）

A、 B、 C、 D、

查看试题解析
2. 9的算术平方根是（）

A、 $\pm 3$ B、 $\pm \sqrt{9}$ C、3 D、-3

查看试题解析
3. 如图，小手盖住的点的坐标可能为（）

A、 $(5 ， 2)$ B、 $(- 6 ， 3)$ C、 $(- 4 ， - 6)$ D、 $(3 ， - 4)$

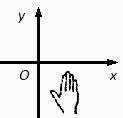查看试题解析
4. 如图，要测量两堵围墙形成的∠AOB的度数，先分别延长AO、BO得到∠COD，然后通过测量∠COD的度数从而得到∠AOB的度数，其中运用的原理是( )

A、对顶角相等 B、同角的余角相等 C、等角的余角相等 D、垂线段最短

查看试题解析
5. 如图， $A B ⊥ A C$ ， $A D ⊥ B C$ ，能够表示点C到直线 $A D$ 的距离的是（）．

A、 $A C$ 的长 B、 $C D$ 的长 C、 $A B$ 的长 D、 $A D$ 的长

查看试题解析
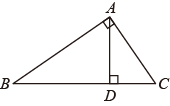6. 如图是小刚画的一张脸，若用点A(1，1)表示左眼的位置，点B(3，1)表示右眼的位置，则嘴巴点C的位置可表示为（）

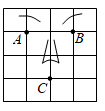A、(2，﹣1) B、(2，1) C、(3，﹣1) D、(2，0)

查看试题解析
7. 下列说法：①5是25的算术平方根；② $\frac{5}{6}$ 是 $\frac{25}{36}$ 的一个平方根；③ ${(- 4)}^{2}$ 的平方根是 $- 4$ ；④0的平方根与算术平方根都是0．其中正确的个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
8. 已知 $\sqrt[3]{0.214} \approx 0.5981$ ， $\sqrt[3]{2.14} \approx 1.289$ ， $\sqrt[3]{21.4} \approx 2.776$ ，则 $\sqrt[3]{21400} \approx$ （）

A、 $27.76$ B、 $12.89$ C、 $59.81$ D、 $5.981$

查看试题解析
9. 将一张长方形纸条ABCD沿EF折叠后，ED交BF于点G ．若∠BGE＝130°，则∠EFC的度数是（　　）

A、110° B、115° C、120° D、125°

查看试题解析
10. 如图，在平面直角坐标系中，一动点从原点O出发，按向上、向右、向下、向右的方向依次平移，每次移动一个单位，得到点 $A_{1} (0 ， 1)$ ， $A_{2} (1 ， 1)$ ， $A_{3} (1 ， 0)$ ， $A_{4} (2 ， 0)$ ， …，那么点 $A_{2023}$ 的坐标为（）

A、 $(1011 ， 0)$ B、 $(1011 ， 1)$ C、 $(1010 ， 0)$ D、 $(1010 ， 1)$

查看试题解析

二、填空题（本题共6小题，每小题3分，共18分）

11. 写出一个比 $- 3$ 大的负无理数．

查看试题解析
12. 点 $A (a - 3, a + 2)$ 在横轴上，则 $a =$ ．

查看试题解析
13. 如图，在一块长为am，宽为bm的长方形草地上，有一条弯曲的小路，小路的左边线向右平移1m就是它的右边线．则这块草地的绿地面积是m² ．

查看试题解析
14. 光线在不同介质中的传播速度不同，因此当光线从水中射向空气时，要发生折射．由于折射率相同，所以在水中平行的光线，在空气中也是平行的．如图，当 $∠ 1 = 45 °$ ， $∠ 2 = 122 °$ 时，则（1） $∠ 6 =$ $°$ ，（2） $∠ 8 =$ $°$ ．

查看试题解析
15. 有一个数值转换器，原理如图：那么输入的x为729时，输出的y是．

查看试题解析

三、解答题（本题共8小题，共72分）

16. 求下列各式中的 $x$ ．

(1)、 ${(x - 1)}^{2} = 4$

(2)、 $x^{3} - 3 = \frac{3}{8}$

查看试题解析
17. 如图．两条直线a ， b相交．

(1)、如果∠1=60°，求∠2，∠3，∠4的度数；

(2)、如果2∠3=3∠1，求∠2，∠3，∠4的度数．

查看试题解析
18. 计算：

(1)、 $(\sqrt{3} + \sqrt{2}) - \sqrt{2}$ ；

(2)、 $\sqrt{3} (\sqrt{3} + \frac{1}{\sqrt{3}}) - \sqrt[3]{1 - \frac{37}{64}}$

查看试题解析
19. 完成下面的证明．

(1)、如图（1），点D ， E ， F分别是三角形ABC的边BC ， CA ， AB上的点， $D E$ // $B A$ ， $D F$ $∥$ $C A$ ．
求证： $∠ F D E = ∠ A$ ．
证明：∵ $D E$ $∥$ $B A$ ，
∴ $∠ F D E =$     ▲    （    ▲    ）
∵ $D F$ $∥$ $C A$ ，
∴ $∠ A =$     ▲    （    ▲    ）
∴ $∠ F D E = ∠ A$ ．（    ▲    ）

(2)、如图（2），AB和CD相交于点O ， $∠ C = ∠ C O A$ ， $∠ D = ∠ B O D$ ．
求证： $A C$ $∥$ $B D$ ．
证明：∵ $∠ C = ∠ C O A$ ， $∠ D = ∠ B O D$ ，
又 $∠ C O A = ∠ B O D$ （    ▲    ）
∴ $∠ C =$     ▲
∴ $A C$ $∥$ $B D$ （    ▲    ）

查看试题解析
20. 在平面直角坐标系中，已知点 $A (- a, 3 a + 2)$ ， $B (1, a - 2)$ ．

(1)、若 $A B ∥ y$ 轴，求点A的坐标；

(2)、若 $A B ∥ x$ 轴，求线段 $A B$ 的长；

(3)、若点B到两坐标轴的距离相等，求a的值；

(4)、若点 $C (1, a + 2) (a > 0)$ ， $△ A B C$ 的面积为8，求点C的坐标．

查看试题解析
21. 如图，已知 $∠ 1 = ∠ B D C$ ， $∠ 2 + ∠ 3 = 180 °$ ．

(1)、请你判断DA与CE的位置关系，并说明理由；

(2)、若DA平分 $∠ B D C$ ， $C E ⊥ A E$ 于点E ， $∠ 1 = 70 °$ ，求 $∠ F A B$ 的度数．

查看试题解析
22. 如图，用两个面积为 $200 c m^{2}$ 的小正方形拼成一个大的正方形．

(1)、则大正方形的边长是；

(2)、若沿着大正方形边的方向裁出一个长方形，能否使裁出的长方形纸片的长宽之比为 $4 : 3$ ，且面积为 $360 c m^{2}$ ？

查看试题解析
23. 如图，在平面直角坐标系中，A（﹣1，﹣2），B（﹣2，﹣4），C（﹣4，﹣1）．

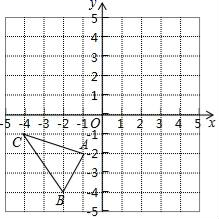(1)、把△ABC向上平移2个单位长度，再向右平移1个单位长度后得到△A₁B₁C₁ ，请画出△A₁B₁C₁ ，并写出点A₁ ， B₁ ， C₁的坐标；

(2)、求△A₁B₁C₁的面积；

(3)、点P在坐标轴上，且△A₁B₁P的面积是2，求点P的坐标．

查看试题解析
24. 如图，直线HD $∥$ GE ，点A在直线HD上，点C在直线GE上，点B在直线DH、GE之间，∠DAB＝120°．

(1)、如图1，若∠BCG＝40°，求∠ABC的度数；

(2)、如图2，AF平分∠HAB ， BC平分∠FCG ， ∠BCG＝20°，比较∠B ， ∠F的大小；

(3)、如图3，点P是线段AB上一点，PN平分∠APC ， CN平分∠PCE ，直接写出∠HAP和∠N的数量关系式．

查看试题解析