2024年中考数学精选压轴题之三角形全等
试卷更新日期:2024-05-08 类型:三轮冲刺
一、选择题
-
1. 如图,在平面直角坐标系中, , 且 , 则点的坐标是( )
 A、 B、 C、 D、2. 如图所示,在四边形中, , 是对角线,是等边三角形, , , , 则的长为.( )
A、 B、 C、 D、2. 如图所示,在四边形中, , 是对角线,是等边三角形, , , , 则的长为.( ) A、 B、 C、 D、3. 如图,正方形的对角线、相交于点O,平分交于点E.过点E作 , 交于点F,若四边形的面积为1,则的长为( )
A、 B、 C、 D、3. 如图,正方形的对角线、相交于点O,平分交于点E.过点E作 , 交于点F,若四边形的面积为1,则的长为( ) A、 B、1 C、 D、24. 如图,是等边内一点, , 将线段以点为旋转中心逆时针旋转得到线段 , 下列结论:①可以由绕点逆时针旋转得到;②点与的距离为6;③;④;⑤ . 其中正确的结论有( )个
A、 B、1 C、 D、24. 如图,是等边内一点, , 将线段以点为旋转中心逆时针旋转得到线段 , 下列结论:①可以由绕点逆时针旋转得到;②点与的距离为6;③;④;⑤ . 其中正确的结论有( )个 A、5 B、4 C、3 D、25. 如图,已知 和 都是等腰三角形, , 交于点F,连接 ,下列结论:① ;② ;③ 平分 ;④ .其中正确结论的个数有( )
A、5 B、4 C、3 D、25. 如图,已知 和 都是等腰三角形, , 交于点F,连接 ,下列结论:① ;② ;③ 平分 ;④ .其中正确结论的个数有( ) A、1个 B、2个 C、3个 D、4个6. 如图,已知△ABC中, , , 三角形的顶点在相互平行的三条直线 , , 上,且 , 之间的距离为1, , 之间的距离为2,则的值是( )
A、1个 B、2个 C、3个 D、4个6. 如图,已知△ABC中, , , 三角形的顶点在相互平行的三条直线 , , 上,且 , 之间的距离为1, , 之间的距离为2,则的值是( ) A、10 B、13 C、20 D、267. 将四个全等的三角形按如图所示的方式围成一个正方形 , 记的面积为 , 四边形的面积为.若 , , , 则图中阴影部分的面积为( )
A、10 B、13 C、20 D、267. 将四个全等的三角形按如图所示的方式围成一个正方形 , 记的面积为 , 四边形的面积为.若 , , , 则图中阴影部分的面积为( )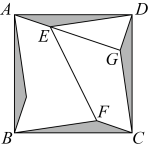 A、 B、 C、 D、8. 如图,正方形 , 点在边上,且 , , 垂足为 , 且交于点 , 与交于点 , 延长至 , 使 , 连接 , 有如下结论:;;; . 上述结论中,正确的个数是( )
A、 B、 C、 D、8. 如图,正方形 , 点在边上,且 , , 垂足为 , 且交于点 , 与交于点 , 延长至 , 使 , 连接 , 有如下结论:;;; . 上述结论中,正确的个数是( ) A、个 B、个 C、个 D、个9. 如图,在等边△PQB中,点A为PQ上一动点(不与P,Q重合),再以AB为边作等边△ABC,连接PC.有以下结论:①PB平分∠ABC;②AQ=CP;③PC//QB;④PB=PA+PC;⑤当 BC⊥BQ时,△ABC的周长最小,其中一定正确的有( )
A、个 B、个 C、个 D、个9. 如图,在等边△PQB中,点A为PQ上一动点(不与P,Q重合),再以AB为边作等边△ABC,连接PC.有以下结论:①PB平分∠ABC;②AQ=CP;③PC//QB;④PB=PA+PC;⑤当 BC⊥BQ时,△ABC的周长最小,其中一定正确的有( )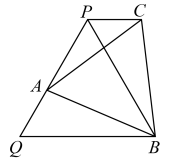 A、①②③ B、②③④ C、③④⑤ D、②③④⑤10. 在Rt△ABC中,∠ACB=90°,AC=BC,D为BC中点,连接AD,过点C作CE⊥AD于点E,交AB于点M.过点B作BF⊥BC交CE的延长线于点F,则下列结论正确的有( )(请填序号)
A、①②③ B、②③④ C、③④⑤ D、②③④⑤10. 在Rt△ABC中,∠ACB=90°,AC=BC,D为BC中点,连接AD,过点C作CE⊥AD于点E,交AB于点M.过点B作BF⊥BC交CE的延长线于点F,则下列结论正确的有( )(请填序号)①△ACD≌△CBF;②∠BDM=∠ADC;③连接AF,则有△ACF是等边三角形;④连接DF,则有AB垂直平分DF.
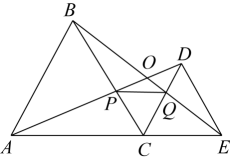
 A、①②③ B、①②④ C、①③④ D、①④11. 如图,C为线段AE上一动点(不与点A , E重合),在AE同侧分别作等边△ABC和等边△ECD , AD与BE交于点O , AD与BC交于点P , BE与CD交于点Q连接PQ . 以下五个结论正确的是( )
A、①②③ B、①②④ C、①③④ D、①④11. 如图,C为线段AE上一动点(不与点A , E重合),在AE同侧分别作等边△ABC和等边△ECD , AD与BE交于点O , AD与BC交于点P , BE与CD交于点Q连接PQ . 以下五个结论正确的是( )① ;②PQ∥AE; ③ ;④ ;⑤
 A、①③⑤ B、①③④⑤ C、①②③⑤ D、①②③④⑤12. 如图,已知 , 点是的平分线上的一上定点,点 , 分别在射线和射线上,且.下列结论:①是等边三角形;②四边形的面积是一个定值;①当时,的周长最小;④当时,也平行于.其中正确的个数是( )
A、①③⑤ B、①③④⑤ C、①②③⑤ D、①②③④⑤12. 如图,已知 , 点是的平分线上的一上定点,点 , 分别在射线和射线上,且.下列结论:①是等边三角形;②四边形的面积是一个定值;①当时,的周长最小;④当时,也平行于.其中正确的个数是( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
13. 如图,在矩形中,是的中点,连接 , 将沿着翻折得到 , 交于点 , 延长 , 相交于点 , 若 , , 则 .
 14. 如图,在中,D为斜边的中点,点E在边上,将沿叠至 . 若的延长线经过点D , 平分 , , 则的值为 , 的长为 .
14. 如图,在中,D为斜边的中点,点E在边上,将沿叠至 . 若的延长线经过点D , 平分 , , 则的值为 , 的长为 . 15. 如图,已知在四边形ABCD内,DB=DC,∠DCA=60°,∠DAC=78°,∠CAB=24°,则∠ACB=.
15. 如图,已知在四边形ABCD内,DB=DC,∠DCA=60°,∠DAC=78°,∠CAB=24°,则∠ACB=.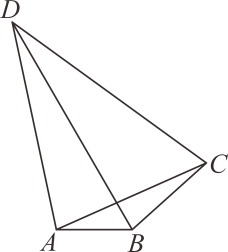 16. 如图,在长方形中, , , 点E为上一点,将沿翻折至 , 延长交于点O , 交的延长线于点G , 且 , 则的长为 .
16. 如图,在长方形中, , , 点E为上一点,将沿翻折至 , 延长交于点O , 交的延长线于点G , 且 , 则的长为 .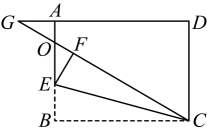 17. 如图,正方形ABCD中,点E.F分别在边BC,CD上,AB=6, , 连接BD交AF于点N,交AE于点M,若 , 则DN为 .
17. 如图,正方形ABCD中,点E.F分别在边BC,CD上,AB=6, , 连接BD交AF于点N,交AE于点M,若 , 则DN为 . 18. 如图, 在 中, 平分 , 点 在 的延长线上, , 若 , 则的度数为 .
18. 如图, 在 中, 平分 , 点 在 的延长线上, , 若 , 则的度数为 .
三、解答题
-
19. 在△ABC中,AC=BC , ∠ACB=90°,D、E是直线AB上两点.∠DCE=45°
 (1)、当CE⊥AB时,点D与点A重合,显然DE2=AD2+BE2(不必证明);(2)、如图,当点D不与点A重合时,求证:DE2=AD2+BE2;(3)、当点D在BA的延长线上时,(2)中的结论是否成立?画出图形,说明理由.20. 在中, , 点为边的中点,点在边上.
(1)、当CE⊥AB时,点D与点A重合,显然DE2=AD2+BE2(不必证明);(2)、如图,当点D不与点A重合时,求证:DE2=AD2+BE2;(3)、当点D在BA的延长线上时,(2)中的结论是否成立?画出图形,说明理由.20. 在中, , 点为边的中点,点在边上. (1)、若 , , 如图 , 求的长;(2)、过点作与边交于点如图 , 试探究:线段、、三者之间的数量关系,并证明你的结论.21. 已知和都是等腰三角形,且 , , 若点D在边上运动时,总保持 , 连接与交于点F .
(1)、若 , , 如图 , 求的长;(2)、过点作与边交于点如图 , 试探究:线段、、三者之间的数量关系,并证明你的结论.21. 已知和都是等腰三角形,且 , , 若点D在边上运动时,总保持 , 连接与交于点F . (1)、①如图1,当点D为边中点时,则的值为 ▲ ;
(1)、①如图1,当点D为边中点时,则的值为 ▲ ;②如图2,当点D不为边中点时,求证:;
(2)、如图3,当点D在边上运动中恰好使得时,若 , , 求的长.22. 中, , , 点是直角边所在直线上一点,连接 , 以为直角边向上作等腰 , , , 过点作 , 垂足为 . (1)、如图1,当点在线段上,且时,请你通过观察、测量、猜想,直接写出;;(2)、如图2,当点在线段的延长线上,且时:
(1)、如图1,当点在线段上,且时,请你通过观察、测量、猜想,直接写出;;(2)、如图2,当点在线段的延长线上,且时:①请你由观察、猜想直接写出_▲_;
②请你规范、严谨的证明: .
(3)、如图3,当点在线段的延长线上,且时,点为线段上任意一点,以为斜边向上做等腰 , , , 连接 , 已知 , 请你直接写出当长度最短时,线段的值为 .23. 如图,在△ABC 和△ADE 中,AB=AD,AC=AE,∠BAC+∠DAE=180°. (1)、如图 1,当点 C 在 AD 上时,∠BAC=90°,连接 CE,若∠ABC=30°,求∠CED 的度数;(2)、如图 2,当点 C 在 AD 上时,∠BAC=90°,延长 BC 交 DE 于 M,连接 AM,求证:AM 平分∠CME;(3)、如图 3,若∠BAC≠90°,连接 BE、CD,F 为 BE 中点,连接 AF,请猜想线段 AF、CD 之间的数量关 系,并证明你的猜想.24. 如图,为的中线,以为直角边在其右侧作直角 , , 与交于点F , .
(1)、如图 1,当点 C 在 AD 上时,∠BAC=90°,连接 CE,若∠ABC=30°,求∠CED 的度数;(2)、如图 2,当点 C 在 AD 上时,∠BAC=90°,延长 BC 交 DE 于 M,连接 AM,求证:AM 平分∠CME;(3)、如图 3,若∠BAC≠90°,连接 BE、CD,F 为 BE 中点,连接 AF,请猜想线段 AF、CD 之间的数量关 系,并证明你的猜想.24. 如图,为的中线,以为直角边在其右侧作直角 , , 与交于点F , . (1)、如图1,若 , 求的长;(2)、如图2,若将绕点C逆时针旋转得到 , 连接、 , 探究、的数量关系,并说明理由;(3)、如图3,若 , , , 直线上有一点M , 连接 , 将沿着翻折到所在的平面内得到 , 取的中点P , 连接 , 当最小时,请直接写出的面积.25. 如图,在四边形ABCD中,∠BAD=120°,∠BCD=60°,AB=AD , BC=DC , 在边BC、DC所在直线上分别有E、F两点,且始终有.
(1)、如图1,若 , 求的长;(2)、如图2,若将绕点C逆时针旋转得到 , 连接、 , 探究、的数量关系,并说明理由;(3)、如图3,若 , , , 直线上有一点M , 连接 , 将沿着翻折到所在的平面内得到 , 取的中点P , 连接 , 当最小时,请直接写出的面积.25. 如图,在四边形ABCD中,∠BAD=120°,∠BCD=60°,AB=AD , BC=DC , 在边BC、DC所在直线上分别有E、F两点,且始终有. (1)、如图1,当E、F在BC、DC上,AE=AF时,求证:BE+DF=EF;(2)、如图2,当E、F在BC、DC上,AE≠AF时,(1)问中的结论是否仍成立请说理;(3)、如图3,当E、F在边BC、DC的延长线上时,直接写出BE、DF、EF之间的数量关系,不必证明.26. 在中, , 点是边上一点,连接 , 过点作直线的垂线,垂足为点
(1)、如图1,当E、F在BC、DC上,AE=AF时,求证:BE+DF=EF;(2)、如图2,当E、F在BC、DC上,AE≠AF时,(1)问中的结论是否仍成立请说理;(3)、如图3,当E、F在边BC、DC的延长线上时,直接写出BE、DF、EF之间的数量关系,不必证明.26. 在中, , 点是边上一点,连接 , 过点作直线的垂线,垂足为点 (1)、如图1,若于点 , 求证:;(2)、如图2,在线段上截取 , 连接交于点 , 求证:;(3)、如图3,若点为的中点,点是线段延长线上的一点,连接 , 求 , , 的数量关系
(1)、如图1,若于点 , 求证:;(2)、如图2,在线段上截取 , 连接交于点 , 求证:;(3)、如图3,若点为的中点,点是线段延长线上的一点,连接 , 求 , , 的数量关系