2024年江苏省南京市中考数学仿真模拟卷

试卷更新日期：2024-05-08 类型：中考模拟

进入出卷网下载

一、选择题（每题2分，共12分）

1. 风云二号是我国自行研制的第一代地球静止气象卫星，它在地球赤道上空距地面约35800公里的轨道上运行．将35800用科学记数法表示应为（）

A、 $0.358 \times 1 0^{5}$ B、 $35.8 \times 1 0^{3}$ C、 $3.58 \times 1 0^{5}$ D、 $3.58 \times 1 0^{4}$

查看试题解析
2. 估计 $\sqrt{6} + 1$ 的值在

A、2到3之间 B、3到4之间 C、4到5之间 D、5到6之间

查看试题解析
3. 如图，若干全等正五边形排成形状，图中所示的是前3个正五边形，则要完成这一圆环还需这样的正五边形（）

A、6个 B、7个 C、9个 D、10个

查看试题解析
4. 二次函数 $y = x^{2} - 2 x - 3$ 的顶点在第几象限（）

A、一 B、二 C、三 D、四

查看试题解析
5. 如图，小聪用图1中的一副七巧板拼出如图2所示“鸟”，已知正方形ABCD的边长为4，则图2中E，F两点之间的距离为（）

A、 $\sqrt{26}$ B、 $2 \sqrt{13}$ C、 $\sqrt{10}$ D、 $\sqrt{16}$

查看试题解析
6. 如图，四个全等的直角三角形排成“赵爽弦图”，其中四边形ABCD与四边形EFGH都是正方形.连结DG并延长，交BC于点 $P$ ，点 $P$ 为BC的中点.若 $E F = 2$ ，则AE的长为（）

A、4 B、 $1 + \sqrt{2}$ C、 $1 + \sqrt{5}$ D、 $\sqrt{3}$

查看试题解析

二、填空题（每题2分，共20分）

7. 写出一个比4小的正无理数．

查看试题解析
8. 要使式子 $\frac{\sqrt{x - 5}}{3}$ 有意义，x的取值范围是．

查看试题解析
9. 计算： $\sqrt{16} \times \sqrt{\frac{1}{2}} + \sqrt{8} =$ ．

查看试题解析
10. 若一元二次方程x²＋x－c＝0没有实数根，则c的取值范围是．

查看试题解析
11. 规定两数a、b之间的一种运算，记作 $(a, b)$ ：如果 $a^{c} = b$ ，那么 $(a, b) = c$ ．例如：因为 $2^{3} = 8$ ，所以 $(2 ， 8) = 3$ ．根据上述规定，填空：若 $(2 ， 10) = x$ ， $(2 ， 5) = y$ ，则 $2^{x^{2} - y^{2}}$ 的值为．

查看试题解析
12. 已知样本x₁ ， x₂ ， …x_n的平均数是5，方差是3，则样本3x₁+5，3x₂+5，…3x_n+5的方差是．

查看试题解析
13. 甲计划用若干个工作日完成某项工作，从第三个工作日起，乙加入此项工作，且甲乙两人工效率相同，结果提前 $4$ 天完成任务，则甲计划完成此项工作的天数是．

查看试题解析
14. 已知点 $(x_{1}, y_{1})$ ， $(x_{2}, y_{2})$ ， $(x_{3}, y_{3})$ 在反比例函数 $y = \frac{k^{2} + 1}{x}$ 的图象上，且 $x_{1} < 0 < x_{2} < x_{3}$ ，则 $y_{1}$ ， $y_{2}$ ， $y_{3}$ 的大小关系是．

查看试题解析
15. 如图， $A B$ 是 $⊙ O$ 的弦， $O A ⊥ O D$ ， $B D$ 与 $⊙ O$ 相切， $A B$ ， $O D$ 相交于点 $C$ ，若 $O A = 3$ ， $O C = 1$ ，则线段 $B D$ 的长为．

查看试题解析
16. 如图，在平面直角坐标系中，点 $A$ ， $B$ ， $C$ 的坐标分别为 $(- 1, 0)$ ， $(0, - 1)$ ， $(2, 0)$ ，点 $E$ 是三角形 $A B C$ 的外接圆 $P$ 上一点， $B E$ 交线段 $A C$ 于点 $D$ ，若 $∠ D B C = 45 °$ ，则点 $D$ 的坐标为.

查看试题解析

三、解答题（共11题，共88分）

17. 解不等式 $\frac{x - 1}{2} \geq \frac{2}{3} x - 1$ ，并把它的解集在数轴上表示出来．

查看试题解析
18. 小红在计算 $(\frac{a}{a - b} - 1) \div \frac{b}{a^{2} - b^{2}}$ 时，解答过程如下：
原式 $= \frac{a - a - b}{a - b} \div \frac{b}{(a + b) (a - b)} ①$
$= \frac{- b}{a - b} \cdot \frac{(a + b) (a - b)}{b} ②$
$= - a - b ③$

(1)、小红的解答从第步开始出错；

(2)、请写出正确的解答过程．

查看试题解析
19. 如图，点D ， E ， F分别是 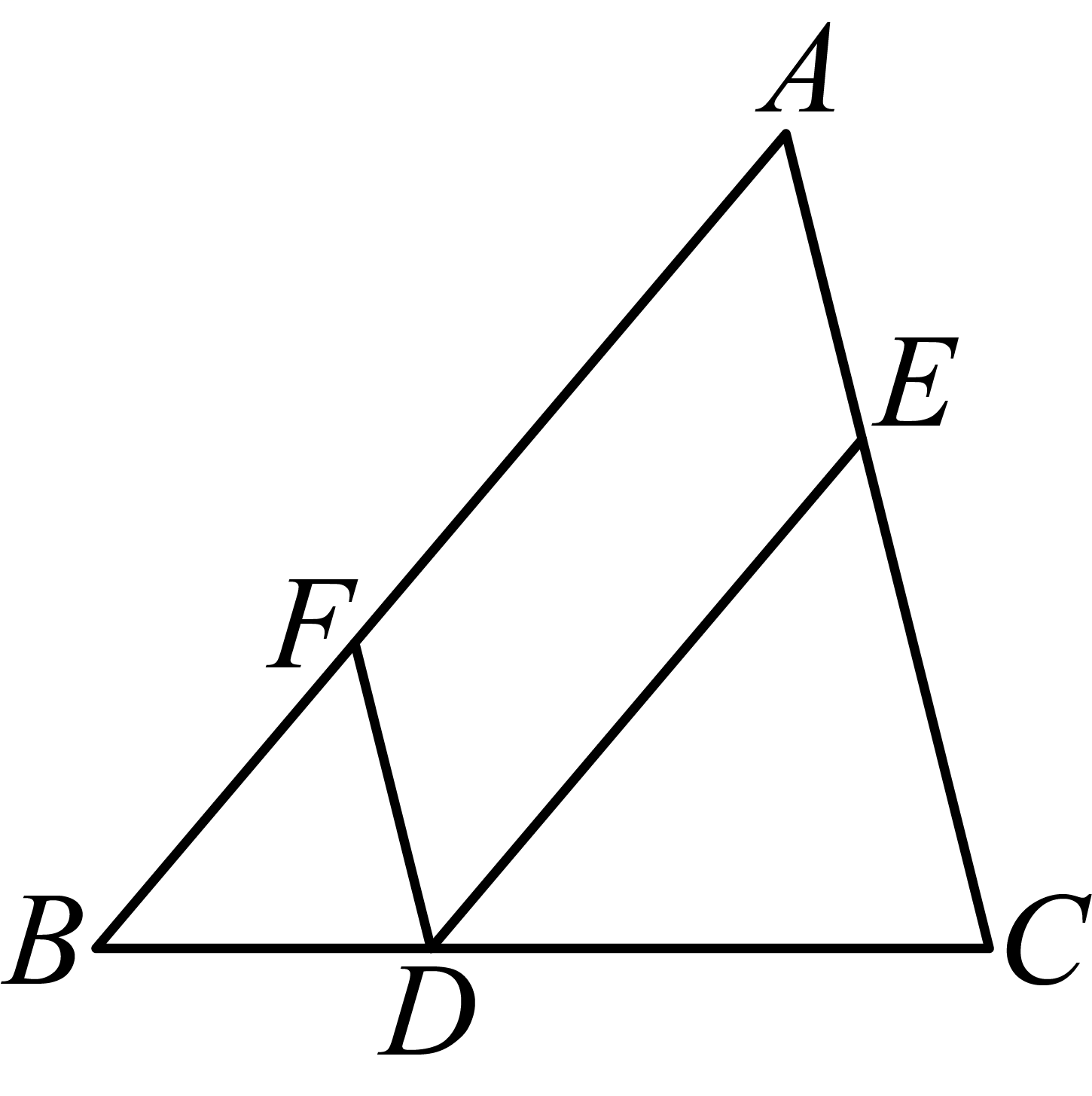$△ A B C$ 的边 $B C$ ， $A C$ ， $A B$ 上的点， $D F ∥ C A$ ， $∠ A = ∠ E D F$ ，

(1)、求证：四边形 $A F D E$ 为平行四边形；

(2)、若 $\frac{B D}{D C} = \frac{3}{5}$ ，直接写出 $\frac{S_{△ B D F}}{S_{△ C D E}}$ 的值为．

查看试题解析
20. 今年4月 $15$ 日是我国第八个“全民国家安全教育日”．为增强学生国家安全意识，夯实国家安全教育基础、某市举行国家安全知识竞赛．竞赛结束后，发现所有参赛学生的成绩（满分 $100$ 分）均不低于 $60$ 分．小明将自己所在班级学生的成绩（用x表示）分为四组：A组（ $60 \leq x < 70$ ），B组（ $70 \leq x < 80$ ），C组（ $80 \leq x < 90$ ），D组（ $90 \leq x \leq 100$ ），绘制了如图不完整的频数分布直方图和扇形统计图．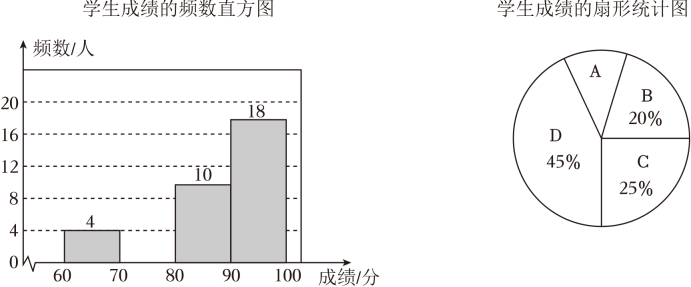
根据以上信息，解答下列问题：

(1)、补全频数分布直方图；

(2)、扇形统计图中A组所对应的圆心角的度数为 $°$ ；

(3)、把每组中各个同学的成绩用这组数据的中间值（如A组： $60 \leq x < 70$ 的中间值为 $65$ ）来代替，试估计小明班级的平均成绩；

(4)、小明根据本班成绩，估计全市参加竞赛的所有 $8000$ 名学生中会有 $800$ 名学生成绩低于 $70$ 分，实际只有 $446$ 名学生的成绩低于 $70$ 分．请你分析小明估计不准确的原因．

查看试题解析
21. 如图，两个相同的可以自由转动的转盘A和B ，转盘A被三等分，分别标有数字6，2，1；转盘B被四等分，分别标有数字 $- 1$ ， $- 2$ ， $- 3$ ， $- 6$ .（当指针指在两个扇形的交线时，需重新转动转盘）

(1)、转动转盘B一次，转盘停止时，指针指向偶数的概率为；

(2)、同时转动两个转盘，转盘停止时，求两个指针指向的数字之和大于0的概率.（画树状图或列表法）

查看试题解析
22. 某商家销售某种商品，每件进价为40元．经市场调查发现，该商品一周的销售量y（大于0的整数）件与销售单价x（不低于50的整数）满足一次函数关系，部分调查数据如表：
销售单价x（元/件）
50
55
60
70
75
…
一周的销售量y（件）
500
450
400
300
250
…

(1)、直接写出销售量y关于销售单价x的函数表达式：y＝．

(2)、若一周的销售利润为2750元，则销售单价是多少元/件？

(3)、现商家决定将商品一周的销售利润作为捐款寄往贫困地区，则捐款能达到的最大值是元．

查看试题解析
23.

(1)、【基础巩固】如图1，在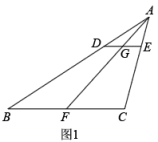 $△ A B C$ 中，D，E，F分别为 $A B$ ， $A C$ ， $B C$ 上的点， $D E ∥ B C$ ， $B F = C F$ ， $A F$ 交 $D E$ 于点G，求证： $D G = E G$ .

(2)、【尝试应用】如图2，在（1）的条件下，连接 $C D$ ， $C G$ .若 $C G ⊥ D E$ ， $C D = 10$ ， $A E = 6$ ，求 $\frac{D E}{B C}$ 的值.

(3)、【拓展提高】如图3，在 $▱ A B C D$ 中， $∠ A D C = 45 °$ ， $A C$ 与 $B D$ 交于点O，E为 $A O$ 上一点， $E G ∥ B D$ 交 $A D$ 于点G， $E F ⊥ E G$ 交 $B C$ 于点F.若 $∠ E G F = 40 °$ ， $F G$ 平分 $∠ E F C$ ， $F G = 8$ ，求 $B F$ 的长.

查看试题解析
24. 筒车是我国古代利用水力驱动的灌溉工具，如图，半径为3m的筒车⊙O按逆时针方向每分钟转 $\frac{5}{6}$ 圈，筒车与水面分别交于点A、B ，筒车的轴心O距离水面的高度OC为2.2m ，筒车上均匀分布着若干个盛水筒，若以某个盛水筒P刚浮出水面（点A）时开始计算时间．

(1)、求盛水筒P从A点到达最高点所经过的路程；

(2)、求浮出水面3.4秒时，盛水筒P到水面的距离；

(3)、若接水槽MN所在直线是⊙O的切线，且与直线AB交于点M ， MO＝8m ，直接写出盛水筒P从最高点开始，经过多长时间恰好第一次落在直线MN上．（参考数据：cos43°＝sin47°≈ $\frac{11}{15}$ ， sin16°＝cos74°≈ $\frac{11}{40}$ ， sin22°＝cos68°≈ $\frac{3}{8}$ ）

查看试题解析

25. 阅读与应用

我们知道 ${(a - b)}^{2} \geq 0$ ，即 $a^{2} - 2 a b + b^{2} \geq 0$ ，所以 $a^{2} + b^{2} \geq 2 a b$ （当且仅当 $a = b$ 时取等号）.

阅读1：若 $a ， b$ 为实数，

且 $a > 0 ， b > 0$ ，

$∵ {(\sqrt{a} - \sqrt{b})}^{2} \geq 0$

$∴ a - 2 \sqrt{a b} + b \geq 0$

$∴ a + b \geq 2 \sqrt{a b}$ （当且仅当 $a = b$ 时取等号）

阅读2：若函数 $y = x + \frac{m}{x}$ （ $x > 0 ， m > 0 ， m$ 为常数），

$∵ x > 0 ， m > 0$ ，

由阅读1的结论可知 $x + \frac{m}{x} \geq 2 \sqrt{x \cdot \frac{m}{x}}$ ，即 $x + \frac{m}{x} \geq 2 \sqrt{m}$

$∴$ 当 $x = \frac{m}{x}$ 时，函数 $y = x + \frac{m}{x}$ 有最小值，最小值为 $2 \sqrt{m}$ .

阅读理解以上材料，解答下列问题：

(1)、当

x =

时，函数

y = x + \frac{4}{x} (x > 0)

有最小值，最小值为.

(2)、疫情防控期间，某核酸检测采样点用隔离带分区管理，如图是一边靠墙其它三边用隔离带围成的面积为

32 m^{2}

的矩形隔离区域，假设墙足够长，则这个矩形隔离区域的长和宽分别是多少时，所用隔离带的长度最短？

(3)、随着高科技赋能传统快递行业，某大型物流公司为提高工作效率引进一批分拣机器人，已知每台机器人的运营成本包含以下三个部分：一是进价为25000元；二是材料损耗费，每小时为7元；三是折旧费，折旧费y（元）与运营工作时间t（小时）的函数关系式为

y = 0.1 t^{2} (t > 0)

.当运营工作时间t长达多少小时时，每台机器人平均每小时的运营成本最低？最低运营成本是多少？

查看试题解析

26. 如图， $A B$ 是 $⊙ O$ 的直径，点 $C, D$ 在 $⊙ O$ 上， $A D$ 平分 $∠ C A B$ ，过点 $D$ 作 $A C$ 的垂线交 $A C$ 的延长线于点 $E$ ，交 $A B$ 的延长线于点 $F$ ，连接 $B D$ ．

(1)、求证： $E F$ 是 $⊙ O$ 的切线；

(2)、求证： $A B \cdot (A B - A E) = A C \cdot B F$

(3)、若 $A B = 10, A C = 6$ ，求 $A D$ 的长．

查看试题解析
27. 定义：点P（m ， m）是平面直角坐标系内一点，将函数l的图象位于直线x＝m左侧部分，以直线y＝m为对称轴翻折，得到新的函数l^'的图象，我们称函数l^'的函数是函数l的相关函数，函数l^'的图象记作F₁ ，函数l的图象未翻折的部分记作F₂ ，图象F₁和F₂合起来记作图象F ．
例如：函数l的解析式为y＝x²﹣1，当m＝1时，它的相关函数l^'的解析式为y＝﹣x²+3（x＜1）．

(1)、如图，函数l的解析式为y＝﹣ $\frac{1}{2}$ x+2，当m＝﹣1时，它的相关函数l^'的解析式为y＝．

(2)、函数l的解析式为y＝﹣ $\frac{3}{x}$ ，当m＝0时，图象F上某点的纵坐标为﹣2，求该点的横坐标．

(3)、已知函数l的解析式为y＝x²﹣4x+3，
①已知点A、B的坐标分别为（0，2）、（6，2），图象F与线段AB只有一个公共点时，结合函数图象，求m的取值范围；
②若点C（x ， n）是图象F上任意一点，当m﹣2≤x≤5时，n的最小值始终保持不变，求m的取值范围（直接写出结果）．

查看试题解析

销售单价x（元/件）	50	55	60	70	75	…
一周的销售量y（件）	500	450	400	300	250	…