湖北省武汉市江汉区2023-2024学年八年级下学期期中数学试题

试卷更新日期：2024-05-08 类型：期中考试

进入出卷网下载

一、选择题（共10小题，每小题3分，共30分）

1. 要使二次根式 $\sqrt{x - 1}$ 有意义，则x的取值范围是（）

A、 $x ≥ 1$ B、 $x > 1$ C、 $x \leq 1$ D、 $x < 1$

查看试题解析
2. 下列二次根式是最简二次根式的是（）

A、 $\sqrt{0.5}$ B、 $\sqrt{6}$ C、 $\sqrt{8}$ D、 $\sqrt{\frac{1}{5}}$

查看试题解析
3. $▱ A B C D$ 中，已知 $∠ A + ∠ C = 100 °$ ，则 $∠ B$ 的大小为（）

A、 $50 °$ B、 $80 °$ C、 $100 °$ D、 $130 °$

查看试题解析
4. 下列计算中，正确的是（）

A、 $\sqrt{5} + \sqrt{2} = \sqrt{7}$ B、 $\sqrt{5} - \sqrt{2} = \sqrt{3}$ C、 $\sqrt{15} \div \sqrt{3} = \sqrt{5}$ D、 $2 \times \sqrt{5} = \sqrt{10}$

查看试题解析
5. 矩形具有而菱形不一定具有的性质是（）

A、对角相等 B、对角线相等 C、对角线互相平分 D、对角线互相垂直

查看试题解析
6. 已知a ， b ， c分别为 $△ A B C$ 的三条边，满足下列条件时， $△ A B C$ 不是直角三角形的是（）

A、 $∠ A + ∠ B = ∠ C$ B、 $a^{2} - b^{2} = c^{2}$ C、 $∠ A : ∠ B : ∠ C = 3 : 4 : 5$ D、 $a = 3, b = 4, c = \sqrt{7}$

查看试题解析
7. 下列命题中，逆命题是假命题的是（）

A、两直线平行，同位角相等 B、两个数互为相反数，则它们的平方相等 C、有一个内角是直角的四边形是矩形 D、线段的垂直平分线上的点到线段两端点的距离相等

查看试题解析
8. 小明沿正东方向走80m后，又沿另一方向走了60m，这时距出发地100m，则小明第二次行走的方向是（）

A、正南分向 B、正北方向 C、东南或东北方向 D、正南或正北方向

查看试题解析
9. 如图，一双长 $20 c m$ 的筷子置于底面直径为 $12 c m$ ，高为 $9 c m$ 的圆柱形热干面碗中，则筷子露在碗外面的长度不可能是（）

A、 $4 c m$ B、 $5 c m$ C、 $8 c m$ D、 $10 c m$

查看试题解析
10. 已知四边形 $A B C D$ ，以下有四组条件：① $A B ∥ C D, A B = C D$ ；② $A B = A D, C B = C D$ ；③ $∠ A = ∠ B, ∠ C = ∠ D$ ；④ $A B ∥ C D, A D = B C$ ，其中能判四边形 $A B C D$ 是平行四边形的条件共有（）

A、1组 B、2组 C、3组 D、1组

查看试题解析

二、填空题(共6小题，每小题3分，共18分

11. $\sqrt{{(- 4)}^{2}} =$ ．

查看试题解析
12. 比较大小： $2 \sqrt{6}$ $5$ ．（填“>”、“<”或“=”号）

查看试题解析
13. 已知一个直角三角形的两直角边长分别是 $3$ 和 $5$ ，则这个三角形的斜边长是．

查看试题解析
14. 若菱形的两条对角线长分别是 $6 c m$ 和 $8 c m$ ，则菱形一边上的高是 $c m$ ．

查看试题解析
15. 如图，在 $△ A B C$ 中，D ， E分别是 $A B ， A C$ 的中点， $F$ 是 $D E$ 上一点，且 $∠ A F C = 90 °$ ，若 $B C = 12 c m, A F = 6 c m, F C = 8 c m$ ，则 $D F$ 的长是 $c m$ ．

查看试题解析
16. 如图是用八个全等的直角三角形排成的“弦图”．记图中正方形 $A B C D$ ，正方形 $E F G H$ ，正方形 $M N K T$ 的面积分別为 $S_{1}, S_{2}, S_{3}$ ，若正方形 $E F G H$ 的边长为 $\sqrt{6}$ ，则 $S_{1} + S_{2} + S_{3} =$ ．

查看试题解析

三、解答题（共5小题，共52分）

17. 计算：

(1)、 $\sqrt{12} \times \sqrt{3} + \sqrt{8} - \sqrt{\frac{1}{2}}$ ；

(2)、 $(4 \sqrt{6} - 6 \sqrt{2}) \div 2 \sqrt{2}$ ．

查看试题解析
18. 如图，已知 $▱ A B C D$ ， E ， F是对角线 $B D$ 上的两点， $B E = D F$ ，连接 $A F, C E, A E, C F$ ．

(1)、求证： $A E = C F$ ；

(2)、连 $A C$ ，直接写出当 $A C$ 和 $B D$ 满足什么关系时，四边形 $A E C F$ 是菱形．

查看试题解析
19. 如图，四边形 $A B C D$ 中， $∠ B = 30 °$ ，过点A作 $A E ⊥ B C$ 于点E ， E恰好是 $B C$ 的中点，若 $A E = \sqrt{3}, D C = 1, A D = \sqrt{13}$ ．

(1)、直接写出四边形 $A B C D$ 的周长；

(2)、求四边形 $A B C D$ 的面积．

查看试题解析
20. 如图，在菱形ABCD中，对角线AC，BD交于点O，过点A作 $A E ⊥ B C$ 于点E，延长BC到点F，使CF=BE，连接DF．

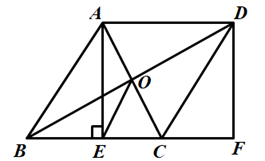(1)、求证：四边形AEFD是矩形；

(2)、连接OE，若AD=10，EC=4，求OE的长度．

查看试题解析
21. 如图是由边长为1的小正方形组成的 $9 \times 7$ 的网格，网格线的交点称为格点．中A ， B ， C ， M都是格点，O是 $A B$ 与网格线的交点，仅用无刻度的直尺在给定的网格中完成下列画图．

(1)、画出平行四边形 $A B C D$ ；

(2)、在 $A B$ 左侧画出所有满足条件的格点P ，使 $O P = O A$ ；

(3)、在 $A B$ 上画一点N ，使 $A N = A M$ ；

(4)、连接 $A C$ ，在 $A C$ 上画点Q ，使 $∠ B Q C = ∠ A Q O$ ．

查看试题解析

四、填空题(共4小题，每小题4分，共16分

22. 已知 $m = \sqrt{5} + 2$ ， $n = \sqrt{5} - 2$ ，则 $m^{2} - m n + n^{2}$ 的值为.

查看试题解析
23. 最简二次根式 $\sqrt{2 a^{2} + a - 1}$ 和最简二次根式 $2 \sqrt{a^{2} + a + 8}$ 的和为最简二次根式 $m \sqrt{n}$ ，则 $m =$ ， $n =$ ．

查看试题解析
24. 如图， $▱ A B C D$ 中， $A C = 2 A B$ ，对角线 $A C$ 、 $B D$ 交于点O ， M ， N分别是 $O A$ 、 $O D$ 的中点，过点 $O$ 作 $E F ∥ A B$ ，分别交 $A D$ ， $B C$ 于点E ， F ，连 $A F$ ， $M F$ ．下列四个结论：① $E O = \frac{1}{2} C D$ ；② $A F = E F$ ；③ $S_{△ M O N} = S_{△ M O F}$ ；④ $F M ⊥ B D$ ．
其中正确的结论是(填写序号)．

查看试题解析
25. 已知，如图，矩形 $A B C D$ 中， $A B = 4$ ， $A D = 3$ ， E是射线 $B C$ 上一动点，将矩形 $A B C D$ 沿直线 $A E$ 翻折．点B落在点F处，若 $△ C E F$ 为直角三角形，则 $C F$ 的值是．

查看试题解析

五、解答题(共3小题，共34分

26. 如图，已知菱形 $A B C D$ ， $E$ 为 $C B$ 延长线上一点．且 $B E = B C$ ．

(1)、求证： $A E ⊥ A C$ ；

(2)、如图（2），点 $P$ 为线段 $A E$ 上一点，连接 $P D$ ， $M$ 为 $P D$ 的中点，连接 $B P$ ， $A M$ ．求证： $B P = 2 A M$ ；

(3)、在（2）的条件下，若 $∠ A B C = 60 °$ ， $B P ⊥ A P$ ，菱形 $A B C D$ 的面积为 $12 \sqrt{3}$ ，直接写出 $△ A P D$ 的面积．

查看试题解析
27. 阅读材料：对于平面直角坐标系中的任意两点 $M_{1} (x_{1}, y_{1}), M_{2} (x_{2}, y_{2})$ ．我们把 $d = \sqrt{{(x_{1} - x_{2})}^{2} + {(y_{1} - y_{2})}^{2}}$ 叫做 $M_{1}, M_{2}$ 两点间的距离，记作 $d (M_{1}, M_{2})$ ．如 $A (- 2, 3), B (2, 5)$ ，则 $d (A, B) = \sqrt{{(- 2 - 2)}^{2} + {(3 - 5)}^{2}} = 2 \sqrt{5}$ ．
请根据以上阅读材料，解答下列问题：

(1)、①若 $A (3 \sqrt{2}, 0), B (0, 4 \sqrt{2})$ ，直接写山 $d (A, B)$ 的值；
②当 $A (a, 1), B (- 1, 4)$ 距离 $d (A, B) = 5$ 时，求出 $a$ 的值；

(2)、①若在平面内有一点 $C (x, y)$ ，使式子 $\sqrt{{(x + 3)}^{2} + {(y - 4)}^{2}} + \sqrt{{(x - 2)}^{2} + {(y - 4)}^{2}}$ 有最小值，直接写出这个最小值；
②直接写出 $\sqrt{{(m - 3)}^{2} + 1} + \sqrt{m^{2} + n^{2}} + \sqrt{4 + {(n - 6)}^{2}}$ 的最小值．

查看试题解析
28. 如图（1），在平面直角坐标系中， $A (a, b)$ ，且 $\sqrt{a^{2} + b^{2} - 2 a b} + | a - \sqrt{2} | = 0$ ， $A B ⊥ y$ 轴于点B ， $C$ 为 $x$ 轴负半轴上一点，且 $O C = O B$ ．

(1)、求A ， B ， C三个点的坐标并直接判断四边形 $A B C O$ 的形状；

(2)、如图（2），E ， F分别为 $B C ， A O$ 上的点， $O D ⊥ B F$ 于点 $D$ ．连 $A D$ 并延长交 $O E$ 的延长线于点 $M$ ．若 $C E = A F, ∠ M = 1 5^{°}$ ．求 $M E + D F$ 的值；

(3)、如图（3），若 $H$ 为 $△ A B O$ 的角平分线的交点， $P H ⊥ O H, P H$ 分别交 $A B ， B C$ 于点 $P^{^{'}}, Q$ ，求 $B C ， B P$ 之间的数量关系．

查看试题解析