湖北省荆门市京山市2023-2024学年八年级下学期期中数学试题
试卷更新日期:2024-05-08 类型:期中考试
一、选择题(本题共10小题,每小题3分,共30分)
-
1. 若在实数范围内有意义,则a的取值范围是( )A、 B、 C、 D、2. 下列各组中的三条线段,能组成直角三角形的是( )A、3,3,5 B、4,5,6 C、6,8,10 D、3. 若平行四边形中两个内角的度数比为1:2,则其中较小的内角是( )A、60° B、90° C、120° D、45°4. 化简的结果是( )A、5 B、-5 C、±5 D、255. 矩形ABCD中,AB=3,两条对角线AC、BD所夹的钝角为120°,则对角线BD的长为( )
 A、6 B、3 C、 D、6. 下列二次根式中,是最简二次根式的是( )A、 B、 C、 D、7. 如图,在△ABC中,AB=3,AC=5,AD平分∠BAC , AD⊥BF于点D , 点E为BC的中点,连接DE , 则DE的长是( )
A、6 B、3 C、 D、6. 下列二次根式中,是最简二次根式的是( )A、 B、 C、 D、7. 如图,在△ABC中,AB=3,AC=5,AD平分∠BAC , AD⊥BF于点D , 点E为BC的中点,连接DE , 则DE的长是( ) A、0.5 B、0.75 C、1 D、28. “赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a,较短直角边长为b.若ab=8,大正方形的面积为25,则小正方形的边长为( )
A、0.5 B、0.75 C、1 D、28. “赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a,较短直角边长为b.若ab=8,大正方形的面积为25,则小正方形的边长为( ) A、9 B、6 C、4 D、39. 四边形ABCD中,对角线AC、BD相交于点O,给出下列四个条件:①AD∥BC;②AD=BC;③OA=OC;④OB=OD,从中任选两个条件,能使四边形ABCD为平行四边形的选法有( ).A、3种 B、4种 C、5种 D、6种10. 如图,将矩形沿折叠后点与重合.若原矩形的长宽之比为 , 则的值为( )
A、9 B、6 C、4 D、39. 四边形ABCD中,对角线AC、BD相交于点O,给出下列四个条件:①AD∥BC;②AD=BC;③OA=OC;④OB=OD,从中任选两个条件,能使四边形ABCD为平行四边形的选法有( ).A、3种 B、4种 C、5种 D、6种10. 如图,将矩形沿折叠后点与重合.若原矩形的长宽之比为 , 则的值为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本题共5小题,每小题3分,共15分)
-
11. 写出一个比3小的正无理数 .12. 如图,在菱形ABCD中,∠BAD=60°,BD=4,则菱形ABCD的周长是.
 13. 如图,从一个大正方形裁去面积为15cm2和24cm2的两个小正方形,则留下的部分的面积为cm2.
13. 如图,从一个大正方形裁去面积为15cm2和24cm2的两个小正方形,则留下的部分的面积为cm2. 14. 如图,所有阴影部分四边形都是正方形,所有三角形都是直角三角形,若正方形A、C、D的面积依次为4、6、18,则正方形B的面积为
14. 如图,所有阴影部分四边形都是正方形,所有三角形都是直角三角形,若正方形A、C、D的面积依次为4、6、18,则正方形B的面积为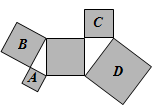 15. 如图,在中,是的中点,作 , 垂足在线段上,连接、 , 则下列结论中:①;②;③;④ . 一定成立的是 . (只填序号).
15. 如图,在中,是的中点,作 , 垂足在线段上,连接、 , 则下列结论中:①;②;③;④ . 一定成立的是 . (只填序号).
三、解答题(本题共8小题,共72分)
-
16. 计算(1)、(2)、17. 如图,小明为了测得学校旗杆的高度,他先将旗绳拉直,绳尾端正好落在地面点,此时,点到杆底点距离 , 他又将旗绳拉直到杆底部点,此时,绳子多出一截 , 量得多出部分长度为 , 请你帮他计算出旗杆的高度.
 18. 如图,在中,点、分别是、的中点. 求证:四边形是平行四边形.
18. 如图,在中,点、分别是、的中点. 求证:四边形是平行四边形. 19. 如图,菱形花坛的边长为 , , 沿着菱形的对角线修建两条小路和 .
19. 如图,菱形花坛的边长为 , , 沿着菱形的对角线修建两条小路和 . (1)、求和的长;(2)、求菱形花坛的面积.20. 如图,每个小正方形的边长都为1
(1)、求和的长;(2)、求菱形花坛的面积.20. 如图,每个小正方形的边长都为1 (1)、求四边形的面积与周长;(2)、是直角吗?21. 已知正六边形 , 请用无刻度直尺画图,画图过程用虚线表示,画图结果用实线表示.
(1)、求四边形的面积与周长;(2)、是直角吗?21. 已知正六边形 , 请用无刻度直尺画图,画图过程用虚线表示,画图结果用实线表示. (1)、在图1中,画出一个以BD为边的等边三角形;(2)、在图2中,画出一个以CD为边的矩形;(3)、在图3中,画出一个以BC为边的菱形;(4)、在图4中,画出一个以AB为边的平行四边形(非矩形、非菱形).22. 阅读材料:
(1)、在图1中,画出一个以BD为边的等边三角形;(2)、在图2中,画出一个以CD为边的矩形;(3)、在图3中,画出一个以BC为边的菱形;(4)、在图4中,画出一个以AB为边的平行四边形(非矩形、非菱形).22. 阅读材料:我国南宋数学家秦九韶(约1202—1261)在《数书九章》中记述了“三斜求积术”,即已知三角形的三边长,求它的面积,用现代式子表示即为:S= . ①(其中为三角形的面积,a、b、c为三角形的三边长).而古希腊的几何学家海伦(Heron , 约公元50年),在《度量》中也有求三角形面积的“海伦公式”:②(其中S为三角形的面积,a、b、c为三角形的三边长,为半周长,即).
我国宋代数学家秦九韶提出的“三斜求积术”与这个公式基本一致,所以这个公式也叫“海伦—秦九韶公式”.
解答问题:
(1)、若在中,已知 , 试分别运用公式①和公式②计算的面积;(2)、请你写出由公式①推导出公式②的过程;(3)、计算(1)中的BC边上的高.

