湖北省咸宁市嘉鱼县2023-2024学年八年级下学期期中数学试题

试卷更新日期：2024-05-08 类型：期中考试

进入出卷网下载

一、精心选一选（本大题共10小题，每小题3分，满分30分．每小题给出的4个选项中只有一个符合题意，请在答题卷上把正确答案的代号涂黑）

1. 若代数式 $\sqrt{x - 1}$ 有意义，则 $x$ 的取值范围是（）

A、 $x \geq - 1$ B、 $x \neq 1$ C、 $x \geq 1$ D、 $x \leq 1$

查看试题解析
2. 下列根式中是最简二次根式的是（）

A、 $\sqrt{4}$ B、 $\sqrt{6}$ C、 $\sqrt{20}$ D、 $\sqrt{0.5}$

查看试题解析
3. 下列计算错误的是（）

A、3+2 $\sqrt{2}$ =5 $\sqrt{2}$ B、 $\sqrt{8}$ ÷2= $\sqrt{2}$ C、 $\sqrt{2}$ × $\sqrt{3}$ = $\sqrt{6}$ D、 $\sqrt{8}$ $- \sqrt{2}$ = $\sqrt{2}$

查看试题解析
4. 在 $△ A B C$ 中， $A B = 1$ ， $A C = \sqrt{3}$ ， $B C = 2$ ，则这个三角形是（）

A、等腰直角三角形 B、直角三角形 C、钝角三角形 D、等腰三角形

查看试题解析
5. 四边形ABCD中，对角线AC、BD相交于点O，下列条件不能判定这个四边形是平行四边形的是（）

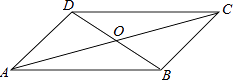A、AB∥DC，AD∥BC B、AB=DC，AD=BC C、AO=CO，BO=DO D、AB∥DC，AD=BC

查看试题解析
6. 对角线长为2的正方形的面积是（）

A、2 B、4 C、 $\sqrt{2}$ D、 $4 \sqrt{2}$

查看试题解析
7. 如图，矩形ABCD的对角线AC=8cm，∠AOD=120°，则AB的长为（）

A、 $\sqrt{3}$ cm B、2cm C、2 $\sqrt{3}$ cm D、4cm

查看试题解析
8. 如图，已知 $P$ 是菱形 $A B C D$ 的边 $B C$ 上一点，且 $∠ D A P = ∠ B = 70 °$ ，那么 $∠ C D P$ 的度数为（）

A、15° B、25° C、30° D、35°

查看试题解析
9. 甲乙两艘客轮同时离开港口 $A$ ，航行的速度都是 $40 m / m i n$ ，甲客轮用时 $15 m i n$ 到达港口 $B$ ，乙客轮用时 $20 m i n$ 到达港口 $C$ ，且港口 $B$ 和港口 $C$ 的直线距离是 $1000 m$ ，若甲客轮沿着北偏东30°的方向航行，则乙客轮的航行方向可能是（）

A、北偏西30° B、南偏西30° C、南偏西60° D、南偏东60°

查看试题解析
10. 如图，在 $△ A B C$ 中，点 $D$ 是 $A C$ 的中点，点 $P$ 在 $△ A B C$ 的内部， $∠ 1 = ∠ 2$ ， $∠ A P B = 90 °$ ，若 $A B = 4$ ， $B C = 6$ ，则 $P D$ 的长为（）

A、1 B、 $\sqrt{2}$ C、1.5 D、2

查看试题解析

二、细心填一填（本大题共6小题，每小题3分，满分18分．请把答案填在答题卷相应题号的横线上）

11. 化简： $\sqrt{72}$ = ．

查看试题解析
12. 若 $\sqrt{60 m}$ 是正整数，则整数 $m$ 可取的最小值为．

查看试题解析
13. 在 $△ A B C$ 中， $∠ A$ 、 $∠ B$ 、 $∠ C$ 的对边分别为 $a$ 、 $b$ 、 $c$ ，且 $b^{2} - a^{2} = c^{2}$ ，若 $∠ A = 70 °$ ，则 $∠ C$ 的大小是．

查看试题解析
14. 如图，平行四边形 $A B C D$ 中， $A D = 3$ ， $A B = 5$ ， $∠ A D B = 90 °$ ，则平行四边形 $A B C D$ 的面积为．

查看试题解析
15. 已知 $a = \sqrt{5} - 3$ ，则代数式 $a^{2} + 6 a + 7$ 的值是．

查看试题解析
16. 如图，点 $E$ 在菱形 $A B C D$ 的边 $B C$ 上， $A E = F E$ ， $∠ A E F = ∠ B = 100 °$ ，则 $∠ D C F$ 的大小为．

查看试题解析

三、专心解一解（本大题共8小题，满分72分．请认真读题，冷静思考，解答题应写出文字说明，证明过程或演算步骤）

17. 计算：

(1)、 $\sqrt{12} - 6 \sqrt{\frac{1}{3}} + \sqrt{48}$ ；

(2)、 $a^{2} \sqrt{8 a} + 3 a \sqrt{50 a^{3}}$ ．

查看试题解析
18. 如图，四边形 $A B C D$ 是矩形，对角线 $A C$ 、 $B D$ 相交于点 $O$ ， $B E ∥ A C$ 交 $D C$ 的延长线于点 $E$ ．求证： $B D = B E$ ．

查看试题解析
19. 已知： $a = \sqrt{5} + 2$ ， $b = \sqrt{5} - 2$ ，分别求下列代数式的值：

(1)、 $a^{2} - b^{2}$ ；

(2)、 $a^{2} + 3 a b + b^{2}$ ．

查看试题解析
20. 阅读下列内容，并解决问题．
一道习题引发的思考
小明在学习《勾股定理》一章内容时，遇到了一个习题，并对有关内容进行了研究：
【问题呈现】古希腊的哲学家柏拉图曾指出，如果 $m$ 表示大于1的整数， $a = 2 m$ ， $b = m^{2} - 1$ ， $c = m^{2} + 1$ ，那么 $a$ ， $b$ ， $c$ 为勾股数．你认为对吗？如果对，你能利用这个结论得出一些勾股数吗？
【资料搜集】定义：勾股数是指可以构成一个直角三角形三边的一组正整数．一般地，若三角形三边长 $a$ ， $b$ ， $c$ 都是正整数，且满足 $a^{2} + b^{2} = c^{2}$ ，那么 $a$ ， $b$ ， $c$ 称为一组勾股数．
关于勾股数的研究；我国西周初数学家商高在公元前1000年发现了“勾三，股四，弦五”，这组数（3、4、5）是世界上最早发现的一组勾股数．毕达哥拉斯学派、柏拉图学派、我国数学家刘徽、古希腊数学家丢番图都进行过勾股数的研究，习题中的表达式是柏拉图给出的勾股数公式，这个表达式未给出全部勾股数．世界上第一次给出勾股数通解公式的是《九章算术》．
【问题解决】

(1)、根据柏拉图的研究，当 $m = 6$ 时，请直接写出一组勾股数：；

(2)、若 $m$ 表示大于1的整数，试证明 $(m^{2} - 1, 2 m, m^{2} + 1)$ 是一组勾股数；

(3)、请举出一个反例（即写出一组勾股数），说明柏拉图给出的勾股数公式不能构造出所有的勾股数．

查看试题解析
21. 如图，在四边形 $A B C D$ 中， $∠ B = 90 °$ ， $A B = B C = 2$ ， $A D = \sqrt{2}$ ， $C D = \sqrt{10}$ ．

(1)、求 $∠ D A B$ 的度数．

(2)、连接BD ，求BD的长．

查看试题解析
22. 如图，在平面直角坐标系中，已知 $A (0, 2)$ ， $B (0, - 3)$ ， $C (4, 0)$ ， $P (- 2, 0)$ ，且以 $A$ ， $B$ ， $C$ ， $D$ 为顶点的四边形为菱形．

(1)、直接写出 $D$ 点的坐标；

(2)、请用无刻度直尺作直线，使直线经过点 $P$ 且平分菱形的面积，保留作图痕迹；

(3)、已知点 $T$ 是CD边上一点，若线段OT将菱形ABCD的面积分为2：3两部分，直接写出点 $T$ 的坐标．

查看试题解析
23.

(1)、【问题提出】如图1，在四边形ABCD中， $∠ B A D = 60 °$ ， $∠ B C D = 120 °$ ， $A B = A D$ ，连接AC ．试探究BC、CD、AC之间的数量关系．
小明的思路是：他发现 $∠ B A D$ 和 $∠ B C D$ 互补，推得 $∠ B + ∠ A D C = 180 °$ ，于是想到延长CD到点 $E$ ，使 $D E = B C$ ，连接AE ．从而得到 $∠ B = ∠ A D E$ ，然后证明 $△ A D E$ $≌ △ A B C$ ，不难得到BC、CD、AC之间的数量关系是；

(2)、【问题变式】如图2，四边形ABCD中， $∠ B A D = ∠ B C D = 90 °$ ， $A B = A D$ ，连接AC ，试探究BC、CD、AC之间的数量关系，并说明理由；

(3)、【问题拓展】如图3，四边形ABCD中， $∠ B A D = 120 °$ ， $∠ B C D = 60 °$ ， $A B = A D$ ，连接AC ，若 $A C = 2 \sqrt{3}$ ，求四边形ABCD的面积．（直接写出结果）

查看试题解析
24. 如图，在 $R t △ A B C$ 中， $∠ B A C = 90 °$ ， $∠ A C B = 30 °$ ， $A B = 6$ ，点 $P$ 为 $B C$ 上一个动点，连接PA ，以PA ， PC为邻边作平行四边形APCQ ，连接PQ交AC于点 $O$ ．

(1)、若 $A C = P Q$ ，求PB的长；

(2)、当PB长为何值时，平行四边形APCQ是菱形？为什么？

(3)、在点P的运动过程中，线段PQ的长度是否存在最小值，若存在，请直接写出最小值；若不存在，请说明理由．

查看试题解析