广东省茂名市高州市2024年中考一模数学试题

试卷更新日期：2024-05-08 类型：中考模拟

进入出卷网下载

一、选择题：本大题共10小题，每小题3分，共30分．在每个小题给出的四个选项中，只有一项是符合题目要求的．

1. 3的倒数是（）

A、 $3$ B、 $- 3$ C、 $\frac{1}{3}$ D、 $- \frac{1}{3}$

查看试题解析
2. 在下列四个几何体中，主视图与俯视图都是圆的为（）

A、 B、 C、 D、

查看试题解析
3. 一分钟仰卧起坐是监测学校体育与健康教育质量的一个项目．某校随机抽取了八年级10名女生的一分钟仰卧起坐测试数据进行统计，分别是40，38，32，34，40，38，45，50，40，45，那么这组数据的众数与中位数分别是（）

A、40，38 B、40，39 C、38，40 D、40，40

查看试题解析
4. 下列运算正确的是（）

A、 $x^{4} \cdot x^{3} = x^{12}$ B、 ${(a^{6})}^{2} \div {(a^{4})}^{3} = a$ C、 ${(a^{3})}^{2} \cdot a^{4} = a^{10}$ D、 ${(a b^{2})}^{3} \div {(- a b)}^{2} = - a b^{4}$

查看试题解析
5. 如图，点 $E$ 在 $A C$ 的延长线上，下列条件中能判断 $A B ∥ C D$ 的是（）

A、 $∠ D = ∠ D C E$ B、 $∠ 3 = ∠ 4$ C、 $∠ 1 = ∠ 2$ D、 $∠ A + ∠ A B D = 180 °$

查看试题解析
6. 把一副普通扑克牌中的13张红桃牌洗匀后正面向下放在桌子上，从中随机抽取一张，则抽到牌面数字是3的概率为（）

A、 $\frac{1}{13}$ B、 $\frac{1}{5}$ C、 $\frac{3}{13}$ D、 $\frac{3}{5}$

查看试题解析
7. 已知a是一元二次方程 $x^{2} - 2 x - 4 = 0$ 的一个根，则代数式 $a^{2} - 2 a$ 的值为（）

A、4 B、8 C、 $2 + 2 \sqrt{5}$ D、 $2 - 2 \sqrt{5}$

查看试题解析
8. 已知点 $P (x - 1, - 3)$ 在第四象限，则x的取值范围在数轴上可以表示为（）

A、 B、 C、 D、

查看试题解析
9. 如图， $A B$ 为 $⊙ O$ 的直径，点 $C ， D$ 为圆上两点，且 $C D = C B$ ，若 $∠ D A B = 50 °$ ，则 $∠ A B C =$ （）

A、 $60 °$ B、 $65 °$ C、 $50 °$ D、 $55 °$

查看试题解析
10. 如图所示，小亮设计了一个探究杠杆平衡条件的实验：在一根匀质的木杆中点O左侧固定位置B处悬挂重物A ，右侧用一个弹簧测力计向下拉，改变弹簧测力计与支点O的距离 $x (c m),$ ，观察弹簧测力计的示数 $y (N)$ 的变化情况．实验数据记录如下表：
$x (c m),$
……
10
15
20
25
30
……
$y (N)$
……
45
30
22.5
18
15
……
下列说法不正确的是（）

A、弹簧测力计的示数 $y (N)$ 与支点O的距离 $x (c m),$ 之间关系的图象如图 B、y与x的函数关系式为 $y = \frac{450}{x} (x > 0)$ C、当弹簧测力计的示数为 $12.5 N$ 时，弹簧测力计与O点的距离是37.5 D、随着弹簧测力计与O点的距离不断增大，弹簧测力计上的示数不断减小

查看试题解析

二、填空题：本大题共5小题，每小题3分，共15分．

11. 据报道，2023年“十一”假期，襄阳A级旅游景区共接待游客151100人次，数字151100用科学记数法表示是．

查看试题解析
12. 计算： $\sqrt{2} \times \sqrt{8}$ = .

查看试题解析
13. 在平面直角坐标系xOy中，若点 $(1 ， y_{1})$ ， $(4 ， y_{2})$ 在反比例函数 $y = \frac{k}{x} (k < 0)$ 的图像上，则 $y_{1}$ $y_{2}$ （填“ $>$ ”“ $=$ ”或“ $<$ ”）．

查看试题解析
14. 某公司今年一月盈利30万元，三月盈利36.3万元，从一月到三月，每月盈利的增长率都相同，设月平均增长率为x ，根据题意可列方程为．

查看试题解析
15. 如图，等边 $△ A B C$ 内接于 $⊙ O$ ， $A B = 4 \sqrt{3}$ ，则图中阴影部分的面积等于．

查看试题解析

三、解答题（一）：本大题共3小题，16、17小题各6分，18小题7分，共19分．

16. 解不等式组： ${\begin{array}{l} 6 - 2 x \geq 0 \\ \frac{x - 1}{2} - 1 < \frac{2 x - 4}{3} \end{array}$

查看试题解析
17. 先化简，再求值： $\frac{x^{2} - 4}{x^{2} + 4 x + 4} \div \frac{x^{2} - 2 x}{x + 2}$ ，其中 $x = \sqrt{2}$ ．

查看试题解析
18. 从地面竖直向上抛一个物体，物体向上的速度 $v (m / s)$ 是运动时间 $t (s)$ 的函数．经测量，速度 $v (m / s)$ 与时间 $t (s)$ 的关系如表：
时间 $t (s)$
1
1.5
2
速度 $v (m / s)$
20
15
10

(1)、写出速度 $v (m / s)$ 与时间 $t (s)$ 的关系式；

(2)、求经过多长时间，物体将达到最高点？

查看试题解析

四、解答题（二）：本大题共4小题，每小题8分，共32分．

19. 如图，点 $A$ ， $C$ ， $B$ ， $D$ 在 $8 \times 9$ 网格的格点上，每小方格是边长为1个单位长度的正方形．请按要求画图，并回答问题：

(1)、过点 $C$ 画直线 $A B$ 的垂线，垂足为 $E$ ；并直接写出点 $C$ 到直线 $A B$ 的距离；

(2)、过点 $A$ 画 $A F ∥ B C$ 交 $C E$ 于点 $F$ ；

(3)、请写出图中 $∠ C B D$ 的所有同位角．

查看试题解析
20. 某校加强了1分钟定时跳绳的训练后，抽样调查部分学生的“1分钟跳绳”成绩，并绘制了不完整的频数分布直方图和扇形图（如图）．根据图中提供的信息解决下列问题：
A： $80 \leq x < 100$
B： $100 \leq x < 120$
C： $120 ≤ x < 140$
D： $140 ≤ x < 160$
E： $160 ≤ x < 180$

(1)、抽样的人数是人，扇形中 $m =$ ；

(2)、抽样中D组人数是 ▲ 人，本次抽取的部分学生“1分钟跳绳”成绩组成的一组数据的中位数落在 ▲ 组（填 $A 、 B 、 C 、 D 、 E$ ），并补全频数分布直方图；

(3)、如果“1分钟跳绳”成绩大于等于160次为满分，那么该校2100名学生中“1分钟跳绳”成绩为满分的大约有多少人？

查看试题解析

21. 某校数学活动小组要测量校园内一棵古树的高度，王朵同学带领小组成员进行此项实践活动，记录如下：

填写人：王朵综合实践活动报告时间：2023年4月20日

活动任务：测量古树高度

活动过程

【步骤一】设计测量方案

小组成员讨论后，画出如图①的测量草图，确定需测的几何量．

【步骤二】准备测量工具

自制测角仪，把一根细线固定在半圆形量角器的圆心处，细线的另一端系一个小重物，制成一个简单的测角仪，利用它可以测量仰角或俯角，如图②所示准备皮尺．

【步骤三】实地测量并记录数据如图③，王朵同学站在离古树一定距离的地方，将这个仪器用手托起，拿到眼前，使视线沿着仪器的直径刚好到达古树的最高点．

如图④，利用测角仪，测量后计算得出仰角 $α$ ．

测出眼睛到地面的距离 $A B$ ．

测出所站地方到古树底部的距离 $B D$ ．

$α =$ ．

$A B = 1.54 m$ ．

$B D = 10 m$ ．

【步骤四】计算古树高度 $C D$ ．（结果精确到 $0.1 m$ ）

（参考数据： $s i n 40 ° = 0.643 ， c o s 40 ° = 0.766 ， t a n 40 ° = 0.839$ ）

请结合图①、图④和相关数据写出 $α$ 的度数并完成【步骤四】．

查看试题解析

22. 图①是古代的一种远程投石机，其投出去的石块运动轨迹是抛物线的一部分．据《范蠡兵法》记载：“飞石重十二斤，为机发，行二百步”，其原理蕴含了物理中的“杠杆原理”．在如图②所示的平面直角坐标系中，将投石机置于斜坡 $O A$ 的底部点O处，石块从投石机竖直方向上的点C处被投出，已知石块运动轨迹所在抛物线的顶点坐标是 $(50, 25)$ ， $O C = 5$ ．

(1)、求抛物线的表达式；

(2)、在斜坡上的点A建有垂直于水平线 $O D$ 的城墙 $A B$ ，且 $O D = 75$ ， $A D = 12$ ， $A B = 9$ ，点D ， A ， B在一条直线上．通过计算说明石块能否飞越城墙 $A B$ ．

查看试题解析

五、解答题（三）：本大题共2小题，每小题12分，共24分．

23. 如图，在 $△ A B C$ 中， $A B = 6, B C = 8, A C = 10$ ，以 $A B$ 为直径作 $⊙ O$ ，交 $A C$ 于点 $F$ ，连接 $C O$ 并延长，分别交 $⊙ O$ 于 $D 、 E$ 两点，连接 $B E, B D$ ．

(1)、求证： $B C$ 是 $⊙ O$ 的切线；

(2)、求证： $B C^{2} = C D \cdot C E$ ；

(3)、求 $∠ A B E$ 的正切值．

查看试题解析
24.

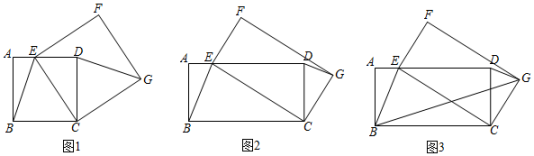(1)、【问题情境】如图1，四边形ABCD是正方形，点E是AD边上的一个动点，以CE为边在CE的右侧作正方形CEFG，连接DG、BE，则DG与BE的数量关系是；

(2)、【类比探究】
如图2，四边形ABCD是矩形，AB=2，BC=4，点E是AD边上的一个动点，以CE为边在CE的右侧作矩形CEFG，且CG：CE=1：2，连接DG、BE．判断线段DG与BE有怎样的数量关系和位置关系，并说明理由；

(3)、【拓展提升】
如图3，在（2）的条件下，连接BG，则2BG+BE的最小值为．

查看试题解析

$x (c m),$	……	10	15	20	25	30	……
$y (N)$	……	45	30	22.5	18	15	……

时间 $t (s)$	1	1.5	2
速度 $v (m / s)$	20	15	10