备考2024年中考数学重难创新题2 二次函数性质综合题
试卷更新日期:2024-05-07 类型:二轮复习
一、选择题
-
1. 定义:我们将顶点的横坐标和纵坐标互为相反数的二次函数称为“互异二次函数”.如图,在正方形 中,点 ,点 ,则互异二次函数 与正方形 有交点时 的最大值和最小值分别是( )
 A、4,-1 B、 ,-1 C、4,0 D、 ,-12. 已知 , 均为关于x的函数,当 时,函数值分别为 , ,若对于实数a,当 时,都有 ,则称 , 为亲函数,则以下函数 和 是亲函数的是( )A、 , B、 , C、 , D、 ,3. 在平面直角坐标系中,如果点P的横坐标和纵坐标相等,则称点P为和谐点.例如点(1,1),(﹣ , ﹣),(﹣ , ﹣),…,都是和谐点.若二次函数y=ax2+4x+c(a≠0)的图象上有且只有一个和谐点( , ),当0≤x≤m时,函数y=ax2+4x+c﹣(a≠0)的最小值为﹣3,最大值为1,m的取值范围是( )A、m≤4 B、m≥2 C、2≤m≤4 D、2<m<44. 定义: ,若函数 ,则该函数的最大值为( )A、0 B、2 C、3 D、45. 新定义:在平面直角坐标系中,对于点和点 , 若满足时,;时, , 则称点是点的限变点.例如:点的限变点是 , 点的限变点是 . 若点在二次函数的图象上,则当时,其限变点的纵坐标的取值范围是( )A、 B、 C、 D、6. 定义:若点P(a,b)在函数y= 的图象上,将以a为二次项系数,b为一次项系数构造的二次函数y=ax2+bx称为函数y=的一个“派生函数”.例如:点(2, )在函数y= 的图象上,则函数y=2x2+x称为函数y= 的一个“派生函数”.现给出以下两个命题:(1)存在函数y= 的一个“派生函数”,其图象的对称轴在y轴的右侧;(2)函数y= 的所有“派生函数”的图象都经过同一点.下列判断正确的是( )A、命题(1)与命题(2)都是真命题 B、命题(1)与命题(2)都是假命题 C、命题(1)是假命题,命题(2)是真命题 D、命题(1)是真命题,命题(2)是假命题7. 抛物线与轴的一个交点为 , 与轴交于点 , 点是抛物线的顶点,对称轴为直线 , 其部分图象如图所示,则以下个结论:; , 是抛物线上的两个点,若 , 且 , 则;在轴上有一动点 , 当的值最小时,则点的坐标为;若关于的方程无实数根,则的取值范围是其中正确的结论有( )
A、4,-1 B、 ,-1 C、4,0 D、 ,-12. 已知 , 均为关于x的函数,当 时,函数值分别为 , ,若对于实数a,当 时,都有 ,则称 , 为亲函数,则以下函数 和 是亲函数的是( )A、 , B、 , C、 , D、 ,3. 在平面直角坐标系中,如果点P的横坐标和纵坐标相等,则称点P为和谐点.例如点(1,1),(﹣ , ﹣),(﹣ , ﹣),…,都是和谐点.若二次函数y=ax2+4x+c(a≠0)的图象上有且只有一个和谐点( , ),当0≤x≤m时,函数y=ax2+4x+c﹣(a≠0)的最小值为﹣3,最大值为1,m的取值范围是( )A、m≤4 B、m≥2 C、2≤m≤4 D、2<m<44. 定义: ,若函数 ,则该函数的最大值为( )A、0 B、2 C、3 D、45. 新定义:在平面直角坐标系中,对于点和点 , 若满足时,;时, , 则称点是点的限变点.例如:点的限变点是 , 点的限变点是 . 若点在二次函数的图象上,则当时,其限变点的纵坐标的取值范围是( )A、 B、 C、 D、6. 定义:若点P(a,b)在函数y= 的图象上,将以a为二次项系数,b为一次项系数构造的二次函数y=ax2+bx称为函数y=的一个“派生函数”.例如:点(2, )在函数y= 的图象上,则函数y=2x2+x称为函数y= 的一个“派生函数”.现给出以下两个命题:(1)存在函数y= 的一个“派生函数”,其图象的对称轴在y轴的右侧;(2)函数y= 的所有“派生函数”的图象都经过同一点.下列判断正确的是( )A、命题(1)与命题(2)都是真命题 B、命题(1)与命题(2)都是假命题 C、命题(1)是假命题,命题(2)是真命题 D、命题(1)是真命题,命题(2)是假命题7. 抛物线与轴的一个交点为 , 与轴交于点 , 点是抛物线的顶点,对称轴为直线 , 其部分图象如图所示,则以下个结论:; , 是抛物线上的两个点,若 , 且 , 则;在轴上有一动点 , 当的值最小时,则点的坐标为;若关于的方程无实数根,则的取值范围是其中正确的结论有( ) A、个 B、个 C、个 D、个
A、个 B、个 C、个 D、个二、填空题
-
8. 定义:若x,y满足且(t为常数),则称点为“和谐点”.(1)、若是“和谐点”,则 .(2)、若双曲线存在“和谐点”,则k的取值范围为 .9. 定义[a,b,c]为二次函数y=ax2+bx+c(a≠0)的特征数,下面给出特征数为[2m,1-m,-1-m]的函数的一些结论:①当m≠0时,点(1,0)一定在函数的图象上;②当m>0时,函数图象截x轴所得的线段长度大于 ;③当m<0时,函数在 时,y随x的增大而减小;④当m>0,若抛物线的顶点与抛物线与x轴两交点组成的三角形为等腰直角三角形,则 ,正确的结论是.(填写序号)10. 抛物线(是常数,)经过三点,且 . 下列四个结论:
①;
②;
③当时,若点在该抛物线上,则;
④若关于的一元二次方程有两个相等的实数根,则 .
其中正确的是(填写序号).
三、解答题
-
11.
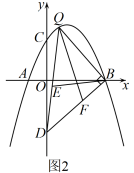
定义:如图1,抛物线 与 轴交于A,B两点,点P在抛物线上(点P与A,B两点不重合),如果△ABP的三边满足 ,则称点P为抛物线 的勾股点。
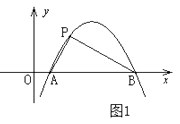
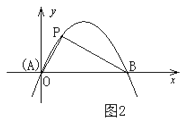 (1)、直接写出抛物线 的勾股点的坐标;(2)、如图2,已知抛物线C: 与 轴交于A,B两点,点P(1, )是抛物线C的勾股点,求抛物线C的函数表达式;(3)、在(2)的条件下,点Q在抛物线C上,求满足条件 的点Q(异于点P)的坐标
(1)、直接写出抛物线 的勾股点的坐标;(2)、如图2,已知抛物线C: 与 轴交于A,B两点,点P(1, )是抛物线C的勾股点,求抛物线C的函数表达式;(3)、在(2)的条件下,点Q在抛物线C上,求满足条件 的点Q(异于点P)的坐标四、实践探究题
-
12. 定义:对角线互相垂直且相等的四边形叫做垂等四边形.
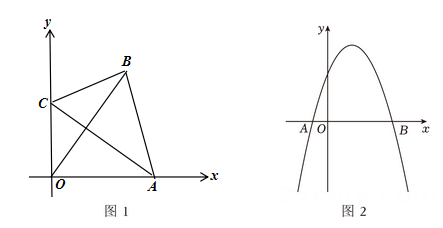 (1)、理解应用:如图,在平面直角坐标系xOy中,已知四边形OABC是垂等四边形,点A的坐标为(4,0),点C的坐标为(0,3),则点B的坐标为 .(2)、综合探究:如图,已知抛物线y=﹣x2+2x+3与x轴交于A,B两点,点A在点B的左侧,C,D两点在该抛物线上.若以A,B,C,D为顶点的四边形是垂等四边形.设点C的横坐标为m,点D的横坐标为n,且m>n,求m的值.13. 综合与实践
(1)、理解应用:如图,在平面直角坐标系xOy中,已知四边形OABC是垂等四边形,点A的坐标为(4,0),点C的坐标为(0,3),则点B的坐标为 .(2)、综合探究:如图,已知抛物线y=﹣x2+2x+3与x轴交于A,B两点,点A在点B的左侧,C,D两点在该抛物线上.若以A,B,C,D为顶点的四边形是垂等四边形.设点C的横坐标为m,点D的横坐标为n,且m>n,求m的值.13. 综合与实践中国旅游研究院2024年1月5日发布的“2024年冰雪旅游十佳城市”中,哈尔滨位列榜首,火爆出圈,其中帽儿山的滑雪运动深受欢迎.滑雪爱好者小李为了得出滑行距离(单位:m)与滑行时间(单位:s)之间的关系,以便更好地享受此项运动所带来的乐趣,他在滑道A上设置了若干个观测点,收集一些数据,如下表所示:
点位1
点位2
点位3
点位4
点位5
点位6
点位7
滑行时间
0
0.5
1
1.5
2
2.5
3
…
滑行距离
0
1.625
4.5
8.625
14
20.625
28.5
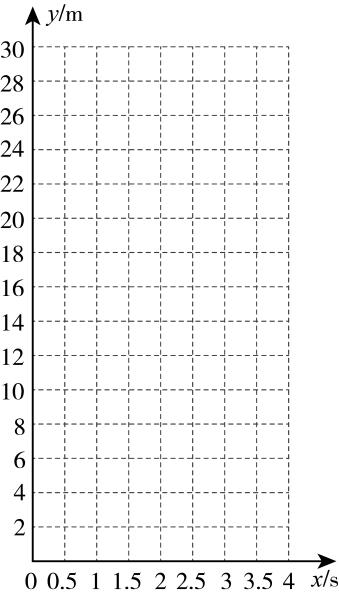 (1)、请你在平面直角坐标系中描出表中数据所对应的7个点,并用平滑的曲线连接它们;(2)、观察由(1)所得的图象,请你依图象选用一个函数近似地表示与之间的函数关系,并求出这个近似函数的关系式(不要求写出自变量的取值范围);(3)、若另一名滑雪爱好者小张在小李出发5秒后沿着滑道B滑行(两条滑道互相平行,且起点在同一直线上),他的滑行距离(单位:m)与滑行时间(单位:s)可近似地看成二次函数 , 当小李滑行距离为384m时,他比小张多滑行的距离不超过160m,求的最小值.(参考数据:)14. 规定:若函数的图像与函数的图像有三个不同的公共点,则称这两个函数互为“兄弟函数”,其公共点称为“兄弟点”.(1)、下列三个函数①;②;③ , 其中与二次函数互为“兄弟函数”的是(填写序号);(2)、若函数与互为“兄弟函数”,是其中一个“兄弟点”的横坐标.
(1)、请你在平面直角坐标系中描出表中数据所对应的7个点,并用平滑的曲线连接它们;(2)、观察由(1)所得的图象,请你依图象选用一个函数近似地表示与之间的函数关系,并求出这个近似函数的关系式(不要求写出自变量的取值范围);(3)、若另一名滑雪爱好者小张在小李出发5秒后沿着滑道B滑行(两条滑道互相平行,且起点在同一直线上),他的滑行距离(单位:m)与滑行时间(单位:s)可近似地看成二次函数 , 当小李滑行距离为384m时,他比小张多滑行的距离不超过160m,求的最小值.(参考数据:)14. 规定:若函数的图像与函数的图像有三个不同的公共点,则称这两个函数互为“兄弟函数”,其公共点称为“兄弟点”.(1)、下列三个函数①;②;③ , 其中与二次函数互为“兄弟函数”的是(填写序号);(2)、若函数与互为“兄弟函数”,是其中一个“兄弟点”的横坐标.①求实数a的值;
②直接写出另外两个“兄弟点”的横坐标是 ▲ 、 ▲ ;
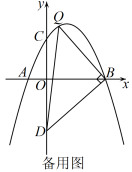
(3)、若函数(m为常数)与互为“兄弟函数”,三个“兄弟点”的横坐标分别为、、 , 且 , 求的取值范围.15. 《函数的图象与性质》拓展学习片段展示: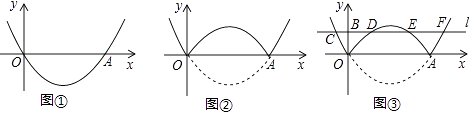 (1)、【问题】如图①,在平面直角坐标系中,抛物线y=a(x﹣2)2﹣ 经过原点O,与x轴的另一个交点为A,则a= .
(1)、【问题】如图①,在平面直角坐标系中,抛物线y=a(x﹣2)2﹣ 经过原点O,与x轴的另一个交点为A,则a= .
(2)、【操作】将图①中抛物线在x轴下方的部分沿x轴折叠到x轴上方,将这部分图象与原抛物线剩余部分的图象组成的新图象记为G,如图②.直接写出图象G对应的函数解析式.(3)、【探究】在图②中,过点B(0,1)作直线l平行于x轴,与图象G的交点从左至右依次为点C,D,E,F,如图③.求图象G在直线l上方的部分对应的函数y随x增大而增大时x的取值范围.(4)、【应用】P是图③中图象G上一点,其横坐标为m,连接PD,PE.直接写出△PDE的面积不小于1时m的取值范围.五、综合题
-
16. 定义:若一个函数图象上存在横、纵坐标相等的点,则称该点为这个函数图象的“等值点”.例如,点 是函数 的图象的“等值点”.(1)、分别判断函数 的图象上是否存在“等值点”?如果存在,求出“等值点”的坐标;如果不存在,说明理由;(2)、设函数 的图象的“等值点”分别为点A,B,过点B作 轴,垂足为C.当 的面积为3时,求b的值;(3)、若函数 的图象记为 ,将其沿直线 翻折后的图象记为 .当 两部分组成的图象上恰有2个“等值点”时,直接写出m的取值范围.17. 我们约定:若关于x的二次函数与同时满足 , 则称函数与函数互为“美美与共”函数.根据该约定,解答下列问题:(1)、若关于x的二次函数与互为“美美与共”函数,求k,m,n的值;(2)、对于任意非零实数r,s,点与点始终在关于x的函数的图像上运动,函数与互为“美美与共”函数.
①求函数的图像的对称轴;
②函数的图像是否经过某两个定点?若经过某两个定点,求出这两个定点的坐标;否则,请说明理由;
(3)、在同一平面直角坐标系中,若关于x的二次函数与它的“美美与共”函数的图像顶点分别为点A,点B,函数的图像与x轴交于不同两点C,D,函数的图像与x轴交于不同两点E,F.当时,以A,B,C,D为顶点的四边形能否为正方形?若能,求出该正方形面积的取值范围;若不请说明理由.18. 如图1,在平面直角坐标系中,已知二次函数的图象与x轴交于点 , , 与轴交于点 .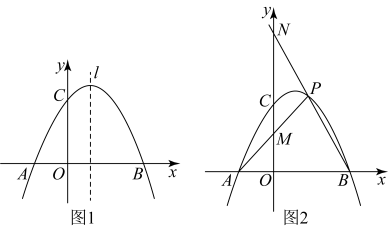 (1)、求抛物线的解析式;(2)、已知为抛物线上一点,为抛物线对称轴上一点,以 , , 为顶点的三角形是等腰直角三角形,且 , 求出点的坐标;(3)、如图 , 为第一象限内抛物线上一点,连接交轴于点 , 连接并延长交轴于点 , 在点运动过程中,是否为定值?若是,求出这个定值;若不是,请说明理由.19. 如图1,在平面直角坐标系 中,抛物线 与x轴分别相交于A、B两点,与y轴相交于点C,下表给出了这条抛物线上部分点 的坐标值:
(1)、求抛物线的解析式;(2)、已知为抛物线上一点,为抛物线对称轴上一点,以 , , 为顶点的三角形是等腰直角三角形,且 , 求出点的坐标;(3)、如图 , 为第一象限内抛物线上一点,连接交轴于点 , 连接并延长交轴于点 , 在点运动过程中,是否为定值?若是,求出这个定值;若不是,请说明理由.19. 如图1,在平面直角坐标系 中,抛物线 与x轴分别相交于A、B两点,与y轴相交于点C,下表给出了这条抛物线上部分点 的坐标值:x
…
0
1
2
3
…
y
…
0
3
4
3
0
…
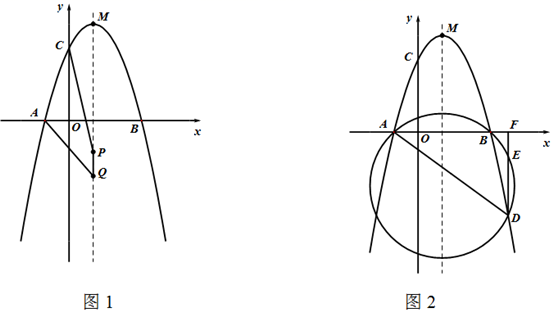 (1)、求出这条抛物线的解析式及顶点M的坐标;(2)、 是抛物线对称轴上长为1的一条动线段(点P在点Q上方),求 的最小值;(3)、如图2,点D是第四象限内抛物线上一动点,过点D作 轴,垂足为F, 的外接圆与 相交于点E.试问:线段 的长是否为定值?如果是,请求出这个定值;如果不是,请说明理由.20. 如图,在平面直角坐标系中,四边形 为正方形,点 , 在 轴上,抛物线 经过点 , 两点,且与直线 交于另一点 .
(1)、求出这条抛物线的解析式及顶点M的坐标;(2)、 是抛物线对称轴上长为1的一条动线段(点P在点Q上方),求 的最小值;(3)、如图2,点D是第四象限内抛物线上一动点,过点D作 轴,垂足为F, 的外接圆与 相交于点E.试问:线段 的长是否为定值?如果是,请求出这个定值;如果不是,请说明理由.20. 如图,在平面直角坐标系中,四边形 为正方形,点 , 在 轴上,抛物线 经过点 , 两点,且与直线 交于另一点 . (1)、求抛物线的解析式;(2)、 为抛物线对称轴上一点, 为平面直角坐标系中的一点,是否存在以点 , , , 为顶点的四边形是以 为边的菱形.若存在,请求出点 的坐标;若不存在,请说明理由;(3)、 为 轴上一点,过点 作抛物线对称轴的垂线,垂足为 ,连接 , .探究 是否存在最小值.若存在,请求出这个最小值及点 的坐标;若不存在,请说明理由.21. 已知抛物线与x轴交于两点,与y轴交于点 , 点P为第一象限抛物线上的点,连接 .
(1)、求抛物线的解析式;(2)、 为抛物线对称轴上一点, 为平面直角坐标系中的一点,是否存在以点 , , , 为顶点的四边形是以 为边的菱形.若存在,请求出点 的坐标;若不存在,请说明理由;(3)、 为 轴上一点,过点 作抛物线对称轴的垂线,垂足为 ,连接 , .探究 是否存在最小值.若存在,请求出这个最小值及点 的坐标;若不存在,请说明理由.21. 已知抛物线与x轴交于两点,与y轴交于点 , 点P为第一象限抛物线上的点,连接 .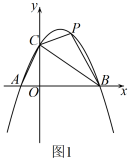
 (1)、直接写出结果; , , 点A的坐标为 , ;(2)、如图1,当时,求点P的坐标;(3)、如图2,点D在y轴负半轴上, , 点Q为抛物线上一点, , 点E,F分别为的边上的动点, , 记的最小值为m.
(1)、直接写出结果; , , 点A的坐标为 , ;(2)、如图1,当时,求点P的坐标;(3)、如图2,点D在y轴负半轴上, , 点Q为抛物线上一点, , 点E,F分别为的边上的动点, , 记的最小值为m.①求m的值;
②设的面积为S,若 , 请直接写出k的取值范围.
22. 在平面直角坐标系中,如果点的横坐标和纵坐标相等,则称点为和谐点,例如:点 , , , ……都是和谐点.(1)、判断函数的图象上是否存在和谐点,若存在,求出其和谐点的坐标;(2)、若二次函数的图象上有且只有一个和谐点 .①求 , 的值;
②若时,函数的最小值为-1,最大值为3,求实数的取值范围.
23. 定义:由两条与x轴有着相同的交点,并且开口方向相同的抛物线所围成的封闭曲线称为“月牙线”,如图①,抛物线C1:y=x2+2x﹣3与抛物线C2:y=ax2+2ax+c组成一个开口向上的“月牙线”,抛物线C1和抛物线C2与x轴有着相同的交点A(﹣3,0)、B(点B在点A右侧),与y轴的交点分别为G、H(0,﹣1).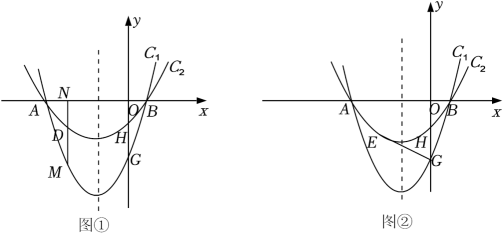 (1)、求抛物线C2的解析式和点G的坐标.(2)、点M是x轴下方抛物线C1上的点,过点M作MN⊥x轴于点N,交抛物线C2于点D,求线段MN与线段DM的长度的比值.(3)、如图②,点E是点H关于抛物线对称轴的对称点,连接EG,在x轴上是否存在点F,使得△EFG是以EG为腰的等腰三角形?若存在,请求出点F的坐标;若不存在,请说明理由.24. 【发现问题】
(1)、求抛物线C2的解析式和点G的坐标.(2)、点M是x轴下方抛物线C1上的点,过点M作MN⊥x轴于点N,交抛物线C2于点D,求线段MN与线段DM的长度的比值.(3)、如图②,点E是点H关于抛物线对称轴的对称点,连接EG,在x轴上是否存在点F,使得△EFG是以EG为腰的等腰三角形?若存在,请求出点F的坐标;若不存在,请说明理由.24. 【发现问题】小明在练习簿的横线上取点为圆心,相邻横线的间距为半径画圆,然后半径依次增加一个间距画同心圆,描出了同心圆与横线的一些交点,如图1所示,他发现这些点的位置有一定的规律.
【提出问题】
小明通过观察,提出猜想:按此步骤继续画圆描点,所描的点都在某二次函数图象上.


 (1)、【分析问题】
(1)、【分析问题】小明利用已学知识和经验,以圆心为原点,过点的横线所在直线为轴,过点且垂直于横线的直线为轴,相邻横线的间距为一个单位长度,建立平面直角坐标系,如图2所示.当所描的点在半径为5的同心圆上时,其坐标为 .
(2)、【解决问题】请帮助小明验证他的猜想是否成立.
(3)、【深度思考】小明继续思考:设点 , 为正整数,以为直径画 , 是否存在所描的点在上.若存在,求的值;若不存在,说明理由.
25. 新定义:我们把抛物线(其中)与抛物线称为“关联抛物线”.例如:抛物线的“关联抛物线”为:.已知抛物线的“关联抛物线”为.(1)、写出的解析式(用含a的式子表示)及顶点坐标;(2)、若 , 过x轴上一点P,作x轴的垂线分别交抛物线 , 于点M,N.①当时,求点a的坐标;
②当时,的最大值与最小值的差为 , 求a的值.
26. 【生活情境】为美化校园环境,某学校根据地形情况,要对景观带中一个长 , 宽的长方形水池进行加长改造(如图①,改造后的水池仍为长方形,以下简称水池1),同时,再建造一个周长为的矩形水池(如图②,以下简称水池2).

【建立模型】
如果设水池的边加长长度为 , 加长后水池1的总面积为 , 则关于的函数解析式为:;设水池2的边的长为 , 面积为 , 则关于的函数解析式为: , 上述两个函数在同一平面直角坐标系中的图像如图③.

【问题解决】
(1)、若水池2的面积随长度的增加而减小,则长度的取值范围是(可省略单位),水池2面积的最大值是;(2)、在图③字母标注的点中,表示两个水池面积相等的点是 , 此时的值是;(3)、当水池1的面积大于水池2的面积时,的取值范围是;(4)、在范围内,求两个水池面积差的最大值和此时的值;(5)、假设水池的边的长度为 , 其他条件不变(这个加长改造后的新水池简称水池3),则水池3的总面积关于的函数解析式为: . 若水池3与水池2的面积相等时,有唯一值,求的值.27. 定义:点P(m,m)是平面直角坐标系内一点,将函数l的图象位于直线x=m左侧部分,以直线y=m为对称轴翻折,得到新的函数l′的图象,我们称函数l′的函数是函数l的相关函数,函数l′的图象记作F1 , 函数l的图象未翻折的部分记作F2 , 图象F1和F2合起来记作图象F.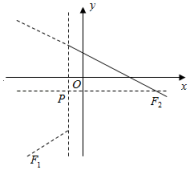
例如:函数l的解析式为y=x2﹣1,当m=1时,它的相关函数l′的解析式为y=﹣x2+3(x<1).
(1)、如图,函数l的解析式为y=﹣x+2,当m=﹣1时,它的相关函数l′的解析式为y= .(2)、函数l的解析式为y=﹣ , 当m=0时,图象F上某点的纵坐标为﹣2,求该点的横坐标.(3)、已知函数l的解析式为y=x2﹣4x+3,①已知点A、B的坐标分别为(0,2)、(6,2),图象F与线段AB只有一个公共点时,结合函数图象,求m的取值范围;
②若点C(x,n)是图象F上任意一点,当m﹣2≤x≤5时,n的最小值始终保持不变,求m的取值范围(直接写出结果).
28. 如果关于x的一元二次方程 有两个实数根,且其中一个根为另一个根的 倍,则称这样的方程为“k系方程”.如方程 的两根分别为: ,则方程 为“2系方程”.(1)、下列方程是“3系方程”的是(填序号即可);① ;② ;③ .
(2)、若关于x的一元二次方程 是“2系方程”.①求证: ;
②若 ,且关于x的函数 ,当 时的最大值为1,求a的值.
-