广东省惠州市惠阳区城乡教育共同体(第五组)2023-2024学年八年级下学期数学期中联考试卷
试卷更新日期:2024-05-07 类型:期中考试
一、单选题(每题3分,共30分)
-
1. 要使 有意义,则实数x的取值范围是( )A、 B、 且 C、 且 D、2. 与 是同类二次根式的是( )A、 B、 C、 D、3. 下列四组线段中,可以构成直角三角形的是( )A、4,5,6 B、2,3,4 C、 ,3,4 D、1, ,34. 直角三角形的斜边长为6cm,则斜边上的中线长为( )A、2cm B、2.5cm C、3cm D、4cm5. 如图,在平面直角坐标系中,菱形的顶点在轴上,顶点在轴上,且的坐标分别是 , 则顶点的坐标是( )
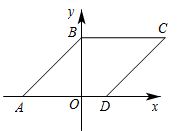 A、 B、 C、 D、6. 如图,中,平分交于E , 若 , 则度数为( )
A、 B、 C、 D、6. 如图,中,平分交于E , 若 , 则度数为( ) A、 B、 C、 D、7. 如图,将矩形ABCD沿对角线AC折叠,点D落在点E处,AE与边BC的交点为M . 已知:AB=1,BC=2,则BM的长等于( )
A、 B、 C、 D、7. 如图,将矩形ABCD沿对角线AC折叠,点D落在点E处,AE与边BC的交点为M . 已知:AB=1,BC=2,则BM的长等于( ) A、 B、 C、 D、8. 如图,在平行四边形中,对角线 , 相交于点 , 下列条说法不正确的是( )
A、 B、 C、 D、8. 如图,在平行四边形中,对角线 , 相交于点 , 下列条说法不正确的是( ) A、 B、 C、 D、9. 如图,在边长为7的正方形中,为边上一点,为边上一点,连接、 , 将沿折叠,使点恰好落在边上的处,若 , 则的长度为( )
A、 B、 C、 D、9. 如图,在边长为7的正方形中,为边上一点,为边上一点,连接、 , 将沿折叠,使点恰好落在边上的处,若 , 则的长度为( ) A、 B、 C、 D、210. 如图,矩形中, , 点G是边上的一点,点P是边上的一个动点,连接 , , 点E , F分别是 , 的中点,在点P的运动过程中,的最大长度为( )
A、 B、 C、 D、210. 如图,矩形中, , 点G是边上的一点,点P是边上的一个动点,连接 , , 点E , F分别是 , 的中点,在点P的运动过程中,的最大长度为( ) A、5 B、6 C、8 D、不能确定
A、5 B、6 C、8 D、不能确定二、填空题(每题4分,共28分)
-
11. “矩形的对角线相等”的逆命题为 , 该逆命题是命题(真、假)12. 若 , 则=.13. 如下图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为 , 则正方形A , B , C , D的面积之和为.
 14. 如图,从一个大正方形中裁去两个小正方形,则留下部分的面积为 .
14. 如图,从一个大正方形中裁去两个小正方形,则留下部分的面积为 . 15. 对于任意不相等的两个实数 , ,新定义一种运算“※”如下: ※ ,则2※ .16. 如图,在一张矩形纸片ABCD中,AD=4cm,点E,F分别是CD和AB的中点,现将这张纸片折叠,使点B落在EF上的点G处,折痕为AH,若HG延长线恰好经过点D,则CD的长为.
15. 对于任意不相等的两个实数 , ,新定义一种运算“※”如下: ※ ,则2※ .16. 如图,在一张矩形纸片ABCD中,AD=4cm,点E,F分别是CD和AB的中点,现将这张纸片折叠,使点B落在EF上的点G处,折痕为AH,若HG延长线恰好经过点D,则CD的长为. 17. 如图,在直角坐标系中,四边形是正方形, , , , . 曲线、、叫做“正方形的渐开线”,其中弧、弧、弧、弧、的圆心依次是点、、、循环,则点的坐标是 .
17. 如图,在直角坐标系中,四边形是正方形, , , , . 曲线、、叫做“正方形的渐开线”,其中弧、弧、弧、弧、的圆心依次是点、、、循环,则点的坐标是 .
三、解答题(每题6分,共18分)
-
18. 计算: .19. 如图,在△ABC中,CD⊥AB,垂足为D.AD=1,BD=4,CD=2.求证:∠ACB=90°.
 20. 如图所示,已知平行四边形ABCD的对角线交于O,过O作直线交AB、CD的反向延长线于E、F,求证:OE=OF.
20. 如图所示,已知平行四边形ABCD的对角线交于O,过O作直线交AB、CD的反向延长线于E、F,求证:OE=OF.
四、解答题(每题8分,共24分)
-
21. , , 求下列代数式的值.(1)、(2)、22. 如图是某货站传送货物的平面示意图,为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角,使其由改为 . 已知原传送带AB长为 .
 (1)、新传送带;(2)、如果需要在货物着地点C的左侧留出的通道,试判断与B点距离为的货物是否需要挪走,并说明理由.23. 如图,四边形 是平行四边形, ,垂足分别为 ,且 .
(1)、新传送带;(2)、如果需要在货物着地点C的左侧留出的通道,试判断与B点距离为的货物是否需要挪走,并说明理由.23. 如图,四边形 是平行四边形, ,垂足分别为 ,且 .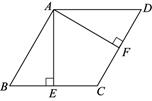 (1)、求证:四边形 是菱形;(2)、连接EF并延长,交AD的延长线于点G,若 ,求EG的长.
(1)、求证:四边形 是菱形;(2)、连接EF并延长,交AD的延长线于点G,若 ,求EG的长.五、解答题(每题10分,共20分)
-
24. 阅读下列材料,然后回答问题.在进行二次根式的化简与运算时,我们有时会碰上如一样的式子,其实我们还可以将其进一步化简:
(一),
(二),
(三)
以上这种化简的步骤叫做分母有理化.
还可以用以下方法化简:(四)
(1)、直接写出化简结果① , ② .(2)、请选择适当的方法化简 .(3)、化简: .25. 如图,在中, , 过点A作交于点D , . 动点P从点B出发(点P不与点A、点D重合),沿折线向终点D运动,在边上运动时速度为每秒1个单位长度,在边上运动时速度为每秒2个单位长度,设点P的运动时间为t秒(). (1)、线段的长为;当点P在边上运动时(用含t的式子表示);(2)、当时, ; ;(3)、若点P运动到的角平分线上时,直接写出线段的长;(4)、在整个运动过程中,当与的一边垂直时,直接写出此时t的值.
(1)、线段的长为;当点P在边上运动时(用含t的式子表示);(2)、当时, ; ;(3)、若点P运动到的角平分线上时,直接写出线段的长;(4)、在整个运动过程中,当与的一边垂直时,直接写出此时t的值.