广东省深圳市宝安区2023-2024学年七年级下学期数学期中试卷
试卷更新日期:2024-05-07 类型:期中考试
一、选择题(每小题3分,共30分,每小题有四个选项,其中只有一个是正确的,请把答案按要求填涂到答题卡相应位置上)
-
1. 经科学家研究,冠状病毒多数为球形或近似球形,其直径约为 米,若用科学记数法表示正确的结果是( ).A、 米 B、 米 C、 米 D、 米2. 下列计算正确的是( )A、 B、 C、 D、3. 下列各图中,与是同位角的是( )A、
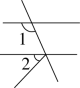 B、
B、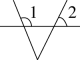 C、
C、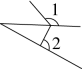 D、
D、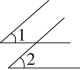 4. 如图,现要从村庄A修建一条连接公路的最短小路,过点A作于点H , 沿修建公路,这样做的理由是( )
4. 如图,现要从村庄A修建一条连接公路的最短小路,过点A作于点H , 沿修建公路,这样做的理由是( ) A、两点之间,线段最短 B、垂线段最短 C、过一点有且只有一条直线与已知直线垂直 D、两点确定一条直线5. 如图,将三角板的直角顶点放在直尺的一边上,如果 , 那么的度数为( )
A、两点之间,线段最短 B、垂线段最短 C、过一点有且只有一条直线与已知直线垂直 D、两点确定一条直线5. 如图,将三角板的直角顶点放在直尺的一边上,如果 , 那么的度数为( ) A、 B、 C、 D、6. 在△ABC中,作出AC边上的高,正确的是( ).A、
A、 B、 C、 D、6. 在△ABC中,作出AC边上的高,正确的是( ).A、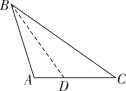 B、
B、 C、
C、 D、
D、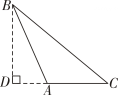 7. 有一张直角三角形纸片,记作 , 其中 , 按如图方式剪去它的一个角(虚线部分),在剩下的四边形中,则、满足的等量关系为( )
7. 有一张直角三角形纸片,记作 , 其中 , 按如图方式剪去它的一个角(虚线部分),在剩下的四边形中,则、满足的等量关系为( ) A、 B、 C、 D、8. 弹簧挂上物体后会伸长,测得一弹簧的长度与所挂的物体的质量间有下面的关系:
A、 B、 C、 D、8. 弹簧挂上物体后会伸长,测得一弹簧的长度与所挂的物体的质量间有下面的关系:0
1
2
3
4
5
10
11
12
下列说法错误的是( )
A、x与y都是变量,且x是自变量,y是因变量 B、弹簧不挂重物时的长度为 C、当时,物体质量每增加 , 弹簧长度y增加 D、当时,x与y满足的关系式是9. 如图1,图2,点C是上一点,利用尺规过点C作 , 下列说法错误的是( ) A、图1的原理是同位角相等,两直线平行 B、以点E为圆心,以为半径作弧,得到弧 C、图2的原理是两直线平行,内错角相等 D、以点C为圆心,以为半径作弧,得到弧10. 我国宋代数学家杨辉所著《解答九章算法》中记载了用如图所示的三角形解释了二项和的乘方展开式中的系数规律,我们把这种数字三角形叫做“杨辉三角”.请你利用杨辉三角,计算的展开式中,含项的系数是( )
A、图1的原理是同位角相等,两直线平行 B、以点E为圆心,以为半径作弧,得到弧 C、图2的原理是两直线平行,内错角相等 D、以点C为圆心,以为半径作弧,得到弧10. 我国宋代数学家杨辉所著《解答九章算法》中记载了用如图所示的三角形解释了二项和的乘方展开式中的系数规律,我们把这种数字三角形叫做“杨辉三角”.请你利用杨辉三角,计算的展开式中,含项的系数是( ) A、1 B、5 C、16 D、80
A、1 B、5 C、16 D、80二、填空题(每小题3分,共15分,请把答案填到答题卷相应位置上)
-
11. 一个角的余角是这个角的2倍,则这个角的度数°.12. 若长度分别为a , 2,5的三条线段能组成一个等腰三角形,则 .13. 若 , 则= .14. 如图,在中,已知点D、E、F分别为边、、的中点,且阴影部分图形面积等于4平方厘米,则的面积为平方厘米
 15. 如图①是长方形纸带,∠CFE=55°,将纸带沿EF折叠成图②,再沿GE折叠成图③,则图③中∠DEF的度数是.
15. 如图①是长方形纸带,∠CFE=55°,将纸带沿EF折叠成图②,再沿GE折叠成图③,则图③中∠DEF的度数是.
三、解答题(共55分)
-
16.(1)、(2)、17. 先化简,再求值: , 其中x=1,y=2.18. 如图, , , 求证: .

证明:∵(已知),
∴ ▲ , ( )
∵(已知),
∴ ▲ (同角的补角相等)
∴ ▲ ▲ , (内错角相等,两直线平行)
∴( ).
19. 如图所示,在中,是角平分线,是高. (1)、若 , 求:①的度数;②的度数.(2)、已知 , 则(用表示).20. 如图, , 两地相距50千米,甲于某日下午1时骑自行车从地出发骑往地,图中的折线和线段分别表示甲与乙所行驶的路程和时间的关系.根据图象回答下列问题:
(1)、若 , 求:①的度数;②的度数.(2)、已知 , 则(用表示).20. 如图, , 两地相距50千米,甲于某日下午1时骑自行车从地出发骑往地,图中的折线和线段分别表示甲与乙所行驶的路程和时间的关系.根据图象回答下列问题: (1)、甲出发小时,乙才开始出发;(2)、乙比甲早到小时;(3)、甲从下午2时到5时的平均速度是千米/小时;乙的平均速度是千米/小时;(4)、请你根据图象上的数据,求乙出发后用多长时间就追上甲?21. 数形结合是数学学习中一种重要的方法,我们可以利用几何图形验证乘法公式.如图1,用一张边长为a的正方形纸片减去一个边长为b的正方形,剩下部分通过剪拼可以得到一个新的长方形(图2),请你完成下面的探究:
(1)、甲出发小时,乙才开始出发;(2)、乙比甲早到小时;(3)、甲从下午2时到5时的平均速度是千米/小时;乙的平均速度是千米/小时;(4)、请你根据图象上的数据,求乙出发后用多长时间就追上甲?21. 数形结合是数学学习中一种重要的方法,我们可以利用几何图形验证乘法公式.如图1,用一张边长为a的正方形纸片减去一个边长为b的正方形,剩下部分通过剪拼可以得到一个新的长方形(图2),请你完成下面的探究: (1)、比较两图的阴影部分面积,可以得到乘法公式(用表示);(2)、若 , 请你画一个几何图形,证明 , 并根据你画的图形,直接写出正确的展开结果.(3)、计算 .22. 阅读理解:如图1,已知点A是外一点,连接 , . 求的度数.
(1)、比较两图的阴影部分面积,可以得到乘法公式(用表示);(2)、若 , 请你画一个几何图形,证明 , 并根据你画的图形,直接写出正确的展开结果.(3)、计算 .22. 阅读理解:如图1,已知点A是外一点,连接 , . 求的度数. (1)、阅读并补充下面推理过程.
(1)、阅读并补充下面推理过程.解:过点A作 , ∴ , .
∵ .
∴ .
解题反思:从上面的推理过程中,我们发现平行线具有“等角转化”的功能,将 “凑”在一起,得出角之间的关系,使问题得以解决.
 (2)、方法运用:如图2,已知 , 求的度数.(3)、深化拓展:如图3,已知 , 点C在点D的右侧, , 平分 , 点B是直线上的一个动点(不与点A重合), , 平分 , , 所在的直线交于点E , 点E在与两条平行线之间.若 , 请你求出的度数.(用含n的代数式表示)
(2)、方法运用:如图2,已知 , 求的度数.(3)、深化拓展:如图3,已知 , 点C在点D的右侧, , 平分 , 点B是直线上的一个动点(不与点A重合), , 平分 , , 所在的直线交于点E , 点E在与两条平行线之间.若 , 请你求出的度数.(用含n的代数式表示)