湖北省荆楚初中联盟2023-2024学年七年级下学期期中数学试题
试卷更新日期:2024-05-06 类型:期中考试
一、选择题(共10题,每题3分,共30分.在每题给出的四个选项中,只有一个选项符合题目要求)
-
1. 下列各数中是无理数的是( )A、 B、 C、 D、3.142. 下列四个图形中,与是对顶角的是()A、
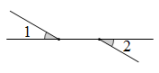 B、
B、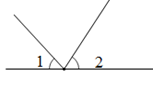 C、
C、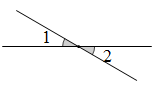 D、
D、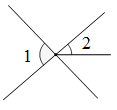 3. 下列说法正确的是( )A、5是-25的算术平方根 B、的算术平方根是-4 C、0的平方根与算术平方根都是0 D、的平方根是4. 若点在y轴上,则点M的坐标是( )A、 B、 C、 D、5. 一个正方体的体积扩大为原来的8倍,它的棱长变为原来的( )倍A、2 B、3 C、4 D、86. 课间操时,小钦、小新、小敏的位置如图所示,小钦对小敏说:“如果我的位置用表示,小新的位置用表示,那么你的位置可以表示成( )”
3. 下列说法正确的是( )A、5是-25的算术平方根 B、的算术平方根是-4 C、0的平方根与算术平方根都是0 D、的平方根是4. 若点在y轴上,则点M的坐标是( )A、 B、 C、 D、5. 一个正方体的体积扩大为原来的8倍,它的棱长变为原来的( )倍A、2 B、3 C、4 D、86. 课间操时,小钦、小新、小敏的位置如图所示,小钦对小敏说:“如果我的位置用表示,小新的位置用表示,那么你的位置可以表示成( )” A、 B、 C、 D、7. 如图, , CD与AF交于点G , , 则的度数是( )
A、 B、 C、 D、7. 如图, , CD与AF交于点G , , 则的度数是( ) A、60° B、80° C、100° D、120°8. 如图,以单位长度为边长画一个正方形,以原点为圆心,正方形的对角线长为半径画弧,与正半轴的交点表示的数为a , 则a是( )
A、60° B、80° C、100° D、120°8. 如图,以单位长度为边长画一个正方形,以原点为圆心,正方形的对角线长为半径画弧,与正半轴的交点表示的数为a , 则a是( ) A、2的平方根 B、2的算术平方根 C、2的立方根 D、不能确定9. 如图,一块长为a米,宽为b米的长方形草地上,有一条弯曲的小路,小路左边线向右平移t米就是它的边线.若 , , 则小路面积与绿地面积的比为( )
A、2的平方根 B、2的算术平方根 C、2的立方根 D、不能确定9. 如图,一块长为a米,宽为b米的长方形草地上,有一条弯曲的小路,小路左边线向右平移t米就是它的边线.若 , , 则小路面积与绿地面积的比为( )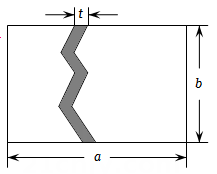 A、 B、 C、 D、10. 在平面直角坐标系中,对于点 , 我们把叫做点P的伴随点,已知的伴随点为 , 的伴随点为 , …,这样依次下去得到 , , ……, . 若的坐标为 , 则的坐标为( )A、 B、 C、 D、
A、 B、 C、 D、10. 在平面直角坐标系中,对于点 , 我们把叫做点P的伴随点,已知的伴随点为 , 的伴随点为 , …,这样依次下去得到 , , ……, . 若的坐标为 , 则的坐标为( )A、 B、 C、 D、二、填空题(共5题,每题3分,共15分)
-
11. 已知 , 则 .12. 若x轴上的点P到y轴的距离为3,则点P的坐标为 .13. 一个正数x的平方根是与 , 则 .14. 在正实数范围内定义一种运算“”:当时,;当时, . 则方程的解是 .15. 如图, , 将一副直角三角板作如下摆放, , . 下列结论:①;②;③;④ . 其中正确结论的序号是 .

三、解答题(共9题,共75分,解答应写出文字说明、证明过程或演算步骤.)
-
16. 计算:(1)、;(2)、 .17. 求下列各式中的x的值:(1)、(2)、18. 如图,直线AB , CD相交于点O , OA平分 .
 (1)、若 , 求的度数;(2)、若 , 求的度数.19. 填空,请依据条件进行推理,得出结论,并在括号内填上适当的依据.
(1)、若 , 求的度数;(2)、若 , 求的度数.19. 填空,请依据条件进行推理,得出结论,并在括号内填上适当的依据.如图,于F , 于E , , 求证: .

证明:∵ , (已知),
∴(_▲_).
∴(_▲_).
∴(_▲_).
∵(已知),
又∵(平角的定义),
∴_▲_(_▲_).
∴(_▲_).
∴(_▲_).
20. 如图(1)大正方形纸片,其面积为 . 小钦同学按如图的方法把大正方形沿对角线裁成四个三角形.然后再把这四个三角形拼成如图(2)两个相同的小正方形. (1)、求小正方形的边长;
(1)、求小正方形的边长;
(2)、小钦同学要在一个小正方形中沿边的方向裁出一个面积为的长方形,使它的长宽之比为 , 问能否成功,试说明理由.21. 如图,在中,AD平分交BC于点D , 点E在BA上,过点E的直线与CA的延长线交于点F , 与BC交于点G , . (1)、AD与EF平行吗?请说明理由;(2)、点N在AD上,若 , , , GN平分吗?请说明理由.22. 如图,在平面直角坐标系中,网格线的交点称为格点,每一个小正方形方格边长为1个单位长度,三角形ABC的三个顶点均在格点上,内任意一点经过平移后对应点为 , 将作同样的平移得到 , 点A , B、C平移后对应的点为、、 .
(1)、AD与EF平行吗?请说明理由;(2)、点N在AD上,若 , , , GN平分吗?请说明理由.22. 如图,在平面直角坐标系中,网格线的交点称为格点,每一个小正方形方格边长为1个单位长度,三角形ABC的三个顶点均在格点上,内任意一点经过平移后对应点为 , 将作同样的平移得到 , 点A , B、C平移后对应的点为、、 . (1)、请画出平移后的三角形 , 写出点的坐标为;(2)、四边形的面积是;(3)、在图中存在格点Q , 使得直线BQ将三角形ABC分成面积相等的两个三角形,则点Q的坐标是;
(1)、请画出平移后的三角形 , 写出点的坐标为;(2)、四边形的面积是;(3)、在图中存在格点Q , 使得直线BQ将三角形ABC分成面积相等的两个三角形,则点Q的坐标是;
(4)、若经过平移后对应点为 , 点A、C作同样的平移得到对应的点为、 . 此时长方形的面积为20,求出m和n的值.23. 已知, , 点E , F分别是AB , CD上的点,点M是平面内一点,连接EM , FM , , . (1)、如图1,FM与AB交于点K , 则°,°,°;(2)、如图2,点M在直线AB、CD之间,延长ME到G , 点H在EG的上方,连接GH , BH , 若 , 求的度数;(3)、如图3,P为直线AC上一动点,探究 , 和的数量关系,请直接给出结论.(提示:题中所有角都是大于0°小于180°的角)24. 在平面直角坐标系中, , , , 且 .
(1)、如图1,FM与AB交于点K , 则°,°,°;(2)、如图2,点M在直线AB、CD之间,延长ME到G , 点H在EG的上方,连接GH , BH , 若 , 求的度数;(3)、如图3,P为直线AC上一动点,探究 , 和的数量关系,请直接给出结论.(提示:题中所有角都是大于0°小于180°的角)24. 在平面直角坐标系中, , , , 且 . (1)、请直接写出点A , B , C的坐标;(2)、如图1,点在线段BC上,线段轴, , 点E从点D出发沿x轴负方向平移.
(1)、请直接写出点A , B , C的坐标;(2)、如图1,点在线段BC上,线段轴, , 点E从点D出发沿x轴负方向平移.①当线段BE最短时,求的面积;
②若 , 求点D的坐标.
(3)、如图2,若点是x轴上方一点,且 , 求m与n之间的关系式.(提示:)