【培优卷】北师大版数学八(下)第六章 平行四边形 章末检测
试卷更新日期:2024-05-05 类型:单元试卷
一、选择题(每题3分,共30分)
-
1. 一个多边形的每一个内角都等于140°,那么从这个多边形的一个顶点出发的对角线的条数是( )A、6条 B、7条 C、8条 D、9条2. 如图,将▱ABCD沿对角线BD折叠,使点A落在点E处,交BC于点F,若∠ABD=48°,∠CFD=40°,则∠E为
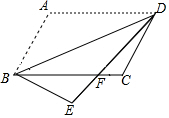 A、 B、 C、 D、3. 在四边形 ABCD中,对角线 AC,BD相交于点O,有下列条件:
A、 B、 C、 D、3. 在四边形 ABCD中,对角线 AC,BD相交于点O,有下列条件:①OA=OC,OB=OD;
②AD∥BC,AB∥DC;
③AB=DC,AD=BC;
④AB∥DC,AD=BC.
其中能判定四边形ABCD为平行四边形的是( )
A、①④ B、②③ C、①②③ D、②③④4. 如图,四边形中,为对角线, , , E , F分别是边 , 的中点,则的取值范围是( )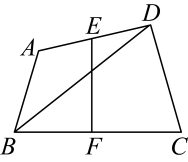 A、 B、 C、 D、5.
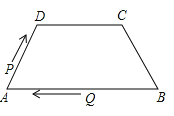
A、 B、 C、 D、5.如图,在四边形ABCD中,AB∥DC,AD=BC=5,DC=7,AB=13,点P从点A出发以3个单位/s的速度沿AD→DC向终点C运动,同时点Q从点B出发,以1个单位/s的速度沿BA向终点A运动.当四边形PQBC为平行四边形时,运动时间为( )
 A、4s B、3s C、2s D、1s6. 如图,一块长方形场地 的长 与宽 的比是 : , , ,垂足分别是 、 两点.现计划在四边形 区域种植花草,则四边形 与长方形 的面积比等于( )
A、4s B、3s C、2s D、1s6. 如图,一块长方形场地 的长 与宽 的比是 : , , ,垂足分别是 、 两点.现计划在四边形 区域种植花草,则四边形 与长方形 的面积比等于( ) A、1:3 B、2:3 C、1:2 D、1:47. 如图,在平行四边形中,对角线相交于点是对角线上的两点,给出下列四个条件:①;②;③;④ . 其中能判定四边形是平行四边形的有( )
A、1:3 B、2:3 C、1:2 D、1:47. 如图,在平行四边形中,对角线相交于点是对角线上的两点,给出下列四个条件:①;②;③;④ . 其中能判定四边形是平行四边形的有( ) A、① B、①④ C、①③④ D、①②③④8. 如图,在中, , , 平分 , 对角线相交于点O,连接 , 下列结论中正确的有( )
A、① B、①④ C、①③④ D、①②③④8. 如图,在中, , , 平分 , 对角线相交于点O,连接 , 下列结论中正确的有( )①;②;③;④;⑤
 A、2个 B、3个 C、4个 D、5个9. 如图1,用4个全等的正八边形进行拼接,使相邻的两个正八边形有一条公共边,围成一圈后中间形成一个正方形.用个全等的正五边形按这种方式拼接,如图2,若围成一圈后中间也形成一个正多边形,则的值为( )
A、2个 B、3个 C、4个 D、5个9. 如图1,用4个全等的正八边形进行拼接,使相邻的两个正八边形有一条公共边,围成一圈后中间形成一个正方形.用个全等的正五边形按这种方式拼接,如图2,若围成一圈后中间也形成一个正多边形,则的值为( ) A、6 B、8 C、10 D、1210. 如图,依次连接周长为1的小等边三角形各边的中点,得到第二个小等边三角形,再依次连接第二个小等边三角形各边的中点,得到第三个小等边三角形……按这样的规律,第2023个小等边三角形的周长为( )
A、6 B、8 C、10 D、1210. 如图,依次连接周长为1的小等边三角形各边的中点,得到第二个小等边三角形,再依次连接第二个小等边三角形各边的中点,得到第三个小等边三角形……按这样的规律,第2023个小等边三角形的周长为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每题3分,共15分)
-
11. 如图,点P是边长为1的菱形ABCD对角线AC上一个动点,点M、N分别是AB、BC边上的中点,则MP+NP的最小值是 .
 12. 如图,已知在△ABC 中,AB=4,AC=3,AD,AE分别是其角平分线和中线,过点 C 作CG⊥AD于点F,交 AB 于点 G,连结EF,则线段 EF 的长为.
12. 如图,已知在△ABC 中,AB=4,AC=3,AD,AE分别是其角平分线和中线,过点 C 作CG⊥AD于点F,交 AB 于点 G,连结EF,则线段 EF 的长为. 13. 如图是由射线AB,BC,CD,DE,EA组成的平面图形,则∠1+∠2+∠3+∠4+∠5= .
13. 如图是由射线AB,BC,CD,DE,EA组成的平面图形,则∠1+∠2+∠3+∠4+∠5= .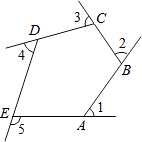 14. 如图,在平行四边形中, , , 是边延长线上一点,连接 , 以为边作等边三角形 , 连接 , 则的最小值是 .
14. 如图,在平行四边形中, , , 是边延长线上一点,连接 , 以为边作等边三角形 , 连接 , 则的最小值是 .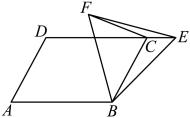 15. 如图,四边形中, , cm,cm,点P以1cm/s的速度由A点向B点运动,同时点Q以2cm/s的速度由C点向D点运动,其中一点到达终点时,另一点也停止运动,当线段将四边形截出一个平行四边形时,此时的运动时间为s.
15. 如图,四边形中, , cm,cm,点P以1cm/s的速度由A点向B点运动,同时点Q以2cm/s的速度由C点向D点运动,其中一点到达终点时,另一点也停止运动,当线段将四边形截出一个平行四边形时,此时的运动时间为s.
三、解答题(共10题,共75分)
-
16. 如图,在中,是的平分线.请仅用无刻度直尺分别按下列要求作图.(保留作图痕迹)
 (1)、在图(1)中,以为腰作一个等腰三角形;(2)、在图(2)中,以为边作 .17. 如图
(1)、在图(1)中,以为腰作一个等腰三角形;(2)、在图(2)中,以为边作 .17. 如图 (1)、如图1,求∠A+∠B+∠C+∠D+∠E+∠F+∠G的度数;(2)、如图2,求∠1+∠2+∠3+∠4+∠5+∠6的度数。18. 如图,在 ▱ ABCD中,AF 平分∠BAD,交 BC 于点F,CE平分∠BCD,交 AD于点 E.
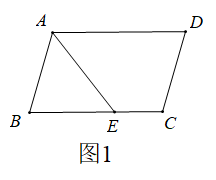
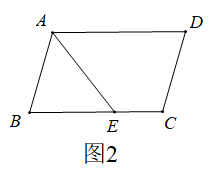
(1)、如图1,求∠A+∠B+∠C+∠D+∠E+∠F+∠G的度数;(2)、如图2,求∠1+∠2+∠3+∠4+∠5+∠6的度数。18. 如图,在 ▱ ABCD中,AF 平分∠BAD,交 BC 于点F,CE平分∠BCD,交 AD于点 E.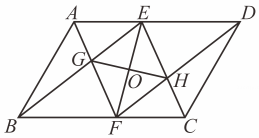 (1)、若AD=12,AB=8,求CF 的长.(2)、连结 BE,与 AF 相交于点 G,连结 DF,与CE 相交于点 H,连结 EF,GH 相交于点O.求证:EF 和GH 互相平分.19. 在中, , 分别是边 , 上的中线,与相交于点O .
(1)、若AD=12,AB=8,求CF 的长.(2)、连结 BE,与 AF 相交于点 G,连结 DF,与CE 相交于点 H,连结 EF,GH 相交于点O.求证:EF 和GH 互相平分.19. 在中, , 分别是边 , 上的中线,与相交于点O . (1)、如图1,M是中点,N是中点,
(1)、如图1,M是中点,N是中点,①求证:;
②求证:;
(2)、如图2,若 , 则 , , 之间的数量关系为 .20. (1)、用一条直线去截多边形,使得到的新多边形分别满足下列条件(在对应的图中画出图形,把截去的部分打上阴影):
(1)、用一条直线去截多边形,使得到的新多边形分别满足下列条件(在对应的图中画出图形,把截去的部分打上阴影):①在图1中,新多边形的内角和比原多边形的内角和增加了 180°.
②在图2中,新多边形的内角和与原多边形的内角和相等.
③在图3中,新多边形的内角和比原多边形的内角和减少了 180°.
(2)、若将一个多边形截去一个角后,得到的新多边形的内角和为 2 520°,求原多边形的边数.21. 如图1,在梯形中, , , , , , 点O是对角线的中点.点E为边上一动点,联结 . (1)、求的长;(2)、如果点E为边的中点,联结 , 求的面积;(3)、如图2,延长交射线于点F,联结 , 如果平分 , 求四边形的周长.22. 如图,在平面直角坐标系中,一次函数的图像与x轴交于点A,一次函数的图像与x轴交于点B,与交于点C.点P是y轴上一点,点Q是直线上一点.
(1)、求的长;(2)、如果点E为边的中点,联结 , 求的面积;(3)、如图2,延长交射线于点F,联结 , 如果平分 , 求四边形的周长.22. 如图,在平面直角坐标系中,一次函数的图像与x轴交于点A,一次函数的图像与x轴交于点B,与交于点C.点P是y轴上一点,点Q是直线上一点.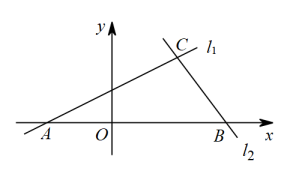 (1)、求的面积;(2)、若点P在y轴的负半轴上,且是轴对称图形,求点P的坐标;(3)、若以P、Q、B、C为顶点的四边形是平行四边形,直接写出点Q的坐标.23. 三角形中位线定理:三角形的中位线平行于第三边,并且等于第三边的一半.如图1,小明在证明这个定理时,通过延长DE到点F,使EF=DE,连接CF,证明△ADE△CFE,再证明四边形DBCF是平行四边形,即可得证.
(1)、求的面积;(2)、若点P在y轴的负半轴上,且是轴对称图形,求点P的坐标;(3)、若以P、Q、B、C为顶点的四边形是平行四边形,直接写出点Q的坐标.23. 三角形中位线定理:三角形的中位线平行于第三边,并且等于第三边的一半.如图1,小明在证明这个定理时,通过延长DE到点F,使EF=DE,连接CF,证明△ADE△CFE,再证明四边形DBCF是平行四边形,即可得证.
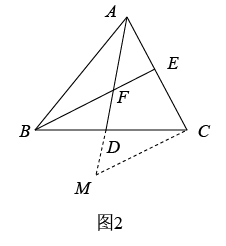

 (1)、【类比迁移】如图2,AD是BC边的中线,BE交AC于点E,交AD于点F,且AC=BF,求证:AE=EF.
(1)、【类比迁移】如图2,AD是BC边的中线,BE交AC于点E,交AD于点F,且AC=BF,求证:AE=EF.小明发现可以类比以上思路进行证明.
证明:如图2,延长AD至点M,使MD=FD,连接MC,……
请你根据小明的思路完成证明过程.
(2)、【方法运用】如图3,在菱形ABCD中,∠D=60°,点E为射线BC上一个动点(在点C右侧),把线段EC绕点E逆时针旋转120°得到线段BC′,连接BC′,点F是BC′的中点,连接AE、CF、EF.①请你判断线段EF和AE的数量关系是 ▲ , 并说明理由;
②若菱形ABCD的边长为6,CF=CE,请直接写出CF的长.
24.(1)、问题提出在平面内,已知线段 , , 则线段的最小值为 .
(2)、问题探究如图1,在平行四边形中, , , , P是边的中点,Q是边上一动点,将三角形沿所在直线翻折,得到三角形 , 连接 , 求的最小值.
(3)、问题解决如图2,平行四边形为某公园平面示意图,扇形为该公园的人口广场,已知 , , , . 为了提升游客体验感,工作人员准备在弧上找一点P , 沿 , 修两条绿色通道,并在上方和右方区域种植花卉供游客观赏,其余地方修建其他设施,求其他设施区域面积的最小值.
 25. 在一次数学研究性学习中,小兵将两个全等的直角三角形纸片ABC和DEF拼在一起,使点A与点F重合,点C与点D重合(如图1),其中∠ACB=∠DFE=90°,BC=EF=3cm,AC=DF=4cm,并进行如下研究活动.
25. 在一次数学研究性学习中,小兵将两个全等的直角三角形纸片ABC和DEF拼在一起,使点A与点F重合,点C与点D重合(如图1),其中∠ACB=∠DFE=90°,BC=EF=3cm,AC=DF=4cm,并进行如下研究活动.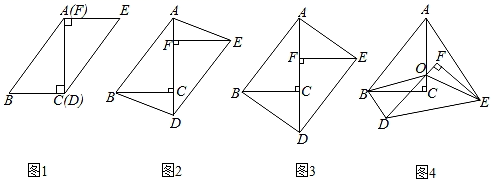 (1)、活动一:将图1中的纸片DEF沿AC方向平移,连结AE,BD(如图2),当点F与点C重合时停止平移.
(1)、活动一:将图1中的纸片DEF沿AC方向平移,连结AE,BD(如图2),当点F与点C重合时停止平移.
(思考)图2中的四边形ABDE是平行四边形吗?请说明理由.(2)、(发现)当纸片DEF平移到某一位置时,小兵发现四边形ABDE为矩形(如图3).求AF的长.(3)、活动二:在图3中,取AD的中点O,再将纸片DEF绕点O顺时针方向旋转α度(0≤α≤90),连结OB,OE(如图4).
(探究)当EF平分∠AEO时,探究OF与BD的数量关系,并说明理由.