【基础卷】北师大版数学八(下)第六章 平行四边形 章末检测
试卷更新日期:2024-05-05 类型:单元试卷
一、选择题(每题3分,共30分)
-
1. 如图,平行四边形ABCD的对角线AC与BD相交于点O, , 若 , , 则BD的长是( )
 A、16 B、18 C、20 D、222. 如图,在平行四边形中,平分 , 则平行四边形的周长是( )
A、16 B、18 C、20 D、222. 如图,在平行四边形中,平分 , 则平行四边形的周长是( ) A、14 B、16 C、18 D、203. 如图,将平行四边形的一边延长至点E,若 , 则( )
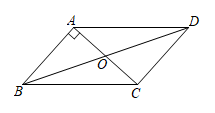
A、14 B、16 C、18 D、203. 如图,将平行四边形的一边延长至点E,若 , 则( )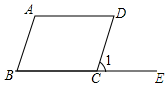 A、115° B、75° C、65° D、55°4. 下列条件中,不能判定四边形为平行四边形的是( )A、 B、 C、 D、5. 下列说法中,错误的是 ( )A、对角线互相平分的四边形是平行四边形 B、两组对边分别相等的四边形是平行四边形 C、一组对边平行且相等的四边形是平行四边形 D、对角线互相垂直且相等的四边形是平行四边形6. 在四边形中, , , 若 , 则的度数为( )A、 B、 C、 D、7. 如图,在△ABC中,D,E,F分别是BC,AC,AB的中点若AB=6,BC=8,则四边形BDEF的周长是( )
A、115° B、75° C、65° D、55°4. 下列条件中,不能判定四边形为平行四边形的是( )A、 B、 C、 D、5. 下列说法中,错误的是 ( )A、对角线互相平分的四边形是平行四边形 B、两组对边分别相等的四边形是平行四边形 C、一组对边平行且相等的四边形是平行四边形 D、对角线互相垂直且相等的四边形是平行四边形6. 在四边形中, , , 若 , 则的度数为( )A、 B、 C、 D、7. 如图,在△ABC中,D,E,F分别是BC,AC,AB的中点若AB=6,BC=8,则四边形BDEF的周长是( ) A、28 B、14 C、10 D、78. 已知一个多边形的外角和比它的内角和少540°,则该多边形的边数是 ( )A、7 B、8 C、9 D、109. 如图,D,E分别是△ABC的边AB,AC的中点.求证:DE∥BC,且.
A、28 B、14 C、10 D、78. 已知一个多边形的外角和比它的内角和少540°,则该多边形的边数是 ( )A、7 B、8 C、9 D、109. 如图,D,E分别是△ABC的边AB,AC的中点.求证:DE∥BC,且.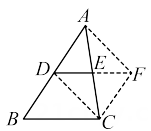
证明:延长 DE 至点 F,使 EF=DE,连结 FC,DC,AF.
又∵AE=EC,
∴四边形ADCF是平行四边形.
以下是接着的排序错误的证明步骤:
①∴DF∥BC.
②∴CF∥AD,即CF∥BD.
③∴四边形 DBCF 是平行四边形.
④∴DE∥BC,且正确的证明顺序应是( )
A、②→③→①→④ B、②→①→③→④ C、①→③→④→② D、①→③→②→④10. 如图,为估计池塘两岸边A , B两点间的距离,在池塘的一侧选取点C , 分别取AC , BC的中点D , E , 测得DE=15m,则A , B两点间的距离是( )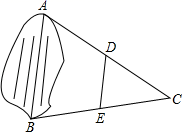 A、15m B、20m C、30m D、60m
A、15m B、20m C、30m D、60m二、填空题(每题3分,共15分)
-
11. 如图,在▱ABCD中,若AB=4,BC=6,AC的垂直平分线交AD于点E,连结CE,则△CDE的周长为.
 12. 如图,在四边形中, , , 若 , 则的大小为(度).
12. 如图,在四边形中, , , 若 , 则的大小为(度). 13. 如图,在▱ABCD中,E,F分别在边 BC,AD 上,有以下条件:①AF=CF;②AE=CF;③∠BEA =∠FCE.若要使四边形AFCE 为平行四边形,则还需添加上述条件中的(填序号).
13. 如图,在▱ABCD中,E,F分别在边 BC,AD 上,有以下条件:①AF=CF;②AE=CF;③∠BEA =∠FCE.若要使四边形AFCE 为平行四边形,则还需添加上述条件中的(填序号).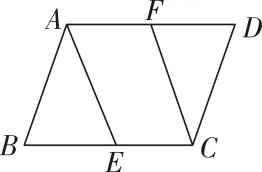 14. 在△ABC中,AB=4,BC=6,AC=8,D,E,F分别为边AB,BC,AC的中点,则△DEF的周长为15. 一个多边形的内角和是其外角和的4倍,则这个多边形的边数是.
14. 在△ABC中,AB=4,BC=6,AC=8,D,E,F分别为边AB,BC,AC的中点,则△DEF的周长为15. 一个多边形的内角和是其外角和的4倍,则这个多边形的边数是.三、解答题(共10题,共75分)
-
16. 如图所示为两张大小完全相同的6×6方格纸,每个小方格都是边长为1的正方形,小方格的顶点叫做格点,以格点为顶点的多边形叫做格点多边形.网格中有一个边长为2的格点正方形,按下列要求画出拼图后的格点平行四边形.
 (1)、把图1中的格点正方形分割成两部分,再通过图形变换拼成一个格点平行四边形,在图1中画出这个格点平行四边形.(2)、把图2中的格点正方形分割成三部分,再通过图形变换拼成一个格点平行四边形,在图2中画出这个格点平行四边形.17. 已知:如图,在▱ABCD中,过 AC的中点O的直线分别交 CB,AD 的延长线于点 E,F.求证:BE=DF.
(1)、把图1中的格点正方形分割成两部分,再通过图形变换拼成一个格点平行四边形,在图1中画出这个格点平行四边形.(2)、把图2中的格点正方形分割成三部分,再通过图形变换拼成一个格点平行四边形,在图2中画出这个格点平行四边形.17. 已知:如图,在▱ABCD中,过 AC的中点O的直线分别交 CB,AD 的延长线于点 E,F.求证:BE=DF. 18. 如图,在中,是它的一条对角线,过两点分别作 , 为垂足.
18. 如图,在中,是它的一条对角线,过两点分别作 , 为垂足.
求证:
(1)、 .(2)、四边形是平行四边形.19. 如图,在中,点D,分别是AC,AB的中点,点是CB延长线上的一点,且CF=3BF,连接DB,EF.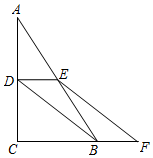 (1)、求证:四边形DEFB是平行四边形;(2)、若 , AC=12 cm,DE=4 cm,求四边形DEFB的周长.20. 已知一个正多边形的边数为n.(1)、若这个多边形的内角和为其外角和的4倍,求n的值.(2)、若这个正多边形的一个内角为 , 求n的值,21. 如图,佳佳从点出发,前进10米后向右转 , 再前进10米后又向右转 , 如此反复下去,直到他第一次回到出发点 , 他所走的路径构成了一个多边形.
(1)、求证:四边形DEFB是平行四边形;(2)、若 , AC=12 cm,DE=4 cm,求四边形DEFB的周长.20. 已知一个正多边形的边数为n.(1)、若这个多边形的内角和为其外角和的4倍,求n的值.(2)、若这个正多边形的一个内角为 , 求n的值,21. 如图,佳佳从点出发,前进10米后向右转 , 再前进10米后又向右转 , 如此反复下去,直到他第一次回到出发点 , 他所走的路径构成了一个多边形. (1)、佳佳一共走了多少米?(2)、求这个多边形的内角和.22. 如图,在中, , , , 点P沿AB边从点A开始以2cm秒的速度向点B移动,同时点Q沿DA边从点D开始以1cm/秒的速度向点A移动,用t表示移动的时间 .
(1)、佳佳一共走了多少米?(2)、求这个多边形的内角和.22. 如图,在中, , , , 点P沿AB边从点A开始以2cm秒的速度向点B移动,同时点Q沿DA边从点D开始以1cm/秒的速度向点A移动,用t表示移动的时间 . (1)、当t为何值时,△PAQ是等边三角形.(2)、当t为何值时,△PAQ为直角三角形.23. 如图,△ABC的中线BE,CF相交于点G,已知P,Q分别是BG,CG的中点.
(1)、当t为何值时,△PAQ是等边三角形.(2)、当t为何值时,△PAQ为直角三角形.23. 如图,△ABC的中线BE,CF相交于点G,已知P,Q分别是BG,CG的中点. (1)、求证:四边形EFPQ是平行四边形;(2)、请判断BG与GE的数量关系,并证明.
(1)、求证:四边形EFPQ是平行四边形;(2)、请判断BG与GE的数量关系,并证明.