【提升卷】2024年北师大版数学八（下）6.4多边形的内角与外角和 同步练习
试卷更新日期：2024-05-05 类型：同步测试
一、选择题
-
1. 若一个多边形的内角和是它的外角和的3倍，则该多边形的边数为（ ）A、6 B、7 C、9 D、82. 一个多边形切去一个角后，形成的另一个多边形的内角和为 ， 原多边形的边数是（ ）A、7或8或9 B、8或9或10 C、6或7或8 D、5或6或73. 一张四边形纸片剪去一个角后，内角和将（ ）A、减少180° B、不变 C、增加180° D、以上都有可能4. 如图，在四边形ABCD中，∠A=∠B=∠C，点E在边AB上，∠AED=60°.设∠ADE=α，∠ADC=β，则一定有（ ）
A、 B、 C、 D、5. 当多边形的边数增加1时，它的内角和会（ ）A、增加90° B、增加180° C、增加270° D、增加360°6. 若把一个多边形割去一个角后，得到的多边形内角和为1440°，则这个多边形原来的边数为（ ）A、9 B、10 C、11 D、以上都有可能7. 如图，五边形ABCDE是正五边形，F，G是边CD，DE上的点，且BF∥AG.若∠CFB=57°，则∠AGD的度数为（ ）
A、114° B、123° C、129° D、135°8. 如图，∠1，∠2，∠3，∠4，∠5是五边形ABCDE的外角，且∠1=∠2=∠3=∠4=67°，则∠AED的度数是（ ）
A、78° B、88° C、92° D、112°9. 如图，小明从点A出发沿直线前进10米到达点B，向左转45%后又沿直线前进10米到达点C，再向左转45°后沿直线前进10米到达点D……照这样走下去，小明第一次回到出发点A时所走的路程为（ ）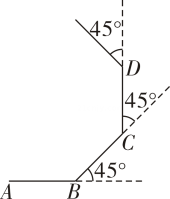
A、100米 B、80米 C、60米 D、40米10. 某科技小组制作了一个机器人，它能根据指令要求进行行走和旋转，某一指令规定：机器人先向前行走2米，然后左转45°，若机器人反复执行这一指令，则从出发到第一次回到原处，机器人共走了（ ）A、14米 B、15米 C、16米 D、17米二、填空题
-
11. 若一个九边形的8个外角的和为200°，则它的第9个外角的度数为°.12. 如果一个多边形的每个外角都等于相邻内角的 ， 则这个多边形的边数为 ．13. 已知一个多边形被截取一个角后，内角和变为 ， 则原多边形的边数为.14. 如图，六边形A₁A₂A₃A₄A₃A₆的内部有一个五边形B₁B₂B₃B₁B₅，六边形的6个内角都相等，五边形的5个内角也都相等，且A₃A₄∥B₃B₄.若直线经过点B₂，B₃，则直线l与A₁A₂的夹角α的度数为°.
15. 如图，蜂巢的横截面由正六边形组成，且能无限无缝隙拼接，称横截面图形由全等正多边形组成，且能无限无缝隙拼接的多边形具有同形结构．若已知具有同形结构的正n边形的每个内角度数为α，满足：360=kα（k为正整数），多边形外角和为360°，则k关于边数n的函数是（写出n的取值范围）
三、作图题
-
16. 如图是一个多边形，你能否用一直线去截这个多边形，使得到的新多边形分别满足下列条件： 画出图形，把截去的部分打上阴影
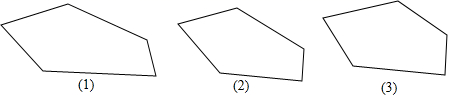(1)、①新多边形内角和比原多边形的内角和增加了 ．②新多边形的内角和与原多边形的内角和相等．
③新多边形的内角和比原多边形的内角和减少了 ．
(2)、将多边形只截去一个角，截后形成的多边形的内角和为 ，求原多边形的边数．四、解答题
-
17. 如图所示，一块较为精密的模板中，AB，CD的延长线应该相交成80°的角，因交点不在模板上，不便测量，测得∠BAE=124°，∠DCF=155°，AE⊥EF，CF⊥EF，此时AB，CD的延长线相交成的角是否符合规定？为什么？
-
