【培优卷】2024年北师大版数学八(下)6.4多边形的内角与外角和 同步练习
试卷更新日期:2024-05-05 类型:同步测试
一、选择题
-
1. 图中表示被撕掉一块的正n边形纸片,若(即延长a和b相交形成垂直),则n的值是( )
 A、6 B、8 C、10 D、122. 如图, , , 若 , 则的度数为( )
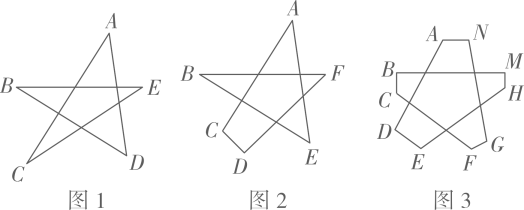
A、6 B、8 C、10 D、122. 如图, , , 若 , 则的度数为( ) A、90° B、60° C、70° D、80°3. 如图,∠A+∠B+∠C+∠D+∠E+∠F的度数为( )
A、90° B、60° C、70° D、80°3. 如图,∠A+∠B+∠C+∠D+∠E+∠F的度数为( ) A、180° B、360° C、270° D、540°4. 如图,、、 , 是六边形的四个外角,延长交于点若 , 则的度数为( )
A、180° B、360° C、270° D、540°4. 如图,、、 , 是六边形的四个外角,延长交于点若 , 则的度数为( ) A、 B、 C、 D、5. 已知n边形的每个内角都相等,则使得n边形的每个内角的度数都是整数的n的值有( )A、18个 B、20个 C、22个 D、无数个6. 一副三角尺如图所示摆放,则与的数量关系为( )
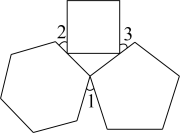
A、 B、 C、 D、5. 已知n边形的每个内角都相等,则使得n边形的每个内角的度数都是整数的n的值有( )A、18个 B、20个 C、22个 D、无数个6. 一副三角尺如图所示摆放,则与的数量关系为( )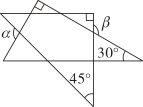 A、 B、 C、 D、7. 将一长方形纸片沿一条直线剪成两个多边形,那么这两个多边形的内角和之和不可能是( )A、360° B、540° C、720° D、730°8. 如图,在边长为1的正六边形 中,M是边 上一点,则线段 的长可以是( )
A、 B、 C、 D、7. 将一长方形纸片沿一条直线剪成两个多边形,那么这两个多边形的内角和之和不可能是( )A、360° B、540° C、720° D、730°8. 如图,在边长为1的正六边形 中,M是边 上一点,则线段 的长可以是( ) A、1.4 B、1.6 C、1.8 D、2.2
A、1.4 B、1.6 C、1.8 D、2.2二、填空题
-
9. 如图由内角分别相等的四边形、五边形、六边形组合而成的图形中, , 则的度数为度.
 10. 如图,∠A+∠B+∠C+∠D+∠E+∠F+∠G的度数为 .
10. 如图,∠A+∠B+∠C+∠D+∠E+∠F+∠G的度数为 . 11. 如图, , E、F分别是AB、CD上的点,EH、FH分别是∠AEG和∠CFG的角平分线.若∠G=110°,则∠H=°.
11. 如图, , E、F分别是AB、CD上的点,EH、FH分别是∠AEG和∠CFG的角平分线.若∠G=110°,则∠H=°. 12. 如图,正n边形A1A2A3……An(每条边相等,每个内角都相等)竖立于地面,一边与地面重合,一束太阳光平行照射在正n边形上,若∠1-∠2=36°,则n= .
12. 如图,正n边形A1A2A3……An(每条边相等,每个内角都相等)竖立于地面,一边与地面重合,一束太阳光平行照射在正n边形上,若∠1-∠2=36°,则n= .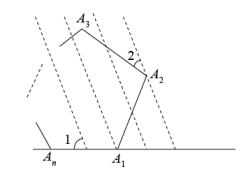
三、解答题
-
13. 如果一个多边形的各边都相等,且各内角也都相等,那么这个多边形就叫做正多边形,下图是一组正多边形,观察每个正多边形中∠α的变化情况,解答下列问题.
 (1)、将下面的表格补充完整:
(1)、将下面的表格补充完整:正多边形的边数
3
4
5
6
……
n
∠α的度数
60°
……
(2)、根据规律,是否存在一个正n边形,使其中的∠α=16°?若存在,直接写出n的值;若不存在,请说明理由.14. 已知:如图,边形. (1)、求证:边形的内角和等于;(2)、在一个各内角都相等的多边形中,每一个内角都比相邻的外角的3倍还大20°,求这个多边形的内角和;(3)、粗心的小明在计算一个多边形的内角和时,误把一个外角也加进去了,得其和为1180°,这个多加的外角度数为 ,多边形的边数为 .
(1)、求证:边形的内角和等于;(2)、在一个各内角都相等的多边形中,每一个内角都比相邻的外角的3倍还大20°,求这个多边形的内角和;(3)、粗心的小明在计算一个多边形的内角和时,误把一个外角也加进去了,得其和为1180°,这个多加的外角度数为 ,多边形的边数为 .