【提升卷】2024年北师大版数学八(下)6.3三角形的中位线 同步练习
试卷更新日期:2024-05-05 类型:同步测试
一、选择题
-
1. 如图,M 是△ABC的边 BC 的中点,AN平分∠BAC,BN⊥AN,且 AB=10,MN=3,则AC的长( )
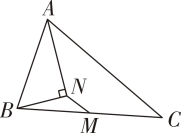 A、12 B、14 C、16 D、182. 如图,□ABCD的周长为 36,对角线 AC,BD 相交于点O,E 是CD 的中点,连结OE.若 BD =12,则△DOE 的周长为 ( )
A、12 B、14 C、16 D、182. 如图,□ABCD的周长为 36,对角线 AC,BD 相交于点O,E 是CD 的中点,连结OE.若 BD =12,则△DOE 的周长为 ( ) A、15 B、18 C、21 D、243. 如图,在△ABC中,∠C=90°,E是CA延长线上-点,F是CB上一点,AE=12,BF=8,点P,Q,D分别是AF ,BE,AB的中点,则PQ的长为( )
A、15 B、18 C、21 D、243. 如图,在△ABC中,∠C=90°,E是CA延长线上-点,F是CB上一点,AE=12,BF=8,点P,Q,D分别是AF ,BE,AB的中点,则PQ的长为( )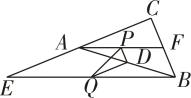 A、 B、4 C、6 D、4. 如图,ABCD的对角线AC,BD相交于点O,∠ADC的平分线与边AB相交于点P,E是PD中点,若AD=4,CD=6,则EO的长为( )
A、 B、4 C、6 D、4. 如图,ABCD的对角线AC,BD相交于点O,∠ADC的平分线与边AB相交于点P,E是PD中点,若AD=4,CD=6,则EO的长为( ) A、1 B、2 C、3 D、45. 如图,在平行四边形中, , , , , 分别是边 , 上的动点,连接 , , , 分别是 , 的中点,连接 , 则的最大值与最小值的差为( )
A、1 B、2 C、3 D、45. 如图,在平行四边形中, , , , , 分别是边 , 上的动点,连接 , , , 分别是 , 的中点,连接 , 则的最大值与最小值的差为( )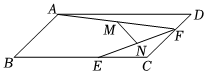 A、 B、 C、 D、6. 如图,点D,E分别是的边上的中点,的角平分线交于点F, , 则的长为( )
A、 B、 C、 D、6. 如图,点D,E分别是的边上的中点,的角平分线交于点F, , 则的长为( ) A、1 B、1.5 C、2 D、2.57. 如图,△ABC的中线BD、CE交于点O,连接OA,点G,F分别为OC,OB的中点,BC=4,AO=3,则四边形DEFG的周长为( )
A、1 B、1.5 C、2 D、2.57. 如图,△ABC的中线BD、CE交于点O,连接OA,点G,F分别为OC,OB的中点,BC=4,AO=3,则四边形DEFG的周长为( )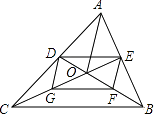 A、6 B、7 C、8 D、128. 如图,直线y=x+4与x轴、y轴分别交于点A和点B,点C,D分别为线段AB,OB的中点,点P为OA边上的一个动点,当PC+PD值最小时,点P的坐标为( )
A、6 B、7 C、8 D、128. 如图,直线y=x+4与x轴、y轴分别交于点A和点B,点C,D分别为线段AB,OB的中点,点P为OA边上的一个动点,当PC+PD值最小时,点P的坐标为( )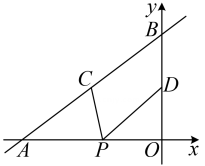 A、 B、(-6,0) C、 D、
A、 B、(-6,0) C、 D、二、填空题
-
9. 如图,EF是△ABC的中位线,BD平分∠ABC交EF于点D , 若AE=3,DF=1,则边BC的长为 .
 10. 如图,四边形ABCD中,∠A=90°,AB=2 ,AD=2,点M,N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF长度的最大值为 .
10. 如图,四边形ABCD中,∠A=90°,AB=2 ,AD=2,点M,N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF长度的最大值为 . 11. 如图,中, , 为边上的中点,为边上一点, , 连接、 , 延长交延长线于 , 若 , , 则 .
11. 如图,中, , 为边上的中点,为边上一点, , 连接、 , 延长交延长线于 , 若 , , 则 . 12. 如图,D,E分别是△ABC的边AB,AC的中点,连结DE,BE,过点C作CF∥BE,交 DE的延长线于点F.若EF=3,则DE的长为.
12. 如图,D,E分别是△ABC的边AB,AC的中点,连结DE,BE,过点C作CF∥BE,交 DE的延长线于点F.若EF=3,则DE的长为. 13. 如图,△ABC的周长为 28,点 D,E都在边BC 上,∠ABC 的平分线垂直于 AE,垂足为 Q,∠ACB的平分线垂直于 AD,垂足为 P,连结PQ.若 BC=10,则PQ的长是.
13. 如图,△ABC的周长为 28,点 D,E都在边BC 上,∠ABC 的平分线垂直于 AE,垂足为 Q,∠ACB的平分线垂直于 AD,垂足为 P,连结PQ.若 BC=10,则PQ的长是.
三、综合题
-
14. 如图,在四边形ABCD中,AC=BD , AC、BD交于点O , E、F分别是AB、CD中点,EF分别交AC、BD于点H、G . 求证:OG=OH .
 15. 在中, , E、F分别是、的中点,延长到点D,使 , 连接、、 , 与交于点O.
15. 在中, , E、F分别是、的中点,延长到点D,使 , 连接、、 , 与交于点O. (1)、试说明与互相平分;(2)、若 , , 求的长.16. 如图,在平行四边形中,E,F分别是 , 边上的点, , 连接和的交点为M,和的交点为N,连接 , .
(1)、试说明与互相平分;(2)、若 , , 求的长.16. 如图,在平行四边形中,E,F分别是 , 边上的点, , 连接和的交点为M,和的交点为N,连接 , . (1)、求证:四边形为平行四边形.(2)、若 , 求的长.17. 阅读与思考
(1)、求证:四边形为平行四边形.(2)、若 , 求的长.17. 阅读与思考请阅读下列材料,并完成相应的任务.
年月日星期一
今天,同学们学习了三角形中位线定理的相关内容,知道了“三角形的中位线平行于第三边,且等于第三边的一半”.课下,对三角形中位线定理的相关知识进行了复习,并对它相关的命题产生了兴趣.如图1,在中,分别是边上的点,同学们提出了以下三个命题:
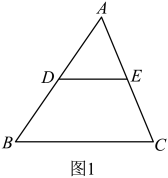
I.若是边的中点,且 , 则是边的中点.
II.若 , 且 , 则分别是边的中点.
III.若是边的中点,且 , 则是边的中点.
任务:
(1)、从所提出的三个命题中选择一个假命题,并在图2中画出反例.(要求:尺规作图,保留作图痕迹) (2)、从所提出的三个命题中选择一个真命题进行证明.
(2)、从所提出的三个命题中选择一个真命题进行证明.