【培优卷】2024年北师大版数学八(下)6.3三角形的中位线 同步练习
试卷更新日期:2024-05-05 类型:同步测试
一、选择题
-
1. 如图,在△ABC中,D,E分别是边 AB,BC的中点,点F 在射线DE 上.添加一个条件,使得四边形ADFC为平行四边形,则这个条件可以是( )
 A、∠B=∠F B、DE=EF C、AC=CF D、AD=CF2. 如图,在正方形中,点E , F分别是 , 的中点, , 相交于点M , G为上一点,N为的中点.若 , , 则线段的长度为( )
A、∠B=∠F B、DE=EF C、AC=CF D、AD=CF2. 如图,在正方形中,点E , F分别是 , 的中点, , 相交于点M , G为上一点,N为的中点.若 , , 则线段的长度为( )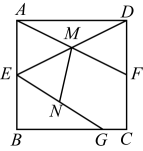 A、 B、 C、2 D、3. 我们知道:五边形具有不稳定性,小文将正五边形沿箭头方向向右推,使点B在线段AC上,若 , 则( )
A、 B、 C、2 D、3. 我们知道:五边形具有不稳定性,小文将正五边形沿箭头方向向右推,使点B在线段AC上,若 , 则( ) A、减小了 B、增加了 C、减少了 D、增加了4. 如图,是锐角三角形,是的中点,分别以 , 为边向外侧作等腰三角形和等腰三角形 . 点 , 分别是底边 , 的中点,连接 , , 若(是锐角),则的度数是( )
A、减小了 B、增加了 C、减少了 D、增加了4. 如图,是锐角三角形,是的中点,分别以 , 为边向外侧作等腰三角形和等腰三角形 . 点 , 分别是底边 , 的中点,连接 , , 若(是锐角),则的度数是( ) A、 B、 C、 D、5. 如图,在Rt△ABC中,∠C=90°,AC=4,AB=8,点D是AC上一个动点,以AB为对角线的所有平行四边形ADBE中,线段DE的最小值是( )
A、 B、 C、 D、5. 如图,在Rt△ABC中,∠C=90°,AC=4,AB=8,点D是AC上一个动点,以AB为对角线的所有平行四边形ADBE中,线段DE的最小值是( ) A、4 B、 C、 D、66. 如图,在 中, , , 分别是 , 的中点, , 为 上的点,连接 , .若 cm, cm, cm,则图中阴影部分面积为( )
A、4 B、 C、 D、66. 如图,在 中, , , 分别是 , 的中点, , 为 上的点,连接 , .若 cm, cm, cm,则图中阴影部分面积为( )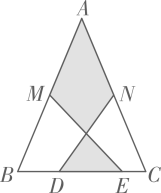 A、25cm2 B、35cm2 C、30cm2 D、42cm27. 如图,在中, , 于点 , 于点 , 于点 , , 则( )
A、25cm2 B、35cm2 C、30cm2 D、42cm27. 如图,在中, , 于点 , 于点 , 于点 , , 则( ) A、 B、 C、 D、8. 在▱ABCD中,对角线AC、BD相交于点O,BD=2AD,E、F、G分别是OC、OD、AB的中点,下列结论:①GN=NE;②AE⊥GF;③AC平分∠BCD;④AC⊥BD,其中正确的个数是( )
A、 B、 C、 D、8. 在▱ABCD中,对角线AC、BD相交于点O,BD=2AD,E、F、G分别是OC、OD、AB的中点,下列结论:①GN=NE;②AE⊥GF;③AC平分∠BCD;④AC⊥BD,其中正确的个数是( ) A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
9. 如图,等腰直角中, , , 为中点.点为射线上的一个动点,以为直角边向右上方构造等腰直角 , , 连接 . 在点的运动过程中,长度的最小值是 .
 10. 如图,在平行四边形中,对角线、交于点 , 将沿着对角线翻折得到 , 连接 . 若 , , , 则到的距离为 .
10. 如图,在平行四边形中,对角线、交于点 , 将沿着对角线翻折得到 , 连接 . 若 , , , 则到的距离为 . 11. 如图,▱ABCD中∠D=75°,AB=4,AC=BC,点E为线段AD上一动点,过点E作EF⊥AC于点F,连接BE,点G为BE中点,连接GF.当GF最小时,线段AF的值为 .
11. 如图,▱ABCD中∠D=75°,AB=4,AC=BC,点E为线段AD上一动点,过点E作EF⊥AC于点F,连接BE,点G为BE中点,连接GF.当GF最小时,线段AF的值为 . 12. 如图,的三边长分别为 , , , 以它的三边中点为顶点组成一个新三角形,以这个新三角形三边中点为顶点又组成一个小三角形, , 以此类推,第次组成的三角形的周长 .
12. 如图,的三边长分别为 , , , 以它的三边中点为顶点组成一个新三角形,以这个新三角形三边中点为顶点又组成一个小三角形, , 以此类推,第次组成的三角形的周长 . 13. 如图1是雨伞的结构示意图.OP是伞柄,OM,AB,CD是伞骨.已知点A,C分别是OM,AB的中点.CD=(dm),点B,D在OP上滑动时,可将雨伞打开或收拢.当OP与水平面垂直时打开雨伞,雨伞能罩住的水平面大小可近似地看成一个圆.如图2,当雨伞完全打开时,∠ABD=90°;再将雨伞收拢到如图3,此时B′D′=1(dm),且点C′到OP的距离恰好等于图2中BD的长.则伞骨AB的长为 (dm),设图2中能罩住的水平面面积是S1 , 图3中能罩住的水平面面积是S2 , 则= .
13. 如图1是雨伞的结构示意图.OP是伞柄,OM,AB,CD是伞骨.已知点A,C分别是OM,AB的中点.CD=(dm),点B,D在OP上滑动时,可将雨伞打开或收拢.当OP与水平面垂直时打开雨伞,雨伞能罩住的水平面大小可近似地看成一个圆.如图2,当雨伞完全打开时,∠ABD=90°;再将雨伞收拢到如图3,此时B′D′=1(dm),且点C′到OP的距离恰好等于图2中BD的长.则伞骨AB的长为 (dm),设图2中能罩住的水平面面积是S1 , 图3中能罩住的水平面面积是S2 , 则= .
三、解答题
-
14. 已知,是的中线,过点C作 .
 (1)、如图1,交于点F,连接 . 求证:四边形是平行四边形;(2)、P是线段上一点(不与点A,D重合),交于点F,交于点E,连接 .
(1)、如图1,交于点F,连接 . 求证:四边形是平行四边形;(2)、P是线段上一点(不与点A,D重合),交于点F,交于点E,连接 .①如图2,四边形是平行四边形吗?请说明理由.
②如图3,延长交于点Q,若 , , ,请直接写出的值.
15. 下面是证明三角形中位线定理的两种添加辅助线的方法,选择其中一种,完成证明.三角形中位线定理:三角形的中位线平行于第三边,并且等于第三边的一半.
已知:如图,在中,点D , E分别是 , 边的中点.求证: , 且 .
 (1)、方法一:证明:如图,延长到点 , 使 , 连接 , , .
(1)、方法一:证明:如图,延长到点 , 使 , 连接 , , .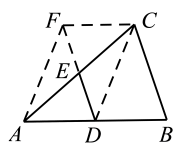 (2)、方法二:证明:如图,取中点 , 连接并延长到点 , 使 , 连接 .
(2)、方法二:证明:如图,取中点 , 连接并延长到点 , 使 , 连接 . 16.
16. (1)、课本再现
(1)、课本再现已知:如图,是的中位线.求证: , 且 .
定理证明
证明:如图1,延长至点 , 使得 , 连接 . 请你根据小乐添加的辅助线,写出完整的证明过程;(不再添加新的辅助线)
(2)、知识应用如图2,在四边形中, , , , , 点 , , 分别是 , , 的中点,求的长.
17.(1)、回归课本请用文字语言表述三角形的中位线定理: .
(2)、回顾证法证明三角形中位线定理的方法很多,但多数都要通过添加辅助线构图完成.下面是其中一种辅助线的添加方法.请结合图2,补全求证及证明过程.
已知:在中,点D , E分别是的中点.
求证:_▲_.
证明:过点作 , 与的延长线交于点 .
(3)、实践应用如图3,点和点被池塘隔开,在外选一点 , 连接 , 分别取的中点D , E , 测得的长度为9米,则B , C两点间的距离为 .
