【培优卷】2024年北师大版数学八(下)6.2平行四边形的判定 同步练习
试卷更新日期:2024-05-05 类型:同步测试
一、选择题
-
1. 如图,在▱ABCD中,对角线AC,BD相交于点O,AE⊥BD于点E,CF⊥BD于点F,连结AF,CE,有下列结论:①CF=AE;②OE=OF;③DE=BF;④图中共有10对全等三角形.其中正确的是( )
 A、③④ B、①②③ C、①②④ D、①②③④2. 如图,在平行四边形ABCD中,AB=5,BC=8,∠ABC和∠BCD的角平分线分别交AD于点E和F,若BE=6,则CF=( )
A、③④ B、①②③ C、①②④ D、①②③④2. 如图,在平行四边形ABCD中,AB=5,BC=8,∠ABC和∠BCD的角平分线分别交AD于点E和F,若BE=6,则CF=( ) A、6 B、8 C、10 D、133. 如图,已知点D是等边三角形ABC中BC的中点,BC=2,点E是AC边上的动点,则BE+ED的和最小值为( )
A、6 B、8 C、10 D、133. 如图,已知点D是等边三角形ABC中BC的中点,BC=2,点E是AC边上的动点,则BE+ED的和最小值为( )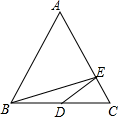 A、 B、 C、3 D、4. 现有一张平行四边形纸片, , 要求用尺规作图的方法在边 , 上分别找点 , 使得四边形为平行四边形,甲、乙两位同学的作法如图所示,下列判断正确的是( )
A、 B、 C、3 D、4. 现有一张平行四边形纸片, , 要求用尺规作图的方法在边 , 上分别找点 , 使得四边形为平行四边形,甲、乙两位同学的作法如图所示,下列判断正确的是( ) A、甲对、乙不对 B、甲不对、乙对 C、甲、乙都对 D、甲、乙都不对5. 如图,是的边上的点,是中点,连接并延长交于点 , 连接与相交于点 , 若 , , 则阴影部分的面积为( )
A、甲对、乙不对 B、甲不对、乙对 C、甲、乙都对 D、甲、乙都不对5. 如图,是的边上的点,是中点,连接并延长交于点 , 连接与相交于点 , 若 , , 则阴影部分的面积为( ) A、24 B、17 C、13 D、106. 如图,已知▱OABC的顶点A,C分别在直线 和 上,O是坐标原点,则对角线OB长的最小值为( )
A、24 B、17 C、13 D、106. 如图,已知▱OABC的顶点A,C分别在直线 和 上,O是坐标原点,则对角线OB长的最小值为( )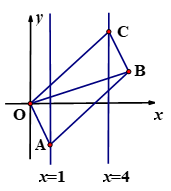 A、3 B、4 C、5 D、67. 如图,在△ABC中, , , , △ABD , △ACE , △BCF都是等边三角形,下列结论中:①;②四边形AEFD是平行四边形;③;④ . 正确的个数是( )
A、3 B、4 C、5 D、67. 如图,在△ABC中, , , , △ABD , △ACE , △BCF都是等边三角形,下列结论中:①;②四边形AEFD是平行四边形;③;④ . 正确的个数是( ) A、1个 B、2个 C、3个 D、4个8. 如图,在▱中,点 , 是对角线上的两个点,且 , 连接 , 求证: .
A、1个 B、2个 C、3个 D、4个8. 如图,在▱中,点 , 是对角线上的两个点,且 , 连接 , 求证: .
证法:如图,在▱中, , ,
.
又 ,
≌ ,
,
,
即 , .

证法:如图,连接交于点 , 连接 , .
在▱中, , .
又 ,
, 即 .
四边形是平行四边形,
.

下列说法错误的是( )
A、证法中证明三角形全等的直接依据是 B、证法中用到了平行四边形的对角线互相平分 C、证法和证法都用到了平行四边形的判定 D、证法和证法都用到了平行四边形的性质二、填空题
-
9. 如图,中, , 若D , E是边上的两个动点,F是边上的一个动点, , 则的最小值为 .
 10. 如图,在菱形中,线段在对角线上运动, , , , 则周长的最小值为 .
10. 如图,在菱形中,线段在对角线上运动, , , , 则周长的最小值为 .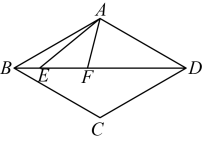 11. 如图,在中,点E , F分别是 , 边的中点,延长至点 , 使 , 以 , 为边向外构造 , 连接交于点 , 连接 . 若 , , 则的长为 .
11. 如图,在中,点E , F分别是 , 边的中点,延长至点 , 使 , 以 , 为边向外构造 , 连接交于点 , 连接 . 若 , , 则的长为 .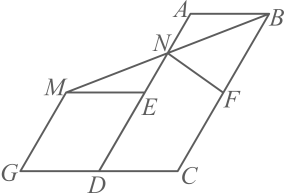 12. 在四边形中,现给出下列结论:
12. 在四边形中,现给出下列结论:①若 , , 则四边形是平行四边形;②若 , , 则四边形是平行四边形;③若 , , 则四边形是平行四边形;④ , , 则四边形是平行四边形.
其中正确的结论是 . (写出所有正确结论的序号)
三、实践探究题
-
13. 如图,在平行四边形ABCD中,AD=2AB=6cm,BE是∠ABC的角平分线,点M从点E出发,沿ED方向以1cm/s的速度向点D运动,点N从点C出发,沿射线CB方向以4cm/s的速度运动,当点M运动到点D时,点N随之停止运动,设运动时间为t(s),
 (1)、求AE的长;(2)、是否存在以M、E、B、N为顶点的四边形是平行四边形?若存在,求出t的值;若不存在,请说明理由.(3)、当时,线段NM将平行四边形ABCD面积二等分(直接写出答案)”14. 如图,△ABC是等边三角形,点D是边BC上的一点,以AD为边作等边△ADE,过点C作CF∥DE交AB于点F.
(1)、求AE的长;(2)、是否存在以M、E、B、N为顶点的四边形是平行四边形?若存在,求出t的值;若不存在,请说明理由.(3)、当时,线段NM将平行四边形ABCD面积二等分(直接写出答案)”14. 如图,△ABC是等边三角形,点D是边BC上的一点,以AD为边作等边△ADE,过点C作CF∥DE交AB于点F. (1)、若点D是BC边的中点(如图①) ,求证:EF=CD.(2)、在(1)的条件下直接写出△AEF和△ABC的面积比.(3)、若点D是BC边上的任意一点(除B,C外,如图②) ,那么(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.15. 在□ABCD中,点O是对角线BD的中点,点E在边BC上,EO的延长线与边AD交于点F , 连接BF、DE如图1.
(1)、若点D是BC边的中点(如图①) ,求证:EF=CD.(2)、在(1)的条件下直接写出△AEF和△ABC的面积比.(3)、若点D是BC边上的任意一点(除B,C外,如图②) ,那么(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.15. 在□ABCD中,点O是对角线BD的中点,点E在边BC上,EO的延长线与边AD交于点F , 连接BF、DE如图1. (1)、求证:四边形BEDF是平行四边形;(2)、若DE=DC , ∠CBD=45°,过点C作DE的垂线,与DE、BD、BF分别交于点G、H、P如图2.
(1)、求证:四边形BEDF是平行四边形;(2)、若DE=DC , ∠CBD=45°,过点C作DE的垂线,与DE、BD、BF分别交于点G、H、P如图2.①当CD=6.CE=4时,求BE的长;
②求证:CD=CH .
16. 如图1,在平行四边形中,的平分线交于点E,的平分线交于点F. (1)、试探究四边形的形状,并说明理由;(2)、如图2,连接 , 若 , 求的长;(3)、如图3,连接 , 将沿直线翻折得到 , 其中点A、B的对应点分别为点C、G,恰好有 , 垂足为点N,交于点M.
(1)、试探究四边形的形状,并说明理由;(2)、如图2,连接 , 若 , 求的长;(3)、如图3,连接 , 将沿直线翻折得到 , 其中点A、B的对应点分别为点C、G,恰好有 , 垂足为点N,交于点M.①试探究的形状,并说明理由;
②若 , 求的长.
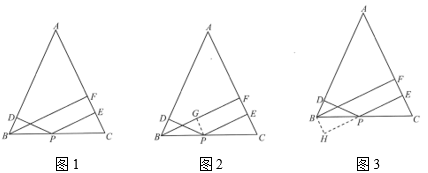
17. 【问题背景】某“数学学习兴趣小组”在学习了“等腰三角形的性质”和“平行四边形的性质和判定”后,在习题中发现了这样一个问题:如图1,在等腰中, , 点D、E分别是边上的点,点P是底边上的点,且 , 过点B作于点F,请写出线段、、之间满足的数量关系式.
同学们经过交流讨论,得到了如下两种解决思路:
解决思路1:如图2,过点P作于点G;
解决思路2:如图3,过点B作 , 交的延长线于点H;
 (1)、上述两种解决思路都可以证明一组三角形全等,判定一个四边形为平行四边形,从而可证得线段之间满足的数量关系式为 .(2)、【类比探究】
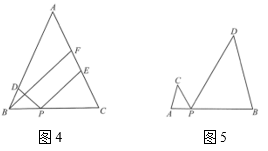
(1)、上述两种解决思路都可以证明一组三角形全等,判定一个四边形为平行四边形,从而可证得线段之间满足的数量关系式为 .(2)、【类比探究】如图4,在等腰中, , 点D、E分别是边上的点,点P是底边上的点,且 , 过点B作交于点F,请写出线段之间满足的数量关系式,并说明理由.
(3)、 【拓展应用】如图5,在与中, , , 点A、B、P在同一条直线上,若 , , 则 .