【提升卷】2024年北师大版数学八（下）6.1平行四边形 同步练习
试卷更新日期：2024-05-05 类型：同步测试
一、选择题
-
1. 如图，EF过平行四边形ABCD对角线的交点O，交AD于点E，交BC于点F，若平行四边形ABCD的周长是30，OE=3，则四边形ABFE的周长是（ ）
A、21 B、24 C、27 D、182. 如图，▱ABCD的周长为 30cm，△ABC 的周长为27cm，则AO的长为 （ ）
A、12cm B、9cm C、7. 5cm D、6cm3. 如果平行四边形的一边长为12，那么这个平行四边形的两条对角线的长可以是 （ ）A、8 和14 B、10 和14 C、18 和20 D、10 和344. 如图，在□ABCD中，E，F是对角线BD上的两点.若添加一个条件，使△ABE≌△CDF，则添加的条件不能为（ ）
A、BE=DF B、BF=DE C、AE=CF D、∠1=∠25. 如图，在中，将沿AC折叠后，点D恰好落在DC的延长线上的点E处．若 ， 则的周长为（ ）
A、24 B、22 C、16 D、126. 如图，在平行四边形ABCD中，∠ABC的平分线交AD于点E，过点A作AF⊥BE，垂足为点F，若AF＝5，BE＝24，则CD的长为（ ）
A、8 B、13 C、16 D、187. 如图，在平行四边形中，平分线交于点 ， 的平分线交于点 ， 若 ， ， 则的长（ ）
A、 B、 C、 D、8. 如图，在中，对角线、交于点O．若 ， ， ， ． 则化简：的结果为（ ）
A、 B、 C、 D、二、填空题
-
9. 如图，平行四边形的对角线相交于点 ， 且 ， 的周长为22，则平行四边形的两条对角线的和是.
10. 如图，在平行四边形中， ， 的平分线交于点E，交的延长线于点F，则cm．
11. 如图，▱ABCD 的顶点C 在等边三角形BEF 的边BF 上，点A在EB 的延长线上，G为DE 的中点，连结CG.若AD=3，AB=CF=2，则CG 的长为.
12. 如图，在▱ABCD中，BC=2AB，E 为BC的中点，则∠AED= °.
三、解答题
-
13. 如图，AC是▱ABCD的对角线，∠BAC=∠DAC．
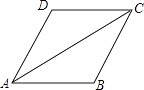(1)、求证：AB=BC；(2)、若AB=2，AC=2 ，求▱ABCD的面积．14. 如图，在平行四边形中，已知 ．
(1)、尺规作图：延长 ， 并在延长线上截取 ， 连接交于点E；（保留作图痕迹，不写作法）(2)、若 ， 求平行四边形的周长．15. 如图，在平行四边形ABCD中，对角线AC ， BD交于点O ， 过点O作直线EF⊥AB ， 分别交AB ， CD于点E ， F ．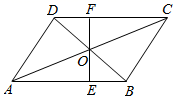
(1)、求证：OE＝OF；(2)、若AC＝18，EF＝10，求AE的长．16. 如图，在四边形ABCD中，AC⊥BD于点E，AB=AC=BD，M为BC的中点，N为线段AM上的点，且MB=MN.
(1)、求证：BN平分∠ABE.(2)、连结DN，若BD=1，四边形DNBC为平行四边形，求线段BC的长.17. 在□ABCD 中，∠ABC = 45°，对角 线 AC ⊥CD.
(1)、如图1，若 AD=6，求□ABCD的面积.(2)、如图2，连结 BD交 AC 于点O，过点 A 作AE⊥BD于点 E，连结 EC.求证：ED=AE+EC.18. 如图①，在平行四边形ABCD中， AB=3，AD=6．动点P沿AD边以每秒个单位长度的速度从点A向终点D ．设点P运动的时间为t（t＞0）秒．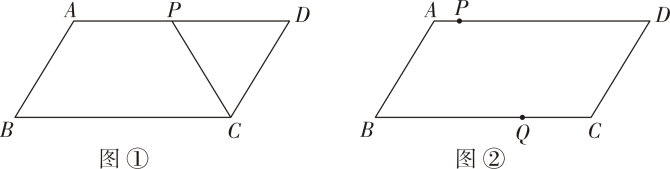
(1)、线段PD的长为 （用含t的代数式表示）．(2)、当CP平分∠BCD时，求t的值．(3)、如图②，另一动点Q以每秒2个单位长度的速度从点C出发，在CB上往返运动．P、Q两点同时出发，点Q也随之停止运动．当以P、D、Q、B为顶点的四边形是平行四边形时，直接写出t的值．