【培优卷】2024年北师大版数学八(下)6.1平行四边形 同步练习
试卷更新日期:2024-05-05 类型:同步测试
一、选择题
-
1. 如图,平行四边形中, , , 平分 , 交于E , 交于点 , 交于点 , 作交于点 , 则( )
 A、 B、 C、1 D、2. 如图,在平面直角坐标系中,▱OABC的顶点A,C分别在直线x=1和x=4上,O是坐标原点,则对角线OB长的最小值为( )
A、 B、 C、1 D、2. 如图,在平面直角坐标系中,▱OABC的顶点A,C分别在直线x=1和x=4上,O是坐标原点,则对角线OB长的最小值为( )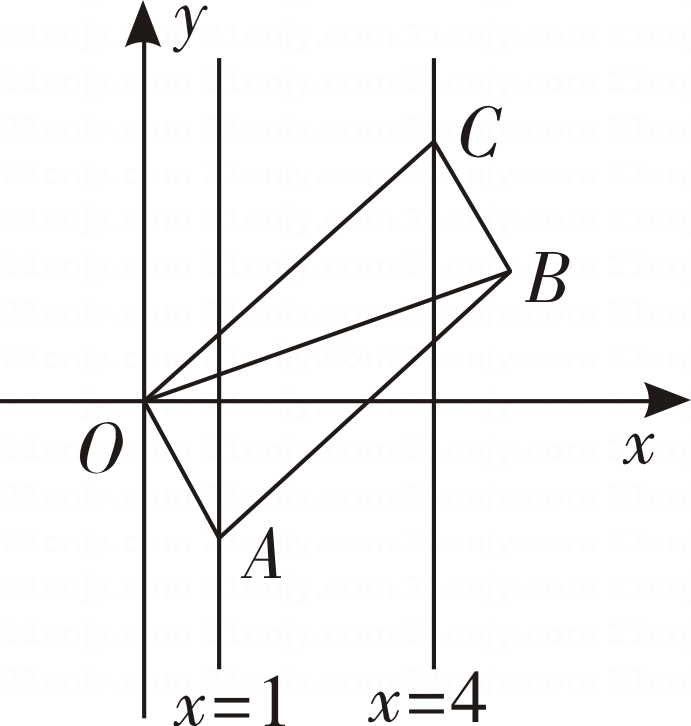 A、3 B、4 C、5 D、63. 如图,平行四边形ABCD中,AE平分∠BAD,交BC于点E,且AB=AE,延长AB与DE的延长线交于点F,连接AC、CF. 下列结论:①△ABC≌△EAD;②△ABE是等边三角形;③AD=AF;④S△BEF=S△ABE . 其中正确的有( )
A、3 B、4 C、5 D、63. 如图,平行四边形ABCD中,AE平分∠BAD,交BC于点E,且AB=AE,延长AB与DE的延长线交于点F,连接AC、CF. 下列结论:①△ABC≌△EAD;②△ABE是等边三角形;③AD=AF;④S△BEF=S△ABE . 其中正确的有( )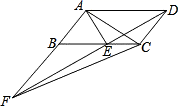 A、1个 B、2个 C、3个 D、4个4. 如图,在平面直角坐标系中,四边形OABC是平行四边形,且顶点的坐标为 , 点的坐标为 , 将平行四边形OABC沿着直线OC翻折,得到四边形 , 若直线把六边形的面积分成相等的两部分,则直线的解析式为( )
A、1个 B、2个 C、3个 D、4个4. 如图,在平面直角坐标系中,四边形OABC是平行四边形,且顶点的坐标为 , 点的坐标为 , 将平行四边形OABC沿着直线OC翻折,得到四边形 , 若直线把六边形的面积分成相等的两部分,则直线的解析式为( ) A、或 B、或 C、或 D、或5. 如图,在▱ABCD , O是AC、BD的交点,过点O与AC垂直的直线交边AD于点E , 若△CDE的周长为11cm , 则平行四边形ABCD的周长为( )
A、或 B、或 C、或 D、或5. 如图,在▱ABCD , O是AC、BD的交点,过点O与AC垂直的直线交边AD于点E , 若△CDE的周长为11cm , 则平行四边形ABCD的周长为( ) A、20cm B、22cm C、24cm D、26cm6. 如图,在▱ABCD中,BE⊥CD,BF⊥AD,∠EBF=45°.若CE=3,DF=1,则▱ABCD的面积为( )
A、20cm B、22cm C、24cm D、26cm6. 如图,在▱ABCD中,BE⊥CD,BF⊥AD,∠EBF=45°.若CE=3,DF=1,则▱ABCD的面积为( )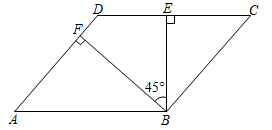 A、 B、 C、 D、7. 如图,在平行四边形中,对角线 , 分别以点为圆心,以大于的长为半径画弧,两弧相交于点和点 , 作直线 , 交对角线于点 , 连接恰好垂直于边 , 若 , 则的长是( )
A、 B、 C、 D、7. 如图,在平行四边形中,对角线 , 分别以点为圆心,以大于的长为半径画弧,两弧相交于点和点 , 作直线 , 交对角线于点 , 连接恰好垂直于边 , 若 , 则的长是( )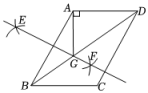 A、6 B、8 C、1 D、18. 如图,已知的顶点 , , 点B在x轴正半轴上,点D在y轴正半轴上,以顶点A为圆心,适当长为半径画弧,分别交 , 于点E,F,再分别以点E,F为圆心,大于的长为半径画弧,两弧交于点M,作射线交于点G.则点G的坐标为( )
A、6 B、8 C、1 D、18. 如图,已知的顶点 , , 点B在x轴正半轴上,点D在y轴正半轴上,以顶点A为圆心,适当长为半径画弧,分别交 , 于点E,F,再分别以点E,F为圆心,大于的长为半径画弧,两弧交于点M,作射线交于点G.则点G的坐标为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 在平行四边形 中, 平分 交边 于 , 平分 交边 于 .若 , ,则 .10. 如图,在▱中,对角线 , 交于点 , , , 过点作的平分线的垂线,垂足为点 , 若点在的垂直平分线上,是直线上的动点,则的最小值为 .
 11. 如图,已知中, , , 两顶点B、D分别在平面直角坐标系的y轴、x轴的正半轴上滑动,连接 , 则线段的最小值是 .
11. 如图,已知中, , , 两顶点B、D分别在平面直角坐标系的y轴、x轴的正半轴上滑动,连接 , 则线段的最小值是 .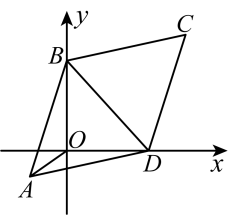 12. 如图,等腰三角形纸片ABC中,于点D , , , 沿AD剪成两个三角形.用这两个三角形拼成平行四边形,该平行四边形较长对角线的长为.
12. 如图,等腰三角形纸片ABC中,于点D , , , 沿AD剪成两个三角形.用这两个三角形拼成平行四边形,该平行四边形较长对角线的长为.
三、解答题
-
13. 如图,在平面直角坐标系中,四边形ABCD是平行四边形,A(-3,0),B(3,0) ,C(0,4),连结OD,点E是线段0D的中点.
 (1)、求点E和点D的坐标.(2)、平面内是否存在一点N,使以C,D,E,N为顶点的四边形是平行四边形?若存在,请求出点N的坐标;若不存在,请说明理由.14. 问题:如图,在平行四边形中, , 的平分线分别与直线交于点E、F.
(1)、求点E和点D的坐标.(2)、平面内是否存在一点N,使以C,D,E,N为顶点的四边形是平行四边形?若存在,请求出点N的坐标;若不存在,请说明理由.14. 问题:如图,在平行四边形中, , 的平分线分别与直线交于点E、F.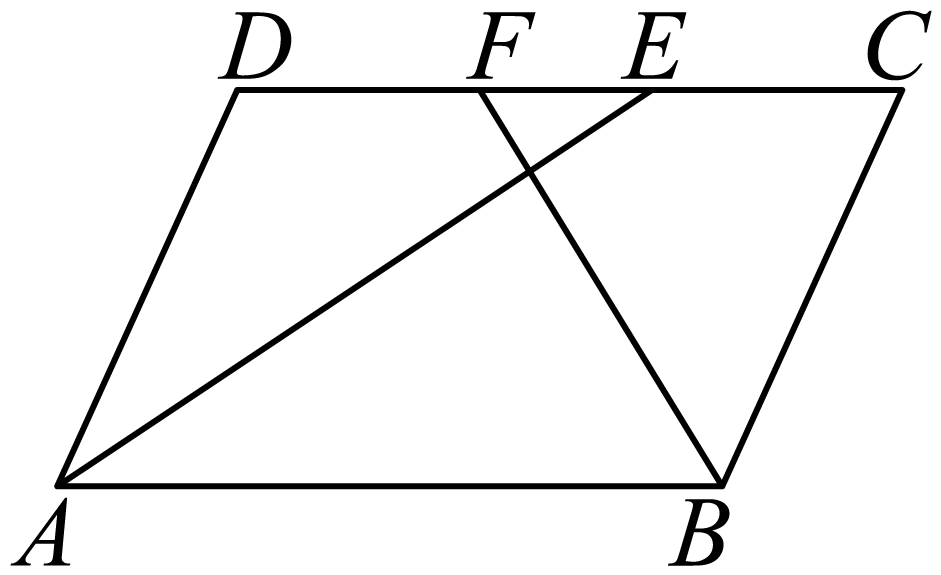 (1)、请直接写出的长.(2)、探究:把“问题”中的条件“”去掉,其余条件不变.
(1)、请直接写出的长.(2)、探究:把“问题”中的条件“”去掉,其余条件不变.①当点E与点F重合时,的长为 .
②当点E与点C重合时,的长为 .
(3)、把“问题”中的条件“”去掉,其余条件不变,当点C , D , E , F相邻两点间的距离相等时,求的值.15. 【综合探究】已知在平面直角坐标系中的位置如图所示,其中边在轴上且 , 边在轴上且 , 平分交于点 . (1)、请直接写出、两点的坐标: , .(2)、如图1,求点的坐标.(3)、过点作交于点 . 如图2,求面积.(4)、在平面内是否存在一点 , 使得、、、四点组成的四边形是平行四边形,若存在,请直接写出点的坐标:若不存在,请说明理由.16. 我们知道平行四边形有很多性质.现在如果我们把平行四边形沿着它的一条对角线翻折.会发现这其中还有更多的结论,如图,已知平行四边形ABCD中,AB=2 , ∠30°,AB≠BC,将△ABC沿AC翻折至△AB′C,连接B′D.
(1)、请直接写出、两点的坐标: , .(2)、如图1,求点的坐标.(3)、过点作交于点 . 如图2,求面积.(4)、在平面内是否存在一点 , 使得、、、四点组成的四边形是平行四边形,若存在,请直接写出点的坐标:若不存在,请说明理由.16. 我们知道平行四边形有很多性质.现在如果我们把平行四边形沿着它的一条对角线翻折.会发现这其中还有更多的结论,如图,已知平行四边形ABCD中,AB=2 , ∠30°,AB≠BC,将△ABC沿AC翻折至△AB′C,连接B′D.
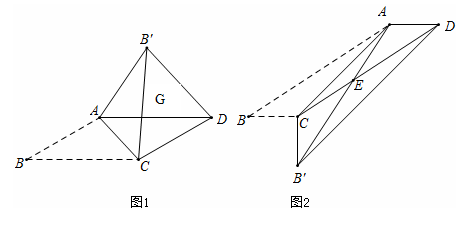 (1)、【发现与证明】
(1)、【发现与证明】如图1:结论①△AGC是等腰三角形;结论②B′D∥AC。请证明结论①或结论②(只需证明一个结论)。
(2)、【应用与解答】如图2:如果BC=1,AB′与CD相交于点E,求△AEC的面积。
(3)、【拓展与探索】直接写出结论,当BC的长为多少时,△AB′D是直角三角形?