贵州省铜仁市印江土家族苗族自治县2023-2024学年八年级下学期3月月考数学试题
试卷更新日期:2024-04-30 类型:月考试卷
一、选择题:(每小题3分,共36分.请将下列各题中唯一正确答案的序号在答题卡中填涂黑.)
-
1. 在中, , , 则的度数是( )A、60° B、30° C、50° D、40°2. 下列条件,不能判定两个直角三角形全等的是( )A、两个锐角对应相等 B、一个锐角和斜边对应相等 C、两条直角边对应相等 D、一条直角边和斜边对应相等3. 下列各组线段长度不能构成直角三角形的一组是( )A、4,5,6 B、3,4,5 C、6,8,10 D、5,12,134. 如图,在中,是斜边上的中线,若 , 则( )
 A、30° B、40° C、50° D、70°5. 如图是某商场一楼与二楼之间的手扶电梯示意图.其中AB、CD分别表示一楼、二楼地面的水平线,∠ABC=150°,BC的长是8 m,则乘电梯从点B到点C上升的高度h是( )
A、30° B、40° C、50° D、70°5. 如图是某商场一楼与二楼之间的手扶电梯示意图.其中AB、CD分别表示一楼、二楼地面的水平线,∠ABC=150°,BC的长是8 m,则乘电梯从点B到点C上升的高度h是( ) A、m B、4 m C、m D、8 m6. 如图,平分 , 于点 , , 是射线上的任一点,则的长度不可能是( )
A、m B、4 m C、m D、8 m6. 如图,平分 , 于点 , , 是射线上的任一点,则的长度不可能是( ) A、4.2 B、5.15 C、3.69 D、87. 如图,以的三边为直角边分别向外作等腰直角二角形.若 , 则图中阴影部分的面积为( )
A、4.2 B、5.15 C、3.69 D、87. 如图,以的三边为直角边分别向外作等腰直角二角形.若 , 则图中阴影部分的面积为( )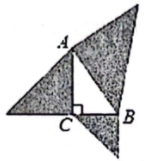 A、 B、 C、 D、58. 如图,五边形的一个内角 , 则等于( )
A、 B、 C、 D、58. 如图,五边形的一个内角 , 则等于( ) A、360° B、290° C、270° D、250°9. 如图,将一副三角板在平行四边形ABCD中作如下摆放,设 ,那么 ( )
A、360° B、290° C、270° D、250°9. 如图,将一副三角板在平行四边形ABCD中作如下摆放,设 ,那么 ( )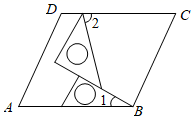 A、 B、 C、 D、10. 如图,在中, , , , 直线垂直平分 , 点为直线上的动点,则的最小值是( )
A、 B、 C、 D、10. 如图,在中, , , , 直线垂直平分 , 点为直线上的动点,则的最小值是( )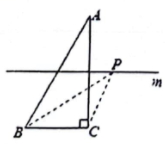 A、1 B、 C、2 D、311. 如图,在中,平分交于点 , 平分交于点 , 若 , , 则的长度为( )
A、1 B、 C、2 D、311. 如图,在中,平分交于点 , 平分交于点 , 若 , , 则的长度为( ) A、4 B、5 C、6 D、712. 如图,在由25个边长为1的小正方形拼成的网格中以为边画 , 使点在格点上,满足这样条件的点共( )个.
A、4 B、5 C、6 D、712. 如图,在由25个边长为1的小正方形拼成的网格中以为边画 , 使点在格点上,满足这样条件的点共( )个.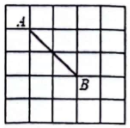 A、5 B、6 C、7 D、8
A、5 B、6 C、7 D、8二、填空题(本大题共4小题,每小题4分,共16分)
-
13. 四边形ABCD中,AD∥BC,要使四边形ABCD成为平行四边形还需满足的条件是(横线只需填一个你认为合适的条件即可)14. 若正多边形的一个内角等于150°,则这个正多边形的边数是15. 在四边形ABCD中,∠A=∠ABC=90°,△BCD为等边三角形,且AD=2,则四边形ABCD的周长为
 16. 如图中, , , 为的中线,点、点分别为线段、上的动点,连接、 , 则的最小值为.
16. 如图中, , , 为的中线,点、点分别为线段、上的动点,连接、 , 则的最小值为.
三、解答题:(本大题共9个小题,第17、18、19、20、21、22题每题10分,第23、24题每小题12分,第25题14分,共98分,要有解题的主要过程)
-
17. 如图,在的正方形网格中,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画满足条件的图形.
 (1)、在图①中,画一个等腰直角三角形,使它的面积是4;(2)、在图②中,画一个平行四边形,使它的面积是6.18. 如图, , 是上的一点,且 , , 求证: .
(1)、在图①中,画一个等腰直角三角形,使它的面积是4;(2)、在图②中,画一个平行四边形,使它的面积是6.18. 如图, , 是上的一点,且 , , 求证: . 19. 已知:如图,四边形是平行四边形,P,Q是对角线上的两个点,且 . 求证: .
19. 已知:如图,四边形是平行四边形,P,Q是对角线上的两个点,且 . 求证: . 20. 如图, , , , , .
20. 如图, , , , , . (1)、求的长;(2)、试判断的形状,并求四边形面积.21. 如图,海中有一小岛 , 它的周围12海里内有暗礁,渔船跟踪鱼群由西向东航行,在处测得小岛在北偏东60°方向上,航行16海里到处,这时测得小岛在北偏东30°方向上.
(1)、求的长;(2)、试判断的形状,并求四边形面积.21. 如图,海中有一小岛 , 它的周围12海里内有暗礁,渔船跟踪鱼群由西向东航行,在处测得小岛在北偏东60°方向上,航行16海里到处,这时测得小岛在北偏东30°方向上. (1)、如果渔船不改变航线继续向东航行,是否有触礁危险,并说明理由;(2)、求点与小落的距离.22. 如图,在△ABC中,∠B=∠C,过BC的中点D作DE⊥AB,DF⊥AC,垂足分别为点E,F.
(1)、如果渔船不改变航线继续向东航行,是否有触礁危险,并说明理由;(2)、求点与小落的距离.22. 如图,在△ABC中,∠B=∠C,过BC的中点D作DE⊥AB,DF⊥AC,垂足分别为点E,F. (1)、求证:DE=DF;(2)、若∠BDE =40°,求∠BAC的度数.23. 如图,点、、、同一条直线上, , , . 求证:
(1)、求证:DE=DF;(2)、若∠BDE =40°,求∠BAC的度数.23. 如图,点、、、同一条直线上, , , . 求证: (1)、;(2)、四边形是平行四边形.
(1)、;(2)、四边形是平行四边形.

