湖南省岳阳市岳阳县九校联考2023-2024学年九年级下学期第一次月考数学试卷
试卷更新日期:2024-04-30 类型:月考试卷
一、单选题
-
1. 的相反数是( )A、 B、2024 C、 D、2. 下列图形中,是轴对称图形但不是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列各式中,计算正确的是( )A、 B、 C、 D、4. 据国家医保局最新消息,全国统一的医保信息平台已全面建成,在全国31个省份和新疆生产建设兵团全域上线,为1360 000 000参保人提供医保服务,医保信息化标准化取得里程碑式突破.数1360 000 000用科学记数法表示为( )A、1.36×107 B、13.6×108 C、1.36×109 D、0.136×10105. 如图,直线直线n , 点A在直线n上,点B在直线m上,连接AB , 过点A作 , 交直线m于点C.若 , 则的度数为( )
3. 下列各式中,计算正确的是( )A、 B、 C、 D、4. 据国家医保局最新消息,全国统一的医保信息平台已全面建成,在全国31个省份和新疆生产建设兵团全域上线,为1360 000 000参保人提供医保服务,医保信息化标准化取得里程碑式突破.数1360 000 000用科学记数法表示为( )A、1.36×107 B、13.6×108 C、1.36×109 D、0.136×10105. 如图,直线直线n , 点A在直线n上,点B在直线m上,连接AB , 过点A作 , 交直线m于点C.若 , 则的度数为( ) A、30° B、40° C、50° D、60°6. 分式方程的解是( )A、x=1 B、x=﹣1 C、x=3 D、x=﹣37. 如图,点 , , 在⊙O上, ,则 的度数为( )
A、30° B、40° C、50° D、60°6. 分式方程的解是( )A、x=1 B、x=﹣1 C、x=3 D、x=﹣37. 如图,点 , , 在⊙O上, ,则 的度数为( ) A、 B、 C、 D、8. 若将点A(1,3)向左平移2个单位,再向下平移4个单位得到点B,则点B的坐标为( )A、(﹣1,0) B、(﹣1,﹣1) C、(﹣2,0) D、(﹣2,﹣1)9. 如图,Rt△ABC中,∠C=90°,∠B=30°,分别以点A和点B为圆心,大于 的长为半径作弧,两弧相交于M、N两点,作直线MN , 交BC于点D , 连接AD , 则∠CAD的度数是( )
A、 B、 C、 D、8. 若将点A(1,3)向左平移2个单位,再向下平移4个单位得到点B,则点B的坐标为( )A、(﹣1,0) B、(﹣1,﹣1) C、(﹣2,0) D、(﹣2,﹣1)9. 如图,Rt△ABC中,∠C=90°,∠B=30°,分别以点A和点B为圆心,大于 的长为半径作弧,两弧相交于M、N两点,作直线MN , 交BC于点D , 连接AD , 则∠CAD的度数是( )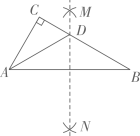 A、20° B、30° C、45° D、60°
A、20° B、30° C、45° D、60°二、多选题
-
10. 如图,抛物线与x轴交于点 , 则下列结论中正确的是( )
 A、 B、 C、 D、
A、 B、 C、 D、三、填空题
-
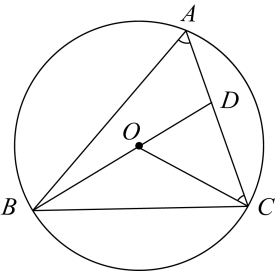
11. 在 中无理数的个数是个.12. 若二次根式有意义,则实数x的取值范围是.13. 抛物线y=3(x﹣2)2+5的顶点坐标是 .14. 若关于 的方程 的一个根为3,则 的值为.15. 如图所示,点A、B、C是上不同的三点,点O在的内部,连接、 , 并延长线段交线段于点D.若 , 则度.
 16. 如图,在 中, , 平分 交 于点 , ,垂足为 ,若 , ,则 的长为.
16. 如图,在 中, , 平分 交 于点 , ,垂足为 ,若 , ,则 的长为.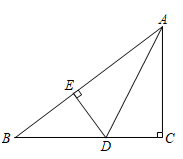 17. 不等式组的所有整数解的和是 .18. 若关于x的方程恰有三个根,则t的值为.
17. 不等式组的所有整数解的和是 .18. 若关于x的方程恰有三个根,则t的值为.四、解答题
-
19. 计算:.20. 先化简,再求值: ,其中a=2,b= .21. 如图,已知反比例函数 与正比例函数 的图象交于 , 两点.
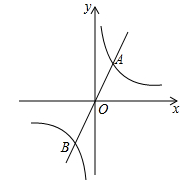 (1)、求该反比例函数的表达式;(2)、若点 在 轴上,且 的面积为3,求点 的坐标.22. 近年,“青少年视力健康”受到社会的广泛关注.某校综合实践小组为了解该校学生的视力健康状况,从全校学生中随机抽取部分学生进行视力调查.根据调查结果和视力有关标准,绘制了如下两幅不完整的统计图.请根据图中信息解答下列问题:
(1)、求该反比例函数的表达式;(2)、若点 在 轴上,且 的面积为3,求点 的坐标.22. 近年,“青少年视力健康”受到社会的广泛关注.某校综合实践小组为了解该校学生的视力健康状况,从全校学生中随机抽取部分学生进行视力调查.根据调查结果和视力有关标准,绘制了如下两幅不完整的统计图.请根据图中信息解答下列问题: (1)、所抽取的学生人数为;(2)、补全条形统计图,并求出扇形统计图中“轻度近视”对应的扇形的圆心角的度数;(3)、该校共有学生3000人,请估计该校学生中近视程度为“轻度近视”的人数.23. 某镇为创建特色小镇,助力乡村振兴,决定在辖区的一条河上修建一座步行观光桥,如图,该河旁有一座小山,山高 ,坡面 的坡度 (注:从山顶 处测得河岸 和对岸 的俯角分别为 , .
(1)、所抽取的学生人数为;(2)、补全条形统计图,并求出扇形统计图中“轻度近视”对应的扇形的圆心角的度数;(3)、该校共有学生3000人,请估计该校学生中近视程度为“轻度近视”的人数.23. 某镇为创建特色小镇,助力乡村振兴,决定在辖区的一条河上修建一座步行观光桥,如图,该河旁有一座小山,山高 ,坡面 的坡度 (注:从山顶 处测得河岸 和对岸 的俯角分别为 , .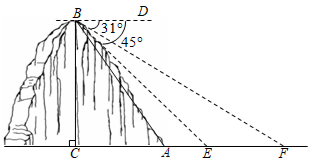
(参考数据: , , )
(1)、求山脚 到河岸 的距离;(2)、若在此处建桥,试求河宽 的长度.(结果精确到 )24. 如图,AB与⊙O相切于点C,OA,OB分别交⊙O于点D,E, =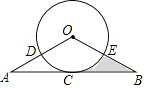 (1)、求证:OA=OB;(2)、已知AB=4 ,OA=4,求阴影部分的面积.25. 已知抛物线与轴相交于点 , , 与轴相交于点 .
(1)、求证:OA=OB;(2)、已知AB=4 ,OA=4,求阴影部分的面积.25. 已知抛物线与轴相交于点 , , 与轴相交于点 . (1)、求抛物线的表达式;(2)、如图1,点是抛物线的对称轴上的一个动点,当的周长最小时,求的值;(3)、如图2,取线段的中点 , 在抛物线上是否存在点 , 使?若存在,求出点的坐标;若不存在,请说明理由.26. 在直角坐标系中,我们不妨将横坐标,纵坐标均为整数的点称之为“中国结”.(1)、求函数y=x+2的图像上所有“中国结”的坐标;(2)、求函数y=(k≠0,k为常数)的图像上有且只有两个“中国结”,试求出常数k的值与相应“中国结”的坐标;(3)、若二次函数y=(k为常数)的图像与x轴相交得到两个不同的“中国结”,试问该函数的图象与x轴所围成的平面图形中(含边界),一共包含有多少个“中国结”?
(1)、求抛物线的表达式;(2)、如图1,点是抛物线的对称轴上的一个动点,当的周长最小时,求的值;(3)、如图2,取线段的中点 , 在抛物线上是否存在点 , 使?若存在,求出点的坐标;若不存在,请说明理由.26. 在直角坐标系中,我们不妨将横坐标,纵坐标均为整数的点称之为“中国结”.(1)、求函数y=x+2的图像上所有“中国结”的坐标;(2)、求函数y=(k≠0,k为常数)的图像上有且只有两个“中国结”,试求出常数k的值与相应“中国结”的坐标;(3)、若二次函数y=(k为常数)的图像与x轴相交得到两个不同的“中国结”,试问该函数的图象与x轴所围成的平面图形中(含边界),一共包含有多少个“中国结”?
-